Constructii geometrice cu rigla si compasul - constructii MOHR- MASCHERONI

Dintre toate problemele de geometrie problemele de constructii geometrice sunt acelea care stimuleaza in gradul cel mai inalt spiritul de observatie, de claritate si de logica.

Problemele de constructii cu rigla si compasul exercita spiritul in directia creatoare, inventiva folosind materialul teoretic invatat.

Problemele de constructii geometrice pe langa faptul ca sunt atractive au si o influenta binefacatoare asupra judecatii rezolvitorului, pentru ca in ele se canalizeaza, se repeta si se retine mai bine materia invatata si in acelasi timp se pot descoperi proprietati noi, dand prin aceasta incredere in puterea creatoare a rezolvitorului.

Manualele de geometrie contin un numar mic de aplicatii la acest capitol fapt pentru care elevii trec cu usurinta peste aceste probleme, iar la diferitele concursuri si olimpiade scolare intampina greutati in rezolvarea problemelor de acest gen

Etape de rezolvare

In general in cadrul unei probleme de constructie se evidentiaza patru etape iar continutul lor il voi descrie succesiv dupa cum urmeaza:

I Analiza - incepe de obicei prin fraza ,,presupune problema rezolvata''. In cadrul acestei etape, pe o figura de obicei aproximativa consideram simultan datele (elementele lui D) si necunoscutele (apartinand lui X ). Se adauga figuri elemente noi (constructii ajutatoare) caracterizate prin proprietatile lor referitoare la elementele din DUX, alcatuind o multime A. Se pun apoi in evidenta proprietati definitorii ale elementelor din A ce folosesc doar elemente din D si proprietati definitorii pentru elementele lui X formulate cu ajutorul elementelor din D si A.

II Constructia sau sinteza exprima succesiuni de utilizari ale elementelor permise pentru a trasa elementele din A si apoi din X. Aceasta etapa constituie in fond ,,o reteta de fabricare'' a elementelor din X. Uneori se manifesta tendinta de a da numai aceasta etapa in problemele de constructie, ceea ce este gresit, deoarece geometria contemporana nu rezida in retete.

III Demonstratia sau justificarea contine argumentarea faptului ca elementele construite satisfac proprietatile enuntate; prin intermediul acestei etape problemele de constructie isi justifica incadrarea in probleme de geometrie si nu de desen liniar.

IV Discutia pune in evidenta conditii asupra datelor problemei pentru ca sa existe solutii si o estimare a numarului de solutii. In cadrul acestei etape sunt justificate si generalizari sau analogii ale problemei. In general, discutia este conturata prin analiza critica a fiecarei operati descrise in etapa de constructie.

Constructii fundamentale

Se considera urmatoarele operati numite constructii geometrice fundamentale:

1. Trasarea unei drepte cu rigla cand se cunosc doua puncte distincte care ii apartin.

2. Determinarea punctului de intersectie a doua drepte date.

3. Trasarea cu compasul a unui cerc cand este dat centru si un segment a carui lungime este raza.

4. Determinarea punctelor de intersectie dintr-o dreapta si un cerc.

5. Determinarea punctelor de intersectie a doua cercuri.

6. Constructia unui segment congruent cu un segment dat (existenta si unicitatea solutiei rezulta din teorema de constructie a unui segment).

7 Constructia unui segment congruent cu suma sau diferenta a doua segmente (in baza teoremei de adunare si scadere a segmentelor).

8. Simetricul unui punct fata de un alt punct (si a punctelor echidistante).

9 Constructia mediatoare a unui segment (AB) se poate face imediat dupa definirea ei la loc geometric

M

A B

N

Constructia : fie segmentul ( AB)                              

C₁ construim cercul C(A, R), R > AB/2.

C₂ construim cercul C( B, R), si notam intersectia celor doua cercuri cu M si N.

C₃ construim dreapta MN.

Demonstratia: punctele M si N sunt egal departate de A si B deci apartin mediatoarei segmentului (AB) iar doua puncte distincte determina o dreapta.

Observatie : aceasta constructie se foloseste si la:

a)      aflarea mijlocului unui segment care este dat de intersectia mediatoare cu segmentul.

b)      constructia unui cerc de diametru dat.

c)      constructia cerului circumscris unui triunghi ( centru cercului fiind dat de punctul de intersectie a mediatoarelor laturilor triunghiului.

d)      impartirea unui segment in 2ⁿ segmente congruente.

10. Constructia bisectoarei interioare unui unghi XOY

Constructia: fie unghiul XOY

C₁ construim cercul C(O , R) care intersecteaza (OX si (OY in A si B

C₂ construim cercurile C (A ,R^{`</sup>) si C ( B , R<sup>`}) si alegem unul din punctele lor de intersectie si il notam cu M

C₃ construim semidreapta ( OM

(OM - este bisectoarea unghiului XOY

Y

M

O

X

Demonstratie: D OAC s D OBC ( L.L.L.) rezulta ca AOC s BOC deci (OM este bisectoarea XOY.

Observatie: aceasta constructie se foloseste la:

a)      impartirea unui unghi in 2ⁿ unghiuri congruente sau cand vrem sa determinam un unghi a carui masura sa fie 1/2ⁿ din masura unui unghi dat.

b)      constructia cercului inscris in triunghi (centrul cercului fiind dat de intersectia bisectoarelor unghiurilor triunghiului.

11. Constructia perpendicularei prin A pe o dreapta d.

Constructia: (solutia 1 )

C₁ construim cercul C(A, R) care taie dreapta d in B si B^`

C₂ construim mediatoarea segmentului (B B^`)

A

d

B B^`

Constructia: (solutia 2) pentru cazul particular A I d putem da

si urmatoarea solutie. Fie B I d

C₁ construim C(A, r)

C₂ construim C (B, r) si notam intersectia celor doua cercuri cu M

C₃ construim P I (BM astfel incat (BM) s (M P)

C₄ construim dreapta AP

Demonstratia: mediana AM are lungimea egala cu jumatatea lungimi laturi opuse deci D ABP este dreptunghic cu m ( A) = 90⁰ .

Observatie: acest rezultat il putem utiliza in construirea unui unghi drept sau a unui unghi a carui masura sa fie dintr-un unghi drept.

12. Constructia unui unghi ce are o latura O^{`</sup>X<sup>`} si este congruent cu unghiul XOY .

Constructia:

C₁ construim cercul C(O,R) care taie (OX si (OY in AB

C₂ construim C( O^{`</sup> , R) care taie (O<sup>`} X^{`</sup> in A<sup>`}

C₃ construim C(A^{`</sup> , AB) si notam C(O<sup>`} , R) C(A` , AB) = =

C₄ construim semidreapta (O`B`

Unghiul A`O`B` este unghiul cautat.

Demonstratia: DAOBsDA`O`B` (L.L.L.)

Discutia: Cercul C(A`,AB) este secant cercului C(O`,R) deoarece R-AB <O`A`=R<R+AB deci cele doua cercuri se taie in doua puncte. Problema admite doua solutii semidreptele (OB` si (OB`` fiind in semiplane distincte limitate de dreapta O`A`.

Observatie: Acest rezultat se poate folosi in construirea unui unghi de masura egala cu suma sau diferenta masurilor a doua unghiuri date. De asemenea in baza axiomei de congruenta L.U.L. putem construi un triunghi cunoscand un unghi si laturilor alaturate lui

O alta aplicatie directa a acestei probleme ar fi constructia unui triunghi cunoscand o latura si unghiurile alaturate ei (vezi teorema de congruenta U.L.U.).

Mai putem construi complementul si suplementul unui unghi.

13.Constructia paralelei prin A la d.

Analiza: Presupunem problema rezolvata; fie d` paralela prin A la d si fie B,C pe d, D pe d` astfel incat C, D` sa fie parti distincte ale dreptei AD. Va avea loc ABCs BAD Constructia: fie B,C pe d

C₁ Construim (AD astfel incat ABCs BAD

A D

d

d C B

Discutia: Constructia relatata nu cuprinde cazul AId, in acest caz d`= d

Solutia este unica (vezi axioma paralelelor)

Constructii cu ajutorul compasului (constructii MOHR- MASCHERONI)

1. Constructia simetricului unui punct si a simetricului unui cerc fata de o dreapta.

Se da un cerc cu centrul C si o dreapta data prin punctele D₁ si D₂ Construim cercurile care trec prin C si au centrele in D₁ respectiv D₂. Aceste doua cercuri se mai taie in punctul C`. Se observa ca C` este tocmai simetricul punctului C fata de dreapta D₁ D₂ iar cercurile cu centrele in C si C` si de raze egale sunt de asemenea simetrice fata de aceeasi dreapta

2. Constructia multiplului unui segment.

Fie A₁ O data prin punctele A₁ si O. Ducem cercul cu centrul in O si avand raza A₁ O. Pornind din A₁ masuram pe acest cerc de trei ori consecutiv cate o coarda de lungimea razei si obtinem punctul A₂. Punctul A₂ este pe dreapta A₁ O si A₁ A₂ = 2A₁ O. Pornind de la segmentul O A₂ si repetand constructia precedenta obtinem punctul A₃ care este tot pe dreapta A₁ O si A₁ A₃ = 3A₁ O. s.a.m.d.

Proiect: Transformarea energiei de oxido-reducere in bioluminiscenta Referat: Legile fundamentale ale chimiei

3. Constructia mijlocului unui segment

Fie A si B doua puncte distincte.

C₁ Construim cercul C(B,AB)

C₂ Construim hexagonul regulat ABCDEF inscris in cercul C(B,AB), unde l₆=AB

C₃ Construim cercurile C(E,EA) si C(A,AB) a caror intersectie o notam cu H si I

C₄ Construim cercurile C(H,AB) si C(I,AB) a caror intersectie o notam cu A si M.

Punctul M se afla la mijlocul segmentului (AB).

Demonstratie: Triunghiurile isoscele AHM si AEH avand unghiul comun A sunt asemenea de unde rezulta:

si obtinem AM=

Observatii: a) Asa cum s-a construit mijlocul M al segmentului (AB) se poate construi mijlocul M` a lui (AM), mijlocul M`` a lui (AM`) deci se poate construi punctul M_n cu proprietatea AM_n=

b)Dupa cum rezulta din constructie se vede ca nu este neaparata nevoie ca segmentul (AB) sa fie desenat.

Constructii cu rigla

Sa analizam constructiile care pot fi facute numai cu rigla:

1. Daca este dat un singur punct sau o singura dreapta, pornind de la acestea, nu putem construi un alt punct sau o alta dreapta. Nu gasim perechi de puncte la care, potrivita rigla, am putea trasa drepte noi.

2. Daca sunt date doua puncte putem trasa dreapta care trece prin ele si nimic mai mult.

3. Daca sunt date doua drepte putem construi punctul lor de intersectie.

4. Daca sunt date trei puncte, putem construi triunghiul determinat de ele, sau putem trasa dreapta pe care se gasesc ele. In cazul a trei drepte rationam la fel.

5.In cazul a patru puncte dam de constructii mai interesante. Fie patru puncte date dispuse arbitrar A,B,C,D(trei din ele sa nu fie coliniare).In acest caz putem construi de pilda punctul E, intersectand dreptele AB si CD .Avem deci trei puncte pe o dreapta A,E,B si doua puncte in afara dreptei, C si D. Pe aceasta dreapta putem construi, numai cu rigla, un al patrulea punct F in asa fel ca punctele A,E,B,F, sa formeze un biraport armonic. Construirea acestui punct ne este cunoscuta din geometria proiectiva si se bazeaza pe proprietatile armonice ale patruunghiului complet. (pe fiecare diagonala a patruunghiului complet exista un grup armonic de puncte format din cele doua puncte diagonale si punctele de intersectie ale acestei diagonale cu perechea de laturi care trec prin al treilea punct diagonal s.a.)

Ea se efectueaza trasand dreptele numerotate ordinea de succesiune indicata de acele numere.

6.Sa se construiasca cu rigla mijlocul segmentului (AB) dandu-se o dreapta paralela cu AB.

Analiza: Fie M,NId

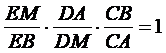
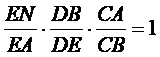
dar si

T (AC)s(BC)                                                   

Constructia: Fie M , N doua puncte oarecare pe dreapta d

C₁. Construim dreptele AN si BM si notam intersectia lor cu E

C₂. Construim dreptele AM si BN si notam intersectia lor cu D

C₃. Construim dreapta ED si notam intersectia ei cu dreapta AB cu C

Punctul C este solutia problemei

Demonstratia: rezulta din analiza problemei

Constructii cu rigla, fiind desenat un cerc impreuna cu centrul sau

(constructii PONCELET-STEINER)

Poncelet si independent de el, Steiner au gasit urmatoarea teorema:

Daca pe foaia de desen avem desenat un cerc si centrul sau, putem efectua numai cu rigla toate constructiile efectuabile cu rigla si compasul.

Sa consideram un cerc si centrul sau O. Putem desena o dreapta daca este dat inca un punct P. Obtinem puncte noi taind punctul fix cu dreapta .Dreapta OP taie cercul in doua puncte . Pentru a obtine alte puncte, avem nevoie de inca un punct Q in afara dreptei OP. Putem duce o paralela la OP, caci punctul O imparte diametrul in doua parti egale. Ducem dreapta QO si din unul dintre punctele ei de intersectie cu cercul ducem o paralela la OP. Gasim mijlocul coardei astfel obtinute, unim mijlocul sau cu punctul O si am obtinut un diametru perpendicular pe primul diametru. Aceste diametre determina un patrat ale carui laturi sunt egale cu raza cercului. In acest caz consideram ca axele de coordonate coincid cu cele doua diametre perpendiculare.

Constructii geometrice utilizand alte instrumente

Constructii cu echerul Cu ajutorul echerului dreptunghic pot fi construite dreptunghiuri si oricate puncte ale unui cerc dat printr-un diametru. Toate constructiile care pot fi efectuate cu rigla, fiind desenat un paralelogram si mai multe unghiuri drepte, evident pot fi rezolvate numai cu echerul.

Cu ajutorul echerului putem construi punctele de intersectie ale unei drepte d cu un cerc dat prin centrul O si un punct P de pe cerc. Construim diametrul PP`. Deplasand varful echerului pe dreapta d, pentru ca totodata una dintre laturi sa treaca prin punctul P. La un moment dat cealalta latura trece prin punctul P`. In acest moment varful echerului este pe cerc si indica tocmai punctul de intersectie al dreptei d cu cercul. (determinarea acestui punct nu poate fi numita constructie geometrica ci un experiment)

a)multiplicarea si impartirea segmentelor.Fie segmentul (AB). Ducem o dreapta oarecare d prin A si o perpendiculara prin B. In punctul lor de intersectie ridicam o perpendiculara pe d si in punctul A o alta perpendiculara tot pe d care taie insa perpendiculara ridicata in B. In M ridicam o perpendiculara pe AM s.a.m.d

b)Sa se construiasca centrul cercului circumscris triunghiului ABC.Ridicam perpendiculara in A pe AC si in B pe BC, care se taie in D. Dreapta care uneste punctele C si D trece prin centrul cercului circumscris, prin O.

Metode de rezolvare a problemelor de constructie.

Referitor la metodele de rezolvarea a problemelor de constructii este imposibil sa se dea sau cel putin sa se indice o metoda generala si sigura pentru a rezolva toate problemele de constructii geometrice sau cel putin o parte din ele.

Metodele generale intrebuintate in rezolvarea problemelor de constructie geometrica sunt analiza si sinteza.

Analiza: este o metoda prin care o proprietate necunoscuta se aduce la o alta proprietate necunoscuta, aceasta la o a treia si asa mai departe pana se ajunge la o proprietate evidenta.

Intre proprietatea initiala si cea finala se pot intercala mai multe proprietati intermediare.

Exemplu: Sa se construiasca un triunghi ABC in care se cunosc:

AC+BA = m, BC = a si m ( B) < 90⁰ (manualul de clasa a VI)

Analiza: presupunem problema rezolvata si fie triunghiul ABC in care avem AC +BA = m, BC = a , m( B) < 90⁰ de masura data .

Se prelungeste latura BA cu un segment (AD )s (AC) pentru a pune in evidenta segmentul BD = m si se aduce problema la construirea D BCD in care se cunoaste masura unghiului B latura BC = a si latura BD = m.Problema s-a adus la alta mai simpla si foarte cunoscuta: construirea unui triunghi cand se cunosc doua laturi si unghiul cuprins intre ele. Acum se observa ca triunghiul ACD este isoscel pentru ca (AD) s (AC) rezulta ca ADC s DCA sau daca construim AE DC rezulta ca (CE) s (ED).

Constructia : fie xBY unghiul dat.

C₁ se construieste C I (BX astfel incat BC = a

C₂ construim D I (BY astfel incat BD = m

C₃ construim triunghiul BDC

C₄ construim mediatoarea laturi DC si notam d BD =

C_4` sau construim (Cz int BCD astfel incat DCZ s BDC si notam (Cz BD =

C₅ construim triunghiul ABC

Demonstratie: BC = a si BD =m (din constructie)

Triunghiul ACD este isoscel rezulta ca (AC) s (AD) rezulta ca AB +AC= m

Discutie: constructia este posibila si are solutie unica daca m > a, adica

AB +AC > BC.

Sinteza pleaca de la o proprietate cunoscuta, la o alta cunoscuta, de la aceasta la o a treia s.a.m.d pana se ajunge la problema propusa initial. Astfel in exemplu precedent putem construi triunghiul BDC dandu-se unghiul B si laturile BC = a, BD = a. Se cere in continuare sa determinam un punct A I BD astfel incat AB +AC = m sau BD = AD +AB = m T (AC) s (AD), deci am transformat problema in ,,construirea unui triunghi isoscel ADC cunoscand latura DC si un unghi de al baza,

ADC''. Acest lucru se poate rezolva in doua moduri:

a)      construind mediatoarea laturi DC.

b)      construind ACD s BCD, ambele probleme cunoscute

In cadrul acestor metode generale de analiza si sinteza sunt

numeroase metode particulare dintre care unele sunt enumerate in cele ce urmeaza:

Metoda substitutiilor succesive se aduce problema data la o alta care la randul ei se aduce la o a treia s.a.m.d . pana se ajunge la o constructie cunoscuta sau la una a carei solutie este imediata.

Astfel, de exemplu: ,,sa se construiasca tangentele comune la doua cercuri date" Se aduce constructia tangentei dintr-un punct exterior la o circumferinta (fig.3.1.2)

OT>O`T`, OT MT, O`T` MT`T OT || O`T`T D MO`T`~ D MOTT

sau

Determinarea punctului M este tratata la construirea unui segment (a patra proportionala a segmentelor a, b, c,)

Stiind ca m ( MTO ) = 90⁰, locul geometric al punctelor T pentru care m ( MTO) =90⁰, unde M si O sunt date se afla pe cercul de diametru OM. Intersectia cercului C (O, r) cu cercul C (O₁ , ) o notam cu T si T₁. Dreptele M T si MT₁ sunt o parte din solutiile problemei, adica tangentele exterioare.

In mod analog se procedeaza si pentru tangentele interioare.

Metoda prin intersectii de locuri geometrice.

Unele probleme de constructii geometrice se reduc la determinarea unui punct care indeplineste anumite conditii. Metoda determinarii acelui punct prin intersectii de locuri geometrice consta in a nu-l lua in seama decat una din conditii si a cauta locul geometric al punctelor care indeplinesc aceasta conditie. De exemplu: ,,constructia cercului circumscris unui triunghi ABC se reduce la constructia centrului care se gaseste la egala distanta fata de varfurile triunghiului dat''.

Daca luam doua varfuri ale triunghiului A si B locul geometric al punctelor egal departate de capetele unui segment este mediatoarea segmentului. Acesta este primul loc geometric al punctului cautat. daca luam in considerare alte doua varfuri de exemplu B si C punctul O este egala departat si de aceste doua puncte, deci se afla pe mediatoarea segmentului (BC).

Intersectia celor doua locuri geometrice ne da punctul cautat. Exista si alte metode de rezolvare a problemelor de constructii geometrice printre acestea numarandu-se si metoda algebrica sau prin relatii metrice.

Metoda aceasta este foarte fecunda si se poate aplica oricarei probleme de geometrie dar in acest caz dispare eleganta solutiei geometrice. Metoda consta in a stabili relatii metrice intre elementele cunoscute si elementul sau elementele necunoscute; uneori se stabilesc ecuatii sau sisteme de ecuatii care se rezolva dupa metode date de algebra. Necunoscutele apar sub forma unor expresii algebrice sau numerice care se construiesc apoi geometric. O alta metoda foarte des utilizata in rezolvarea problemelor de constructie cu rigla si compasul este problematizarea si invatarea prin descoperire.

Astfel in problema: ,,construiti bisectoarea unghiului A a triunghiului ABC fara sa trasati laturile triunghiului ABC'', notiunea de bisectoare si proprietatile ei, considerate ca loc geometric reprezinta un sistem ineficient ,operational si pretinde completarea informatiei cu proprietatea ,,arcul BC subintins de unghiul A, apartinand cercului circumscris triunghiului ABC este impartit de bisectoarea unghiului A in doua arce congruente.

In problemele de constructii cu rigla si compasul demonstratia apare ca o etapa distincta de rezolvare ceea ce nu exclude folosirea ei si in alte etape.

PROBLEME PROPUSE

Se dau segmentele a,b,c,. Se cere sa se construiasca un segment x egal

cu .

Constructia: fie unghiul XOY un unghi oarecare

C₁ construim A I (OX astfel incat OA = a

C₂ construim B I (OX astfel incat OB = b

C₃ construim C I (OY astfel incat OC = c

C₄ construim (Bz astfel incat Bz|| AC si notam (Bz (OY = segmentul OD ne da solutia problemei

Demonstratie:

Observatie: daca b =c T .

Fie segmentele (AB) si (CD) cu AB = a, CD = b, a > b. Sa se construiasca un segment de lungime .

Solutie - aplicam teorema inaltimii

Constructia:

C₁ construim segmentul AB = a +b cu D I (AB), AD = a, DB = b.

C₂ construim cercul de diametru AB

C₃ construim d AB, D I d. Alegem unul din punctele de intersectie a dreptei d cu cercul si-l notam cu C

C₄ construim segmentul (CD)

Demonstratie: AD = a, DB = b, (din constructie). Triunghiul ACB dreptunghic m ( C) = 90⁰ T CD AB. Aplicand teorema inaltimi obtinem CD² = AD DB = a b, T CD = .

Sa se construiasca segmentele AB si CD astfel incat sa avem , m si n fiind segmente de lungimi date.

Analiza: consideram triunghiul dreptunghic ale carei catete sunt respectiv

NM = m si NP = n. Construim NQ MP, QR MN, QS NP.

( 1)

MN² = MQ MP, PN² = RQ PM (2)

Deci segmentele cautate sunt: AB = l MR, CD = l PS.

Constructia:

C₁ construim triunghiul MNP dreptunghic cu m ( N) = 90⁰,

cu MN = m , NP = n.

C₂ construim NQ MP

C₃ construim QP MN

C₄ construim QS NP

Segmentele MR si PS sau multiplii ai acestora sunt segmentele cautate AB si CD.

Prin punctul P sa se construiasca secanta PAB la laturile unghiului xOy asa incat P sa fie mijlocul segmentului (AB).

Analiza: fie unghiul xOy, PIint xOy.

Construim PM (Oy, MI(Ox, AI(Ox , (OM)s(MA), AP (Oy =

Avem MP linie mijlocie in DAOB, T (AP)s(BP)

Constructia:C₁ construim Pz (Oy si notam Pz (Ox=

C₂ construim cercul C(M,OM) care intersecteaza (Ox in A C₃construim dreapta AP care intersecteaza (Oy in B

Dreapta AB este solutia problemei.

Discutia: problema are solute unica pentru PIint xOy ,in caz contrar problema nu are solutie.

.Impartirea unui segment in n parti congruente. (caz particular n=5)

Constructia: fie segmentul AB=u

C₁ construim semidreapta (Ax,

C₂ construim A_iI(Ax , i=1,5 astfel incat AA₁=A₁A₂=A₂A₃=A₃A₄=A₄A₅=n C₃ construim A₅B

C₄ construim A_iB_i A₅B , B_iIAB, i=1,4

Punctele B_i sunt cele cautate.

Demonstratia : din A_iB_i || A₅B obtinem:

(1)

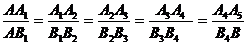
iar in baza relatiei (1) obtinem :

(AB₁)s(B₁B₂)s(B₂B₃)s(B₃B₄)s(B₄B)

Impartirea unui segment intr-un raport dat k (kIQ

Caz particular .

Analiza : CE || BD rezulta

Constructia: se da segmentul AB ; fie segmentul MN=u

C₁ construim semidreapta (Ax

C₂ construim CI(Ax ,astfel incat AC=3u

C₃ construim DI(Ax ,astfel incat AD= 8u

C₄ construim BD

C₅ construim (Cy|| BD si notam (Cy AB

Demonstratia : CE||BD

. Constructia unui arc capabil de un unghi dat.

Se dau: punctele A si B si unghiul u mai mic de 180⁰.

Se cere: sa se construiasca arcul capabil de unghiul u cu capetele in A si B (in unul din semiplanele limitate de dreapta AB.

Analiza: presupunem problema rezolvata u+v+w=180⁰

Daca consideram aceste unghiuri fiind unghiurile de la baza triunghiului isoscel ABM .

Constructia : fie m( CDE)=u⁰

C₁ construim EDC`=180⁰-u

C₂ construim bisectoarea (DF a unghiului EDC`T

EDFs FDC`=;

C₃ construim (Ax astfel incat m( BAX=<90⁰

C₄ construim (By astfel incat m( ABY)=<90⁰ (BY este situata in acelasi semiplan fata de dreapta AB ca si (Ax.

C₅ notam (Ax (By=

C₆ construim cercul circumscris triunghiului AMB.

Arcul AB este arcul capabil de unghiul u.

Discutia: problema admite o singura solutie abstractie facand de simetricul arcului AB in raport cu dreapta AB.

Constructii de poligoane regulate

K. Gauss a demonstrat posibilitatea construirii cu rigla si compasul a poligoanelor regulate cu p laturi, p-numar prim numai in cazul numerelor de forma .

1. Se da: cercul C(O,R)

Se cere: sa se construiasca patratul si octogonul regulat inscris in cerc. (impartirea cercului in patru respectiv in opt arce congruente).

Analiza: Intru-un patrat diagonalele sunt congruente si perpendiculare.

Constructia:

C₁ construim diametrul AC

C₂ construim mediatoarea segmentului (AC) si notam:

d C(O,R)=

Patrulaterul ABCD este un patrat.

C₃ construim d₁ bisectoarea AOB, si notam: d₁ C(O,R)=

C₄ construim d₂ bisectoarea BOC, si notam: d₂ C(O,R)=.

Poligonul AEBFCGDH este un octogon .

Se da cercul C(O, R). Se cere sa se construiasca triunghiul echilateral si hexagonul regulat, inscrise in cerc. (impartirea cercului in trei, respectiv sase arce congruente).

Analiza: Latura hexagonului regulat este egala cu raza cercului circumscris.

Constructia :

C₁ construim cercul C(A,R) si notam: C(A,R) C(O,R)=

C₂ construim C(B,R) C(O,R)=

C₃ construim C(C,R) C(O,R)=

C₄ construim C(D,R) C(O,R)=

Poligonul ABCDEF este hexagonul regulat inscris in cerc (l₆=R), iar triunghiul ACE este triunghiul echilateral inscris in cerc.

Se da cercul C(O,R). Se cere sa se construiasca pentagonul si decagonul regulat inscrise in cerc (impartirea unui cerc in cinci si zece arce congruente).

Constructia :

C₁ construim doua diametre perpendiculare AB CD

C₂ construim C(A,R) C(O,R)=

C₃ construim EF AB

C₄ construim C(M,MC) AB=

Segmentul (CN) este latura pentagonului , iar segmentul (ON) este latura decagonului inscris in cerc

Repetand procedeul de la problema precedenta , luand ca raza segmentele (CN) respectiv (ON), obtinem pentagonul respectiv decagonul inscris in cerc.

Demonstratie: CM=

ON=MN-OM=

CN=

BIBLIOGRAFIE

A.I.Alexandrov                                   Probleme de constructii geometrice ; Editura Tehnica, Bucuresti , 1951.

2. Gh. Buicliu       Probleme de constructii geometrice cu rigla si compasul; Editura tehnica, Bucuresti, 1957.

3. A.N. Kolmogrov                                 Geometria pentru clasele I-VIII(traducere din limba rusa); Editura didactica si pedagogica, Bucuresti, 1979

4. Edwin E. Moise                                 Geometrie; Editura didactica si pedagogica

Floyd L. Downe Jr. Bucuresti ,1983

5. Augustin Cota  Matematica-Geometrie si trigonometrie.

M. Radutiu Manual pentru clasa a-IX-a; Editura

Marta Rado didactica si pedagogica, Bucuresti 1984

6. I. Rus, D. Varna                                 Metodica predarii matematicii; Editura didactica si pedagogica, Bucuresti,1983

7. Olimpia Popescu Metodica predarii geometriei in gimnaziu

V. Radu Editura didactica si pedagogica, Bucuresti, 1983.

8. Gh. A. Chitei    Metode pentru rezolvarea problemelor de geometrie; Editura didactica si pedagogica Bucuresti, 1969.

9. G. Polya Cum rezolvam o problema; Editura stiintifica, Bucuresti, 1965.

10. I. Cuculescu   Matematica-geometrie; Editura didactica si

C. Ottescu pedagogica, Bucuresti, 1979, manual pentru clasa a-VI-a.

11. I. Cuculescu   Matematica-geometrie; Editura didactica si

C. Ottescu pedagogica, Bucuresti, 1980, manual pentru clasa a-VII-a.

12. Al. Toth          Notiuni de teoria constructiilor geometrice; Editura didactica si pedagogica, Bucuresti, 1963.