
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Miscarea oscilatorie amortizata |
Miscarea oscilatorie amortizata
Miscarea oscilatorie amortizata
O miscare oscilatorie a carei amplitudine scade in timp se numeste miscare oscilatorie amortizata. Amortizarea miscarii se datoreaza unor forte disipative de energie, cum ar fi, de exemplu, fortele de frecare. Acestea transforma treptat energia sistemului in caldura. Fortele disipative se opun miscarii, fiind orientate in sens opus vitezei. In timp, odata cu scaderea energiei sistemului scade treptat la zero si amplitudinea oscilatiilor iar miscarea inceteaza.
Un exemplu de forta disipativa suficient de des intalnit in practica si convenabil din punctul de vedere al calculului matematic il reprezinta forta de rezistenta pe care o intampina un corp la inaintarea sa printr-un fluid. Ea este proportionala cu viteza relativa a corpului fata de fluid si de sens invers cu aceasta adica:
![]() . (22)
. (22)
In acest caz ecuatia de miscare a sistemului este:
![]() (23)
(23)
Daca se noteaza ![]() si
si ![]() , atunci ecuatia de miscare
se scrie sub forma:
, atunci ecuatia de miscare
se scrie sub forma:
![]() (24)
(24)
unde s-a notat cu δ factorul de amortizare al oscilatiilor. Si ecuatia (24) este o ecuatie diferentiala de ordinul al doilea, liniara, omogena, cu coeficienti constanti, asa incat solutia ei se va gasi urmand aceeasi pasi ca si in rezolvarea ecuatiei (5).
Astfel, se cauta o solutie
de forma ![]() . Ecuatia caracteristica
a ecuatiei diferentiale (24) este:
. Ecuatia caracteristica
a ecuatiei diferentiale (24) este:
![]() (25)
(25)
Cazul 1. Daca discriminantul ecuatiei caracteristice
(25) este ![]() , atunci ecuatia admite
doua radacini reale, egale sau diferite intre ele dupa cum
se realizeaza egalitatea sau inegalitatea din conditia impusa.
Acestea sunt:
, atunci ecuatia admite
doua radacini reale, egale sau diferite intre ele dupa cum
se realizeaza egalitatea sau inegalitatea din conditia impusa.
Acestea sunt:
![]()
In cazul radacinilor reale si egale solutia ecuatiei diferentiale (24) se scrie sub forma :
![]() , (26)
, (26)
iar in cazul radacinilor reale si distincte sub forma:
![]() . (27)
. (27)
Atat intr-o situatie cat si in cealalta, din cauza frecarii foarte mari, miscarea efectuata de sistem nu este una oscilatorie. Sistemul nu va oscila de o parte si de alta a pozitiei sale de echilibru stabil, ci se va indrepta asimptotic catre aceasta pozitie. Acesta este cazul amortizarii critice. Din punct de vedere matematic aceasta se traduce prin faptul ca solutiile sunt functii exponentiale descrescatoare in timp.
|
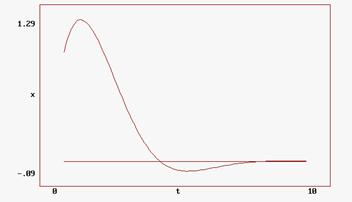
Fig. II.1
Cazul 2. Daca discriminantul ecuatiei
caracteristice (25) este ![]() , atunci radacinile ecuatiei caracteristice
sunt complex conjugate iar solutia generala va fi o combinatie
liniara de forma:
, atunci radacinile ecuatiei caracteristice
sunt complex conjugate iar solutia generala va fi o combinatie
liniara de forma:
![]() (28)
(28)
sau mai simplu:
![]() (29)
(29)
unde am folosit notatia ![]() . Ca si in cazul miscarii
oscilatorii armonice, constantele
. Ca si in cazul miscarii
oscilatorii armonice, constantele ![]() si
si ![]() sunt constante arbitrare de integrare, in
general complexe. Pentru ca elongatia miscarii oscilatorii amortizate
sa fie o marime reala ele trebuie sa verifice relatia
sunt constante arbitrare de integrare, in
general complexe. Pentru ca elongatia miscarii oscilatorii amortizate
sa fie o marime reala ele trebuie sa verifice relatia ![]() , unde cu asterisc s-a notat
conjugata complexa a constantei
, unde cu asterisc s-a notat
conjugata complexa a constantei ![]() . Utilizand din nou formula
lui Euler, se gaseste legea miscarii
oscilatorii amortizate:
. Utilizand din nou formula
lui Euler, se gaseste legea miscarii
oscilatorii amortizate:
![]() (30)
(30)
unde am notat cu
![]() (31)
(31)
si cu
![]() . (32)
. (32)
Se observa ca amplitudinea miscarii scade exponential in timp, tinzand asimptotic la zero,
![]() (33)
(33)
si ca perioada acesteia este constanta si nu depinde de valoarea amplitudinii:
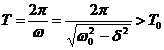 (34)
(34)
Asa cum se vede din (34), frecarea duce la cresterea perioadei oscilatorului amortizat fata de cea oscilatorului neamortizat. In figura de mai jos s-a reprezentat grafic relatia (30).
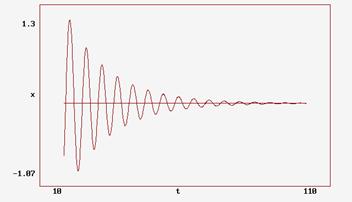
Fig. II.2
Decrementul logaritmic. Gradul de amortizare a miscarii se apreciaza cu ajutorul mai multor marimi. Una dintre ele este decrementului logaritmic al amplitudinii. Acesta se defineste ca fiind logaritmul natural al raportului oricaror doua amplitudini consecutive:
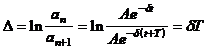 . (34)
. (34)
Se defineste de asemenea timpul de relaxare al amplitudinii, ![]() , ca fiind timpul dupa care amplitudinea miscarii
scade de e ori, unde e reprezinta baza logaritmului
natural. O alta marime specifica oscilatiilor amortizate
este factorul de atenuare,
, ca fiind timpul dupa care amplitudinea miscarii
scade de e ori, unde e reprezinta baza logaritmului
natural. O alta marime specifica oscilatiilor amortizate
este factorul de atenuare, ![]() . Pentru cazul
. Pentru cazul ![]() , miscarea este aperiodica iar pentru cazul
, miscarea este aperiodica iar pentru cazul ![]() , miscarea este periodica. In tabelul de mai jos sunt date ordinile de marime
pentru factorul de atenuare al catorva oscilatori amortizati:
, miscarea este periodica. In tabelul de mai jos sunt date ordinile de marime
pentru factorul de atenuare al catorva oscilatori amortizati:
Oscilatorul amortizat |
Factorul de atenuare Q |
|
Pamantul (miscari seismice) |
250-1400 |
|
Struna de vioara |
1000 |
|
Atomul excitat |
|
|
Nucleul excitat ( |
|
Tabelul II.1.
Pornind de la definitia timpului de relaxare, sa se defineasca timpul de injumatatire al amplitudinii, si sa se gaseasca o formula de calcul a acestuia.
Sa se gaseasca timpul de relaxare pentru energia totala a oscilatorului amortizat.
O masa m=150g suspendata la capatul unui resort de constanta elastica k=50N efectueaza oscilatii verticale amortizate. Stiind ca dupa n=15 oscilatii amplitudinea miscarii scade de e=2.71 ori sa se afle: a) decrementul logaritmic al miscarii; b) perioada oscilatiilor amortizate si constanta g
Un oscilator are m=0,01kg, k=0,49N/m, g=0,001N.s/cm Se stie in plus ca la momentul t=0, elongatia miscarii are valoarea x=0,02m iar viteza miscarii are valoare v=0.
a) Sa se gaseasca expresia elongatiei x in functie de timp; b) Care este timpul de relaxare pentru amplitudinea oscilatiilor? c) Care este valoarea factorului de calitate Q a oscilatorului?
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








