
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Transformata Laplace |
Transformata Laplace
Transformata Laplace
Fie
![]() astfel incat are sens
integrala improprie cu parametru
astfel incat are sens
integrala improprie cu parametru
![]() (1)
(1)
Definitie.
Daca are sens egalitatea (1), F se numeste transformata Laplace
a lui f si se noteaza si ![]() .
.
Functiile f pentru care exista transformata Laplace se numesc functii original (sau simplu, original), iar transformata Laplace F se mai numeste functia imagine (sau scurt imagine).
Definitie.
Functia f(x): ![]() (sau C), I interval marginit sau nemarginit, este derivabila
pe portiuni daca pentru orice interval compact
(sau C), I interval marginit sau nemarginit, este derivabila
pe portiuni daca pentru orice interval compact ![]() exista o
diviziune
exista o
diviziune ![]() cu
cu
![]()
astfel incat f(t) sa fie derivabila pe
fiecare interval ![]() si sa existe
limitele laterale
si sa existe
limitele laterale
![]() .
.
Definitie. Se numeste original o functie f(x), reala sau complexa, definita pe multimea numerelor reale si care satisface urmatoarele conditii:
1. f(x) = 0 daca x < ),
2. f(x) este derivabila pe portiuni,
3.
exista
numerele M > 0, ![]() astfel incat
astfel incat
![]() (2)
(2)
Numarul ![]() se numeste indicele
de crestere al functiei f(x).
se numeste indicele
de crestere al functiei f(x).
Multimea functiilor original se
noteaza cu ![]()
Proprietatile transformatei Laplace:
1.Este
liniara; pentru constantele ![]() si
si ![]() si originalele
si originalele ![]() si
si
![]() are loc egalitatea
are loc egalitatea
![]()
2.Pentru orice a>0 si f(x) original are loc egalitatea
![]() (3)
(3)
in care F(p) este imaginea functiei f(x).
Daca a > 0 si f(x) original atunci
![]() (4)
(4)
3.Daca
f(x) este original si ![]() o constanta
atunci
o constanta
atunci
![]() (5)
(5)
4.Teorema de derivare a originalului. Daca functia original f(x) este
de "n" ori derivabila, cu derivatele continue atunci
![]() (6)
(6)
5.Teorema
derivarii imaginii. Daca ![]() sunt
sunt
functii original atunci derivand egalitatea
![]()
in raport cu "p", obtinem formulele
![]() (7)
(7)
6.Teorema integrarii originalului. Daca f este original atunci
![]() (8)
(8)
7.Teoremele
de integrare a imaginii. Daca ![]() este original atunci
este original atunci
![]() (9)
(9)
Consecinte ale proprietatilor transformatei Laplace.
1. Daca
![]() si p >0 atunci
si p >0 atunci
![]() (10)
(10)
|
In
particular, pentru ![]() obtinem
obtinem ![]()
Pentru ![]() obtinem
obtinem
![]() (11)
(11)
2. Utilizand teoreme integrarii imaginii rezulta
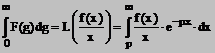 (12)
(12)
si pentru p = 0 obtinem
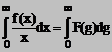 (13)
(13)
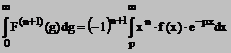 (14)
(14)
care pentru p = 0 devine
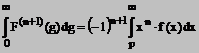 (15)
(15)
Pentru n = 0, egalitatea (15) devine
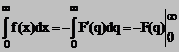 (16)
(16)
Aplicatii.
1.Sa se arate ca
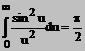
Rezolvare Fie functia
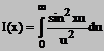
careia sa-i calculam transformata Laplace.
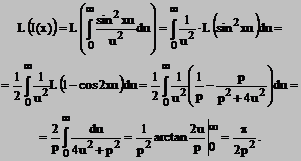
Deci
![]() si
si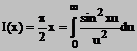
Trecand
la limita pentru ![]() obtinem
obtinem
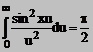 .
.
2.Integrati ecuatia diferentiala, liniara, cu coeficienti constanti si neomogena
![]()
cu
conditiile initiale ![]()
Rezolvare. Teorema derivarii originalului conduce la
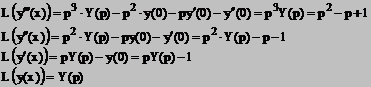
si ![]()
Se obtine ecuatia operationala
![]()
din care
![]()
Functia original corespunzatoare, solutie a ecuatiei, are forma
![]()
3. Integrati ecuatia diferentiala, liniara, cu coeficienti constanti si neomogena
![]()
si
![]()
Rezolvare. Ecuatia se mai poate scrie
![]()
Ecuatia
operationala are forma ![]() , din care
, din care
![]()
Utilizand teorema derivarii imaginii se obtine
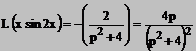
iar
![]()
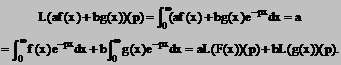
1. Proprietatile de omotetie
![]()
![]()
(1) si (2) pot fi exprimate mai simplu astfel
![]()
![]()
Demonstratie:
![]()
![]()
![]()
2. Prima teorema de
translatie foloseste functia unitate a lui Heaviside H(x)=0 pentru x < 0 si H(x) = 1
pentru ![]()
2.1. Prima teorema de translatie
![]() (1)
(1)
Intr-adevar,
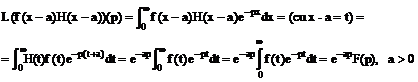
Daca relatia (3) se
foloseste de la dreapta la stanga, trebuie tinut cont ca originalul
H(x-a)=0 pentru x < a si atunci, fara a mai utiliza
functia unitate avem:![]()
2.2. A doua teorema de translatie
![]() (2)
(2)
Intr-adevar,
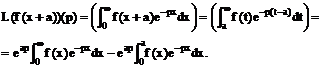
3. Teorema de deplasare
![]() (3)
(3)
![]()
Din proprietatea a doua de omotetie si din teorema de deplasare, deci din (2) si (5), obtinem
![]() (4)
(4)
4. Teorema de derivare a originalului
![]() (5)
(5)
valabila daca ![]() si are sens
si are sens ![]()
Demonstratie
![]()
Deci f(x)=p F(p)-f(0+) si pentru n=1, (7) se verifica. Pentru n = 2 avem:
![]() (tinand cont de rezultatul pentru n = 1 obtinem) =
(tinand cont de rezultatul pentru n = 1 obtinem) = ![]() Pentru n>2
iteram acest procedeu.
Pentru n>2
iteram acest procedeu.
Operatia de derivare in spatiul functiilor original se transforma in operatia de inmultire cu p in spatiul functiilor imagine, abstractie facandu-se de un polinom in p.
5. Teorema derivarii imaginii
In ipoteza
ca ![]() sunt functii
original se poate argumenta posibilitatea derivarii sub integrala in
raport cu p in relatia de definitie
sunt functii
original se poate argumenta posibilitatea derivarii sub integrala in
raport cu p in relatia de definitie
![]()
Obtinem formulele
![]() ) (8)
) (8)
Deci si acestei operatii de derivare ii corespunde operatia de inmultire cu "x".
6. Teorema integrarii originalului
![]() (9)
(9)
Demonstratie Fie ![]() . Cum
. Cum ![]() si g(0+) = 0 (din modul de definire a lui g).
si g(0+) = 0 (din modul de definire a lui g).![]()
Deci ![]() de unde (9) are loc.
de unde (9) are loc.
7. Teorema de integrare a imaginii este data prin relatia
![]() (10)
(10)
valabila
cand ![]() este functie
original.
este functie
original.
Demonstratie
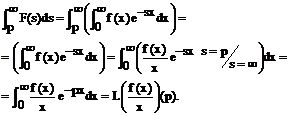
Din faptul ca
![]()
si din teorema de deplasare: ![]() obtinem
ca
obtinem
ca
![]()
Se poate arata cu ajutorul teoremei de convolutie ca
![]() (11)
(11)
Cu ajutorul teoremei de integrare a imaginii
![]()
putem calcula integrale de forma
![]()
cu formula
![]()
Intr-adevar,
![]()
se mai scrie
![]()
Facand p = 0 obtinem relatia cautata.
a) ![]() atunci cu d avem
atunci cu d avem
![]()
b) pentru a > 0, b > 0
![]()
Intr-adevar, avem
![]()
c) Integralele lui Froullani
1. ![]()
2. ![]()
3. ![]()
Cu teorema de deplasare si faptul ca
![]() obtinem ca:
obtinem ca: ![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








