
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Procesul de esantionare |
Procesul de esantionare
Procesul de esantionare
1.1 Procesul de esantionare ideala
Fie f(t) o functie de timp ce este esantionata cu un esantionator ideal. Fie T perioada de esantionare. Iesirea esantionatorului ideal, f*(t), este un tren de impulsuri cu amplitudinea egala cu cea a semnalului de intrare la momentele de esantionare. Notam cu
![]()
un tren de impulsuri unitare, unde
![]()
Esantionatorul ideal este un contact care se inchide la fiecare T secunde pentru o durata de timp 0. Iesirea esantionatorului ideal este
![]()
unde esantionarea a
inceput la momentul t = 0. Transformata Laplace a functiei ![]() este 1, iar
Tansformata Laplace a functiei
este 1, iar
Tansformata Laplace a functiei ![]() este e-kTs.
Transformata Laplace a functiei f*(t) este
este e-kTs.
Transformata Laplace a functiei f*(t) este
![]()
Semanlele de intrare, trenul de impulsuri unitare si de iesire ale esantionatorului ideal sunt cele din Figura 11, Figura 12 si Figura 13.
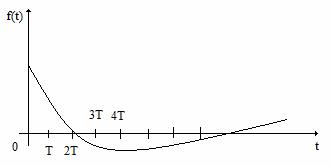
Figura 11 . Semnalul de intrare in esantionatorul ideal.
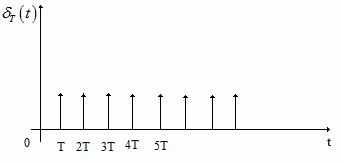
Figura 12 . Trenul de impulsuri unitare.
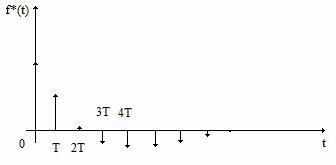
Figura 13 . Semnalul de iesire al esantionatorului ideal.
Fie F(s) transformata
Laplace a functiei f(t) si P(s) transformata Laplace a functiei ![]() .
.
![]()
pentru ![]() .
.
Deoarece f*(t) este produsul a doua functii de timp
![]()
transformata Laplace a functiei f*(t) se poate calcula ca
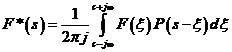
unde c este abscisa de
convergenta a integralei. Integrala se poate calcula cu teorema
reziduurilor. Pentru aceasta trebuie sa calculam polii
functiilor ![]() si
si ![]() .
.
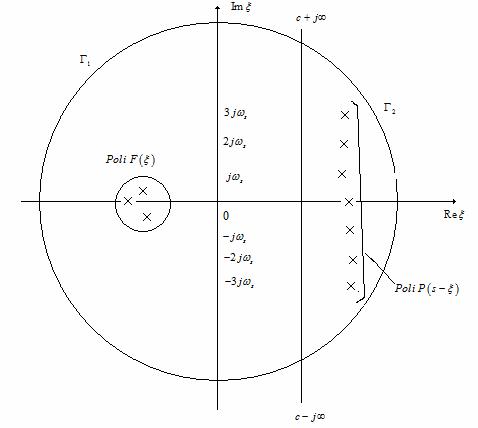
Figura 14 . Integralele de contur pentru calculul functiei F*(s).
Polii functiei ![]() sunt situati in
semiplanul stang. Polii functiei
sunt situati in
semiplanul stang. Polii functiei ![]() sunt simplii, in
numar infinit, si au valorile
sunt simplii, in
numar infinit, si au valorile
![]() ,
, ![]()
unde T este perioada de
esantionare, iar ![]() este pulsatia de
esantionare in rad/s. Distributiile tipice ale acestor poli sunt cele
din Figura 14.
este pulsatia de
esantionare in rad/s. Distributiile tipice ale acestor poli sunt cele
din Figura 14.
Vom calcula integrala
separat pe contururile ![]() si
si ![]() . Daca
. Daca
![]()
atunci integralele pe
semicercurile cu raze infinite din contururile ![]() si
si ![]() sunt nule. Integrala
pe conturul
sunt nule. Integrala
pe conturul ![]() se calculeaza
astfel.
se calculeaza
astfel.
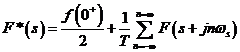
Termenul ![]() are urmatoarea
explicatie. Daca functia f(t) este discontinua,
transformata Laplace inversa are ca rezultat in punctele de
discontinuitate media valorilor laterale ale functiei in acele puncte. In
definitia functiei f*(t), daca functia f(t) este
discontinua in punctele de esantionare, functia f*(t) are ca valoare
limita din dreapta a functiei f(t) ce se esantioneaza. In
formula s-a pus in evidenta termenul
are urmatoarea
explicatie. Daca functia f(t) este discontinua,
transformata Laplace inversa are ca rezultat in punctele de
discontinuitate media valorilor laterale ale functiei in acele puncte. In
definitia functiei f*(t), daca functia f(t) este
discontinua in punctele de esantionare, functia f*(t) are ca valoare
limita din dreapta a functiei f(t) ce se esantioneaza. In
formula s-a pus in evidenta termenul ![]() deoarece sunt cazuri
cand functia f(t) este discontinua in origine.
deoarece sunt cazuri
cand functia f(t) este discontinua in origine.
Integrala pe conturul ![]() se calculeaza
astfel. Fie
se calculeaza
astfel. Fie
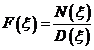
Presupunem pentru simplitate ca polii functiei sunt simpli. Fie
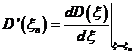
unde ![]() este un pol al
functiei
este un pol al
functiei ![]() , n = 1, 2, ., k.
, n = 1, 2, ., k.
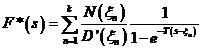
Exemple. Fie functia treapta unitara f(t) = 1(t) esantionata la intervale egale cu T. Iesirea esantionatorului ideal este
![]()
Transformata Laplace a functiei, F*(s) este
![]() , pentru
, pentru ![]()
Sa calculam
F*(s) pe conturul ![]() .
. ![]() deci N(s) = 1, D'(s) =
1, deci
deci N(s) = 1, D'(s) =
1, deci
![]()
1.2 Teorema esantionarii
Fie functia de
intrare f(t) ce este esantionata cu perioada T. Presupunem ca
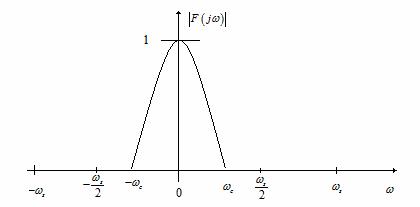
cea mai mare pulsatie continuta in f(t) este ![]() . Spectrul functiei de intrare f(t) este cel din Figura 15.
. Spectrul functiei de intrare f(t) este cel din Figura 15.
|
Figura 15 . Spectrul functiei de intare f(t).
Spectrul functiei esantionate f*(t) este cel din Figura 16.
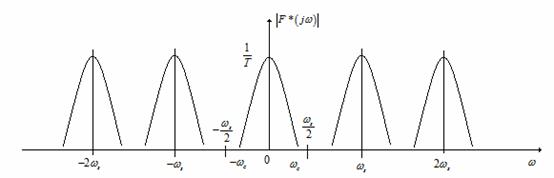
Figura 16 . Spectrul functiei esantionate f*(t).
Esantionatorul ideal
reproduce la iesire spectrul semnalului continuu de la intrare si
componentele sale repetate la multiplii pulsatiei de esantionare.
Componentele au amplitudinea 1/T. Dupa cum se vede din Figura 16, daca pulsatia de esantionare ![]() , semnalul continuu f(t) poate fi refacut din cel
esantionat f*(t) cu ajutorul unui filtru trece-jos. Teorema
esantionarii spune ca un semnal continuu ce nu contine
pulsatii mai mari ca
, semnalul continuu f(t) poate fi refacut din cel
esantionat f*(t) cu ajutorul unui filtru trece-jos. Teorema
esantionarii spune ca un semnal continuu ce nu contine
pulsatii mai mari ca ![]() rad/s, este complet
caracterizat de valorile semnalului masurate la instante de timp
separate de
rad/s, este complet
caracterizat de valorile semnalului masurate la instante de timp
separate de ![]() secunde.
secunde.
1.3 Refacerea semnalelor esantionate
In general, componentele sistemelor de conducere sunt actionate de semnale continue. In consecinta, intre componentele numerice si cele anologice se introduce un dispozitiv de refacere a datelor. Cel mai obisnuit circuit de refacere a semnalelor analogice este dispozitivul de retinere.
Fie un dispozitiv de
esantionare ideal care esantioneaza cu o pulsatie ![]() , a carui caracteristica spectru
frecventa este cea din Figura
17. Din figura se vede ca semnalul terbuie
filtrate cu un filtru trece-jos ideal ca cel din Figura 18.
, a carui caracteristica spectru
frecventa este cea din Figura
17. Din figura se vede ca semnalul terbuie
filtrate cu un filtru trece-jos ideal ca cel din Figura 18.
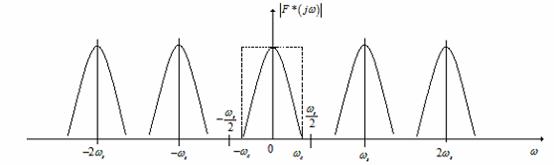
Figura 17 . Refacerea semnalelor analogice cu un filtru trece-jos.
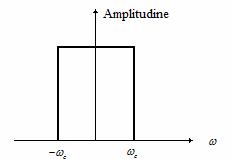
Figura 18 . Caracteristica amplitudine a unui filtru ideal.
Un filtru trece-jos ideal nu este fizic realizabil. Chiar daca s-ar putea realize un asemenea filtru, presupunerea ca semnalul continuu este de banda limitata nu este totdeauna indeplinita. Pentru aplicatiile practice este deci imposibila o refacere a semnalului continuu dupa ce a fost esantionat. Refacerea semnalului esantionat se face prin aproximarea functiei de timp originale.
La refacerea semnalului avem esantioanele f(0), f(T), ., f(kT). O metoda ce se poate utilize pentru refacerea valorilor semnalului intre momentele de esantionare, kT si (k+1)T este aceea a dezvoltarii in serie. Fie
fk(t) = f(t) pentru kT <= t < (k+1)T
![]()
Pentru a evalua derivate din formula de mai sus avem disponibile doar valorile functiei f(t) in momentele de esantionare. Este posibil sa estimam derivatele prin diferente finite, de exemplu derivate de ordin intai
![]()
Deoarece aproximarea derivatelor de ordin superior duce la circuite complexe, de obicei se utilizeaza aproximarea
fk(t) = f(t) pentru kT <= t < (k+1)T
care se numeste extrapolator de ordin zero. El mentine valoarea esantionata pe timpul perioadei de esantionare, pana la urmatorul esantion. Pentru a deduce functia de transfer a extrapolatorului de ordin zero vom considera raspunsul sau la impuls din
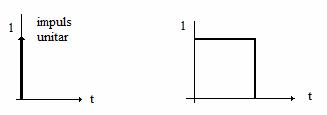
Figura 19. Impuls unitar si raspunsul la impuls unitar al extrapolatorului de ordin zero.
Notam cu 1(t) functia treapta unitara, si raspunsul la impuls al extrapolatorului este
y(t) = 1(t) - 1(t-T)
Functia de transfer a extrapolatorului de ordin zero va fi
![]()
Intrarea intr-un element de extrapolare este cea din Figura 20.
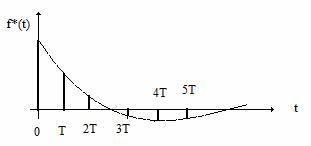
Figura 20 . Semnalul de intrare in extrapolator.
Iesirea extrapolatorului este cea din Figura 21.
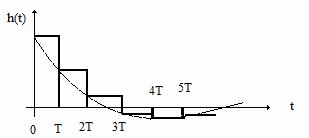
Figura 21 . Iesirea extrapolatorului.
Pentru a determina
caracteristicile de amplitudine si faza ale ale extrapolatorului, vom
inlocui in functia sa de transfer H0(s) pe s cu ![]() si obtinem
si obtinem
![]()
care se poate rescrie
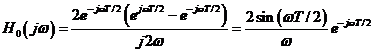
sau
![]()
Deoarece perioada de esantionare T este
![]()
putem scrie
![]()
Caracteristica amplitudine a extrapolatorului este cea din Figura 22, iar cea de faza din Figura 23.
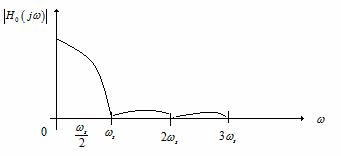
Figura 22 . Caracteristica amplitudine a extrapolatorului de ordin zero
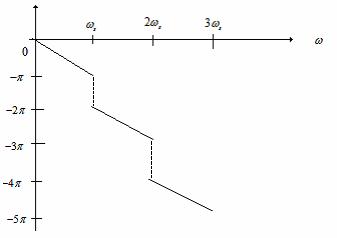
Figura 23 . Caracteristica de faza a extrapolatorului de ordin zero.
1.4 Transformata Z
Pentru analiza si proiectarea sistemelor de reglare discrete se utilizeaza transformata Z. Ea are un rol similar celui al transformatei Laplace pentru sistemele continue.
Fie f(t) o functie de timp ce este esantionata cu un esantionator ideal. Fie T perioada de esantionare. Iesirea esantionatorului ideal, f*(t), este un tren de impulsuri cu amplitudinea egala cu cea a semnalului de intrare la momentele de esantionare. Transformata Laplace a functiei f*(t) este
![]()
Functia F*(s) nu este
rationala din cauza factorului ![]() si este dificil
de a calcula transformata Laplace inversa. Functia F*(s) se poate
transforma intr-o functie rationala cu transformarea
si este dificil
de a calcula transformata Laplace inversa. Functia F*(s) se poate
transforma intr-o functie rationala cu transformarea
![]()
Din aceasta relatie deducem
![]()
Reamintim ca T este perioada de esantionare, iar z este o variabila complexa pentru care
![]()
![]()
cu ![]()
Transformata Z a functiei f(t), notata F(z) se defineste ca
![]()
O metoda de calcul a
transformatei Z este aceea de a face substitutia ![]() in expresia
functiei F*(s).
in expresia
functiei F*(s).
O alta metoda este urmatoarea. Fie
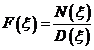
Presupunem pentru simplitate ca polii functiei sunt simpli. Fie
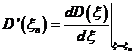
unde ![]() este un pol al
functiei
este un pol al
functiei ![]() , n = 1, 2, ., k. Am aratat ca
, n = 1, 2, ., k. Am aratat ca
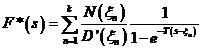
Atunci transformata Z are expresia
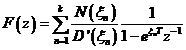
Deoarece transformata Z a functiei f(t) se obtine din transformata Laplace a functiei f*(t), vom considera ca orice functie care are o transformata Laplace are si transformata Z.
Exemplu. Fie functia treapta unitara f(t) = 1(t) esantionata la intervale egale cu T. Dupa cm am aratat, transformata Laplace a functiei esantionate f*(t) este
![]()
si este
convergenta pentru ![]()
![]()
Cu substitutia ![]() obtinem
obtinem
![]()
pentru ![]() sau |z| > 1.
Acelasi rezultat se obtine cu a doua metoda. Deoarece
transformata Laplace a functiei 1(t) este 1/s, care are un pol simplu la s
= 0. Avem
N(s) = 1, D(s) = s si D'(s) = 1. Transformata Z a functiei va fi
sau |z| > 1.
Acelasi rezultat se obtine cu a doua metoda. Deoarece
transformata Laplace a functiei 1(t) este 1/s, care are un pol simplu la s
= 0. Avem
N(s) = 1, D(s) = s si D'(s) = 1. Transformata Z a functiei va fi
![]()
Exemplu. Fie functia ![]() unde a este o
constanta reala. Transformata Z a acestei functii este
unde a este o
constanta reala. Transformata Z a acestei functii este
![]()
Aceasta serie este convergenta pentru
![]()
de unde obtinem
![]()
Cu a doua metoda se procedeaza astfel. Transformata Laplace a functiei f(t) este
![]()
care are un pol simplu la s = -a. Avem N(s) = 1, D(s) = s + a si D'(s) = 1. Transformata Z functiei va fi
![]()
1.5 Teoremele transformatei Z
daca ![]() si f
si f![]() au transformatele Z
au transformatele Z ![]() si
si ![]() , atunci:
, atunci:
![]()
![]()
unde a este o constanta.
daca ![]() are transformata Z
are transformata Z ![]() , atunci
, atunci
![]()
daca ![]() are transformata Z
are transformata Z ![]() , atunci
, atunci
![]()
daca ![]() are transformata Z
are transformata Z ![]() , si daca limita
, si daca limita ![]() exista, atunci
exista, atunci
![]()
daca ![]() are transformata Z
are transformata Z ![]() , si daca
functia
, si daca
functia ![]() nu are poli pe cercul
unitar sau in afara lui, atunci
nu are poli pe cercul
unitar sau in afara lui, atunci
![]()
daca ![]() si f
si f![]() au transformatele Z
au transformatele Z ![]() si
si ![]() si
si ![]() pentru t < 0, atunci
pentru t < 0, atunci
![]()
1.6 Functiile de transfer ale sistemelor discrete
Fie sistemul continuu din Figura 27 cu intrarea u(t) si iesirea y(t).
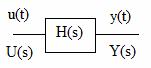
Figura 27 . Sistem liniar cu intrare continua.
Sistemul este descris de functia de transfer
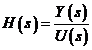
Fie acelasi sistem cu intrarea o functie esntionata u*(t) din Figura 28
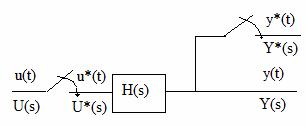
Figura 28 . Sistem liniar cu intrare esantionata.
Iesirea Y(s) a sistemului din Figura 28 este
![]()
Vrem sa calculam transformata Z a iesirii sistemului, Y(z). Pentru aceasta consideram un esantionator fictive la iesire si procedam astfel
![]()
Utilizam proprietatea de periodicitate a functiei U*(s) si obtinem
![]()
Definim functia de transfer esantionata
![]()
si avem
![]()
sau, cu transformarea, ![]()
Y(z) = H(z) U(z)
Fie acum doua elemente continue cu functiile de transfer H1(s) si H2(s), conectate in serie separate de un element de esantionare, ca in Figura 29.
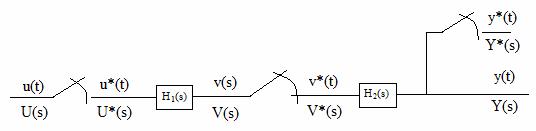
Figura 29 . Elemente in serie separate de un element de esantionare.
Avem in acest caz
![]()
si
![]()
de unde se deduce
![]()
In cazul cand sistemul contine elemente conectate in serie, neseparate de un element de esantionare, ca in Figura 30 avem
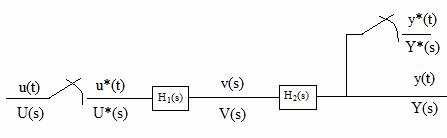
Figura 30 . Sistem cu elemente serie.
![]()
unde s-a notat
![]()
1.7 Functia de transfer a exptrapolatorului de ordin zero
Functia de transfer a extrapolatorului de ordin zero este
![]()
Transformata Z a acestei functii de transfer este
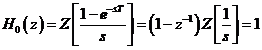
In general, extrapolatorul de ordin zero este urmat de un bloc continuu, ca in Figura 31.

Figura 31 . Sistem cu esantionator.
In acest caz, transformata Z a iesirii va fi
![]()
Functia de transfer corespunzatoare va fi
![]()
Exemplu. Fie functia de transfer H(s) a sistemului din Figura 31
![]()
Functia de transfer G(z) va fi
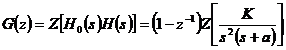
1.8 Chestiuni de studiat
1. Sa se determine tansformata Laplace si transformata Z a functiei treapta unitara esantionata cu perioada T.
2. Sa se determine tansformata Laplace si transformata Z a functiei f(t) = sin ωt esantionata cu perioada T.
3. Sa se determine tansformata Laplace si transformata Z a functiei f(t) = e-at esantionata cu perioada T, unde a > 0 este o constanta.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Referate pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








