
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica Aliaje. diagrame de echilibru |
Aliaje. diagrame de echilibru
ALIAJE. DIAGRAME DE ECHILIBRU
1. CONSTITUTIA ALIAJELOR
Prin sistem fizico-chimic se intelege un corp sau un ansamblu de corpuri care se gasesc in interactiune si care se izoleaza de mediul inconjurator, ca de exemplu topitura metalica dintr-un creuzet, o bucata de metal sau aliaj etc. Sistemele fizico-chimice pot fi omogene daca au aceleasi caracteristici fizico-chimice in toata masa lor, sau eterogene, daca sunt formate din mai multe parti omogene fizic si chimic. O parte omogena a unui sistem eterogen se numeste faza.
Materialele metalice se impart in metale si aliaje. In cazul metalelor, existand o singura specie de atomi, la solidificare se va forma o singura faza, respectiv metal pur.
Aliajele sunt materiale metalice obtinute prin amestecul intim, uneori la scara atomica, a unui metal de baza cu alte elemente metalice sau nemetalice, aceste amestecuri realizandu-se de cele mai multe ori prin topire si solidificare.
Totalitatea aliajelor alcatuite din aceiasi componenti, formeaza un sistem de aliaje. De exemplu: totalitatea aliajelor formate din cupru si nichel, care contin cupru de la 0 - 100 % - restul nichel, formeaza sistemul de aliaje cupru-nichel. Dupa numarul componentilor (speciilor atomice din aliaj), aliajele pot fi binare, ternare, cuaternare sau polinare, respectiv pe langa componentul de baza mai sunt prezenti unul, doi, trei sau mai multi alti componenti, numiti si componenti de aliere sau elemente de aliere. Componentul de baza este intotdeauna metalic, iar elementele de aliere pot fi, fie metalice fie nemetalice.
In ansamblu, un aliaj este omogen Ia scara macroscopica, dar privit la scara microscopica el este format din numerosi graunti cristalini, care daca sunt de aceiasi natura, aliajul este monofazic, iar daca grauntii sunt de natura diferita, aliajul este polifazic. Aliajele polifazice, desi apar omogene macroscopic, sunt eterogene la scara microscopica, fiind alcatuite din domenii de faze diferite. Proprietatile aliajelor sunt influentate de natura, cantitatea, forma si distributia fazelor.
Natura fazelor prezente intr-un aliaj reprezinta constitutia fizico-chimica a aliajului. Asa cum s-a aratat, faza este definita ca o parte omogena dintr-un sistem fizico-chimic, delimitata de alte faze din sistem, prin suprafete de separare interfazica.
Din punct de vedere al constitutiei fizico-chimice, componentii unui aliaj se pot asocia in urmatoarele moduri:
- formeaza o combinatie sau un compus chimic;
- formeaza cristale separate de metal pur;
- atomii elementelor de aliere se incorporeaza in reteaua cristalina a metalului de baza formand cristale de solutie solida. Exista deci trei tipuri de faze in aliajele solide: metal pur, solutie solida, compus chimic.
In conditii de echilibru termodinamic, echilibru care in aliaje se realizeaza prin solidificare lenta sau prin incalziri in stare solida urmate de racire lenta (recoaceri), constitutia fizico-chimica pe care o adopta aliajul (numarul, natura, proportia fazelor) corespunde energiei libere minime.
La un aliaj binar, in care atomii celor doi componenti sunt notati cu A si B, apar in stare topita doua posibilitati:
- atomii celor doi componenti se separa dupa densitatile lor, respectiv componentii A si B sunt insolubili in stare lichida;
- atomii componentilor A si B se dizolva unul intr-altul formand o topitura omogena numita solutie lichida, in care atomii isi pierd individualitatea, distribuindu-se dezordonat.
La solidificarea aliajelor cu componenti insolubili in stare lichida vor rezulta doua faze solide, adica metal pur A si metal pur B.
In cazul solidificarii aliajelor a caror componenti sunt solubili in stare lichida apar trei posibilitati:
a) Atomii A si B se resping ceea ce inseamna ca fortele de atractie dintre atomii de acelasi fel sunt mai mari decat cele dintre atomii diferiti, deci atomii fiecarui component se grupeaza, rezultand un amestec de faze solide (metal pur A si metal pur B). De exemplu, in aceasta categorie se incadreaza aliajele din sistemul Pb-Sb; desi atomii de plumb si cei de stibiu formeaza un lichid omogen, la solidificare se vor forma domenii alcatuite numai din atomi de plumb si altele numai din atomi de stibiu.
b) Atomii A si B sunt indiferenti, ceea ce inseamna ca fortele de atractie dintre atomii de acelasi fel sunt de acelasi ordin de marime cu fortele de atractie dintre atomii diferiti. In acest caz atomii componentilor A si B se vor repartiza la intamplare formand o faza unica, respectiv o solutie solida.
c) Atomii A si B se atrag, ceea ce inseamna ca fortele de atractie dintre atomii de acelasi fel sunt mai mici decat cele dintre atomii diferiti. In acest caz fiecare atom A se va inconjura de un anumit numar de atomi B formand in acel domeniu o faza unica, respectiv un compus chimic. Caracteristic pentru compusii chimici este faptul ca poseda o structura cristalina deosebita de cea a elementelor constituente.
2. CONSTITUENTI METALOGRAFICI
La examinarea microscopica, fazele dintr-un material metalic prezinta aspecte structurale caracteristice, numite constituenti structurali sau metalografici.
Proprietatile aliajelor sunt determinate de tipul fazelor prezente in aliaj, dar si de modul in care sunt distribuiti constituentii metalografici, de forma si de raportul lor cantitativ. Deci, in timpul cercetarii microscopice, prin studierea tipului, formei, cantitatii si distributiei constituentilor metalografici, se vor putea face aprecieri asupra proprietatilor metalelor sau aliajelor.
Constituentii metalografici pot fi grupati in patru categorii distincte:
- metalul pur;
- solutia solida;
- compusul chimic;
- amestecul mecanic.
2.1. Metalul pur
In cazul examinarii microscopice a unui esantion de metal pur, daca atacul suprafetei supuse cercetarii a fost de scurta durata, vor fi atacate doar limitele cristalelor, evidentiindu-se deci graunti de metal pur. In cazul in care atacul suprafetei de cercetat a fost de mai lunga durata, grauntii vor fi atasati in mod diferit, respectiv se vor colora diferit. Acest lucru este datorat anizotropiei grauntilor si orientarii diferite de la graunte la graunte a retelei cristaline.
Metalul pur se caracterizeaza prin conductibilitate electrica si termica ridicata, plasticitate mare, dar cu duritate, limita de curgere si rezistenta la rupere, scazute.
In cadrul aliajelor, atunci cand componentii aliajului sunt insolubili in stare solida, ei pot sa apara ca domenii distincte, respectiv graunti separati de metal pur.
2.2. Solutia solida
Grauntii de solutie solida sunt formati din atomi ai unor componenti diferiti care sunt distribuiti intamplator in cadrul retelei. Componentul care predomina este numit component de baza sau solvent, iar in reteaua sa cristalina vor fi inglobati atomii componentului de aliere, respectiv componentului dizolvat.
Dupa modul in care se incadreaza atomii componentilor dizolvati in reteaua cristalina a solventului, vor rezulta solutii solide de substitutie, de interstitie si complexe. In solutiile solide de substitutie, atomii componentului de aliere inlocuiesc in nodurile retelei cristaline o parte din atomii metalului de baza. In solutiile solide de interstitie atomii componentului de aliere ocupa pozitii interstitiale ale retelei metalului de baza. In solutiile solide complexe apar atomi straini, atat in nodurile retelei, cat si in spatiile interstitiale.
In figurile 1, 2 si sunt prezentate schematic principalele tipuri de solutii solide, respectiv solutiile de substitutie, solutiile solide de interstitie si solutiile solide complexe.
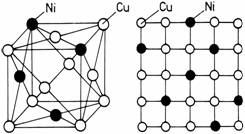
Figura 1. Solutie solida de substitutie in sistemul Cu-Ni: a) reprezentare in spatiu; b) reprezentare in plan.
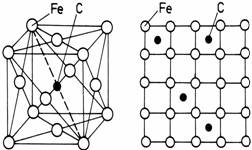
Figura 2. Solutie solida de interstitie de carbon in Fegama: a) reprezentare in spatiu; b) reprezentare in plan.
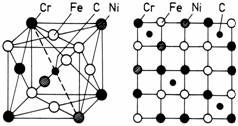
Figura Solutie solida complexa in aliajul polinar Fe-Cr-Ni-C: a) reprezentare in spatiu; b) reprezentare in plan.
Daca metalele care formeaza solutii solide sunt complet solubile in stare solida, toti atomii componentului de baza pot fi substituiti prin atomi ai componentului de aliere si se pot forma astfel, solutii solide la orice concentratie a elementului de aliere (de la 0 - 100 %).
Pentru a se putea forma solutii solide cu solubilitate nelimitata (solutii solide totale), componentii aliajului trebuie sa indeplineasca urmatoarele conditii:
a) sa aiba acelasi tip de retea cristalina;
b) diferenta dintre diametrele atomilor sa nu fie mai mare de 8 %;
c) sa ocupe pozitii apropiate in tabelul periodic al elementelor, adica sa aiba un caracter electrochimic asemanator;
d) sa aiba temperaturi de topire apropiate.
Daca componentii aliajului nu indeplinesc toate conditiile enumerate mai sus, se vor putea forma doar solutii solide partiale. Daca diferenta dintre diametrele atomilor componentilor variaza in limitele 8 - 15 %, atunci solubilitatea este limitata, iar solutii solide de substitutie se vor putea forma numai in anumite intervale de concentratie. Daca diferenta dintre diametrele atomilor componentilor este mai mare de 15 %, intre componenti nu se vor putea forma solutii solide de substitutie.
Solutiile solide de interstitie se formeaza prin dizolvarea intr-un solvent metalic, a unor elemente cu diametrul atomic foarte mic (hidrogen cu d = 0,92 Z, azot cu d = 1,42 Z, carbon cu d = 1,54 Z, bor cu d = 1,94 Z). Ca solvent pentru solutiile solide de interstitie servesc de regula metalele de tranzitie (Fe, Mn, Cr) la care factorul electrochimic este favorabil. Solutiile solide interstitiale cu cea mai mare importanta tehnica, apar in aliajele fier-carbon.
Dimensiunile atomilor de C, H, B sunt mai mari decat cele ale spatiilor interstitiale ale retelei solventului metalic. Din aceasta cauza, dizolvarea introduce deformari elastice considerabile in reteaua solventului, ceea ce limiteaza solubilitatea la valori reduse, asa incat numai o proportie redusa din totalitatea interstitiilor vor putea fi ocupate. Datorita deformarii retelei si a tensiunilor interne ce apar, proprietatile mecanice ale solutiilor solide de interstitie sunt diferite de cele ale metalului de baza, chiar daca concentratia elementelor dizolvate interstitial este scazuta.
Solutiile solide complexe sunt combinatii intre solutiile solide de substitutie si cele de interstitie, respectiv in reteaua cristalina a metalului de baza apar atat atomi de substitutie cat si atomi interstitiali.
In solutiile solide legatura interatomica este de tip metalic, adica atomii tuturor componentilor (solvent si elemente dizolvate, fie ele metalice sau nemetalice) sunt ionizati pozitiv si sunt legati impreuna prin atractia exercitata de multimea electronilor de valenta colectivizati, care circula cvasi-liber prin scheletul ionic al retelei.
Introducerea atomilor straini, produce distorsionarea retelei cristaline a metalului de baza si deci proprietatile solutiei solide vor fi influentate de distributia acestor atomi straini din retea. In figura 4 sunt prezentate cateva situatii de deformare a retelei datorate prezentei atomilor straini cu diametre atomice diferite de cele ale metalului de baza. Se observa ca in prezenta atomilor elementelor de aliere apar in retea defecte punctiforme, precum si dislocatii. Cu cat continutul in elemente de aliere va fi mai mare cu atat numarul de defecte pe unitatea de volum va fi si el mai ridicat si deci duritatea si rezistenta la rupere vor fi mai mari, iar alungirea la rupere mai mica. In figura 5 este prezentata variatia rezistentei la rupere si a alungirii la rupere in functie de compozitia chimica, in cazul sistemului cu solutie solida totala Cu-Ni.
Comparand proprietatile mecanice ale solutiilor solide cu cele ale celorlalti constituenti, se poate face afirmatia ca aceste proprietati sunt mai apropiate de cele ale metalelor pure, adica duritatile si rezistentele Ia rupere sunt relativ scazute, iar alungirea la rupere este ridicata.
|
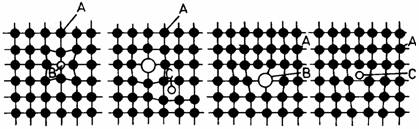
Figura 4. Distorsiuni in reteaua cristalina a solutiilor solide.
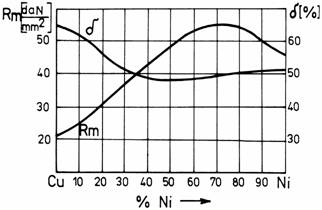
Figura 5. Variatia rezistentei la rupere si a alungirii la rupere in sistemul Cu-Ni
2. Compusul chimic
In conditiile in care intre atomii metalului de baza si atomii elementelor de aliere se stabilesc legaturi chimice, iau nastere asa numitii compusi chimici. Compusul chimic este un constituent metalografic care prezinta o compozitie chimica constanta si bine definita, iar reteaua sa cristalina este diferita de cea a componentilor.
Datorita legaturilor chimice complexe care apar intre atomii componentilor aliajelor, compusii chimici prezinta de regula o duritate ridicata, dar si o fragilitate mare. De asemeni compusii chimici prezinta de obicei temperaturi de topire mai mari decat elementele componente. Astfel, prezenta in aliaje a compusilor chimici, va determina cresterea duritatii si deci si a rezistentei la uzare, cresterea fragilitatii si ridicarea temperaturii de topire.
Se pot deosebi trei tipuri de compusi chimici: compusi electrochimici, compusi chimici electronici si compusi chimici interstitiali.
2.4. Amestecul mecanic
Amestecul mecanic este un constituent format din doua sau mai multe faze solide, care s-au separat fie dintr-o solutie lichida (amestec mecanic eutectic), fie dintr-o solutie solida suprasaturata (amestec mecanic eutectoid).
In diverse aliaje se formeaza amestecuri mecanice intre un metal pur si o solutie solida, sau intre un metal pur si un compus chimic, sau intre un compus chimic si o solutie solida etc. Fazele constituente ale amestecurilor mecanice se pot prezenta ca lamele sau globule ale unei faze, in masa celeilalte faze. Amestecurile mecanice eutectoide prezinta o dispersie mai ridicata a fazelor, ele sunt deci mai fine decat amestecurile mecanice eutectice.
Proprietatile amestecurilor mecanice sunt determinate de proprietatile fazelor constituente, respectiv proprietatile sunt intermediare. De asemeni proprietatile amestecurilor mecanice sunt influentate si de dispersia fazelor, cu cat aceasta este mai avansata cu atat rezistenta Ia rupere este mai mare.
DIAGRAMELE DE ECHILIBRU ALE ALIAJELOR BINARE
Proprietatile unui aliaj sunt determinate de constitutia sa fizico-chimica si nu in mod direct de compozitia chimica. Limitele de stabilitate ale fazelor dintr-un sistem de aliaje sunt reprezentate grafic in functie de temperatura si concentratie, rezultand asa numitele diagrame de echilibru fazic ale sistemelor. Pe aceste diagrame pot fi urmarite transformarile de stare, transformarile alotropice, variatiile solubilitatii etc., pentru toate aliajele din sistemul considerat.
Construirea diagramelor de echilibru se face experimental urmarindu-se transformarile ce se produc la incalzire si racire in conditii de echilibru, ale unui mare numar de aliaje dintr-un sistem dat. Temperaturile la care se produc diverse transformari (temperaturi critice) sunt puse in evidenta prin anomaliile ce apar pe curbele de variatie cu temperatura a anumitor proprietati. In timpul incalzirilor si racirilor lente, pot fi urmarite momentele in care pe curbele de racire apar discontinuitati (analiza termica), sau se produc modificari ale compactitatii retelei (analiza dilatometrica) sau apar modificari bruste ale rezistivitatii electrice (analiza electrica) sau ale proprietatilor magnetice (analiza magnetica).
Determinand punctele critice ale mai multor aliaje dintr-un sistem, transpunandu-le in coordonate temperatura - concentratie si unind familiile punctelor critice obtinute, vor rezulta diagramele de echilibru ale sistemului considerat.
Dispunand de aceste diagrame de echilibru, se vor putea stabili conditiile de elaborare ale oricarui aliaj, posibilitatea de aplicare a anumitor tratamente termice, precum si alegerea temperaturii optime pentru tratament termic, vor putea fa determinate fazele constituente precum si constituentii metalografici ai aliajelor, etc. Rezulta astfel importanta practica deosebita pe care o au aceste diagrame de echilibru.
1. Clasificarea sistemelor de aliaje binare
Aspectul diagramelor de echilibru binare este influentat de natura componentilor sistemului, de solubilitatea componentilor in stare lichida si in stare solida, precum si de posibilitatea aparitiei unor transformari fazice in stare solida.
2. Diagramele de echilibru ale sistemelor cu componenti insolubili atat in stare lichida cat si in stare solida
In conditiile in care, atomii componentilor unui aliaj aflat in stare lichida, nu se pot dizolva, ei se vor separa dupa densitatile lor, rezultand un lichid neomogen. Daca curentii de convectie care iau nastere in aceasta topitura nu sunt suficient de puternici, sau daca printr-o actiune mecanica (agitare, vibrare) nu se va proceda la amestecarea lichidelor metalice insolubile, metalul topit cu o densitate mai mare, se va separa Ia fundul creuzetului. Situatia se va pastra si dupa solidificarea aliajului, rezultand un material cu proprietati necorespunzatoare.
Pentru eliminarea acestei stratificari a metalelor topite insolubile, se poate proceda la agitarea mecanica sau vibrarea topiturilor. atat in timpul elaborarii cat si in timpul solidificarii aliajului. O alta metoda de obtinere a pieselor din astfel de aliaje, este aceea a metalurgiei pulberilor (amestecarea pulberilor metalice, presarea si sinterizarea lor).
In figura 6. este prezentata diagrama de echilibru a unui sistem cu componenti insolubili in stare lichida si solida, particularizandu-se diagrama pentru sistemul Fe-Pb La temperaturi superioare temperaturii TA , cele doua lichide metalice nu sunt miscibile. La temperatura TA , se va solidifica metalul A, pastrandu-se metalul B in stare lichida pana la temperatura TB , cand si acesta se va solidifica. In final se vor obtine cristale de metal pur A si cristale de metal pur B.
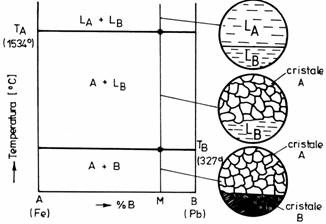
Figura 6. Diagrama de echilibru a unui sistem cu componenti insolubili in stare lichida si solida.
Diagramele de echilibru ale sistemelor cu componenti partial solubili in stare lichida si insolubili in stare solida
Un exemplu pentru un astfel de sistem este prezentat in figura 7, particularizandu-se diagrama pentru sistemul Pb-Zn.
In figura se observa ca in anumite intervale de temperatura si concentratie, componentii sunt solubili in stare lichida. La scaderea temperaturii in domeniul c-d-e-TB , se inregistreaza o separare a doua lichide LA si LB . Lichidul LA contine intr-o proportie mai mica si atomi ai componentului B, iar lichidul LB , invers. Nu vor rezulta deci lichide de metal pur A si de metal pur B, ceea ce inseamna ca in stare lichida componentii sunt partial solubili. Considerand aliajul M, la scaderea temperaturii cand este atinsa orizontala d-e, LA va avea compozitia punctului d, iar LB , compozitia punctului e. Pe masura ce scade temperatura, LA se va imbogati in atomi ai componentului A, iar LB in atomi de B. La temperatura de solidificare a componentului B, LA va avea concentratia punctului C, iar LB va avea concentratia de 100 % B. La temperatura TB , se vor forma cristale de metal pur B, iar odata cu scaderea in continuare a temperaturii, LA se va imbogati mai mult in atomi ai componentului A. La temperatura TA , LA va avea concentratia de 100 % A si va cristaliza, dand nastere unor cristale de metal pur A. Rezulta deci in urma solidificarii, un amestec mecanic de metale pure A si B.
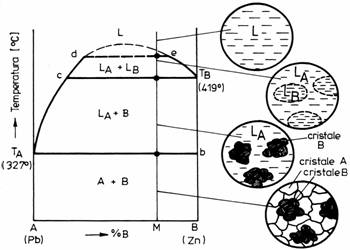
Figura 7. Diagrama de echilibru a unui sistem cu componenti partial solubili in stare lichida si insolubili in stare solida.
Liniile d-c-TA si e-TB se numesc linii de solubilitate in stare lichida, iar LA si LB se numesc solutii lichide conjugate. Linia TA-c-TB este linia lichidus a diagramei, linie peste care aliajele sistemului sunt in stare lichida. Linia TA-b-TB este linia solidus a sistemului, linie sub care toate aliajele sistemului sunt solidificate.
Pentru reducerea segregatiei gravitationale care se manifesta la aliajele din aceste sisteme, se recomanda vibrarea topiturilor pe toata durata solidificarii, precum si aplicarea unor viteze mari de racire.
4. Diagramele de echilibru ale sistemelor cu componenti complet solubili in stare lichida
4.1. Sisteme binare cu componenti complet solubili atat in stare lichida cat si in stare solida
Sistemele binare cu componenti complet solubili in stare lichida si in stare solida, se mai numesc si sisteme binare cu solutie solida totala, sau cu solutie solida izomorfa. Componentii aliajelor din aceste sisteme, se dizolva reciproc in orice proportie, rezultand dupa solidificare solutii solide de substitutie.
In figura 8. este prezentata diagrama de echilibru a unui sistem cu solutie solida totala (izomorfa), particularizandu-se diagrama pentru sistemul Cu-Ni. Considerand aliajul M, se observa ca la racirea lichidului omogen L, sub linia lichidus se vor forma in topitura cristale de solutie solida alfa acestea dezvoltandu-se pe masura ce scade temperatura. La atingerea curbei solidus, materialul va fi complet solidificat, rezultand o structura formata din graunti de solutie solida alfa.
Analizand microstructura aliajului rezultat, se constata ca grauntii de solutie solida nu prezinta omogenitate chimica pe sectiunea grauntelui, adica se evidentiaza fenomenul de segregatie intracristalina. Pentru explicarea aparitiei acestei segregatii, trebuie prezentata asa numita regula a orizontalei, regula utilizata in studiul diagramelor de echilibru.
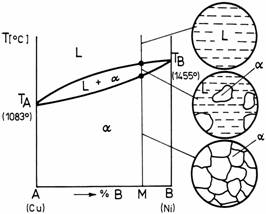
Figura 8. Diagrama de echilibru a unui sistem cu solutie solida totala.
4.2. Regula orizontalei
Regula orizontalei se aplica in studiul diagramelor de echilibru binare, pentru determinarea compozitiei chimice a fazelor aflate in echilibru la o anumita temperatura.
Compozitia chimica a fazelor in echilibru, este data de abscisa punctelor de intersectie a orizontalei de temperatura cu curbele de transformare ale diagramei de echilibru. Orice modificare a temperaturii in intervalul temperaturilor de solidificare (cuprins intre curba lichidus si curba solidus) schimba compozitia fazelor aflate in echilibru. In intervalul de transformare, compozitia fazei lichide evolueaza pe curba lichidus, iar cea a fazei solide, pe curba solidus.
Fie aliajul M din sistemul binar cu solutie solida izomorfa (fig. 9), incalzit la o temperatura superioara curbei lichidus. La scaderea temperaturii, in momentul cand este atinsa temperatura T1, in lichidul metalic vor lua nastere primii germeni de cristalizare. Trasand o orizontala Ia nivelul temperaturii T1, aceasta va intersecta curbele lichidus si solidus, pe fiecare intr-un punct. Proiectand pe axa concentratiilor aceste puncte, vor rezulta punctele M si alfa1 , punctul M va indica compozitia chimica a lichidului, iar punctul alfa1 - compozitia chimica a germenilor de cristalizare. Se observa ca germenii de cristalizare sunt de solutie solida cu o concentratie ridicata de atomi ai componentului B.
Odata cu scaderea temperaturii germenii de cristalizare se vor dezvolta, modificandu-se echilibrul dintre faze. La temperatura T2 , orizontala va intersecta curbele lichidus si solidus, proiectia punctelor de intersectie fiind l2 si alfa2 . Punctul l2 indica compozitia chimica a fazei lichide, iar punctul alfa2 indica compozitia chimica a fazei solide (cristalelor de solutie solida), la temperatura T2 . Se poate observa ca pe masura ce temperatura scade, concentratia de component B din cristale scade, iar concentratia de component A din lichid creste.
La temperatura T3 , este atinsa curba solidus. Orizontala trasata la aceasta temperatura, indica faptul ca grauntii au ajuns Ia compozitia chimica M, iar ultimele parti lichide ale aliajului care s-a solidificat, au avut compozitia chimica l3 . Presupunand deci ca in timpul solidificarii si racirii nu s-au manifestat difuzii ai atomilor componentilor A si B, grauntii vor prezenta in centrul lor compozitia chimica alfa1 , iar la suprafata lor compozitia chimica l3 . In realitate, datorita conditiilor reale in care se desfasoara procesul de solidificare si racire, atomii componentilor aliajului au posibilitatea de a difuza in sensul uniformizarii compozitiei chimice pe sectiunea grauntilor, astfel incat segregatia intracristalina se diminueaza. Cristalele astfel formate si care prezinta o segregatie intracristalina poarta denumirea de cristale zonare. Prin tratamentul termic de recoacere de omogenizare, segregatiile cristalelor zonale pot fi diminuate substantial.
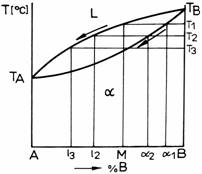
Figura 9. Regula orizontalei aplicate la o diagrama binara cu solutie solida izomorfa.
4. Regula parghiei
Pe langa regula orizontalei, in studiul diagramelor de echilibru este utilizata si regula parghiei. Cu ajutorul regulii parghiei, este posibila determinarea raportului cantitativ, care exista intre fazele aflate in echilibru Ia o anumita temperatura.
Intre curbele lichidus si solidus, aliajele prezinta un amestec de doua faze, respectiv una solida si alta lichida, raportul dintre cantitatea de solid si cea de lichid variind cu temperatura. La temperaturi apropiate de T1 (fig. 9), cantitatea de solid este foarte mica, iar cea de lichid foarte mare, iar la temperaturi apropiate de T3 , cantitatea de faza solida este foarte mare, pe cand cea de lichid este redusa. Cantitatea fazelor solide si lichide, existente la o anumita temperatura, poate fi determinata cu ajutorul regulii parghiei.
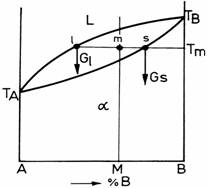
Figura 10. Regula parghiei aplicata la o diagrama binara cu solutie solida izomorfa.
Referindu-ne la figura 10, se presupune ca dorim sa determinam cantitatea de lichid si solid a aliajului M, aflat la temperatura Tm . Notam intersectia dintre verticala concentratiei M si orizontala temperaturii Tm , cu "m". Orizontala trasata prin punctul "m", intersecteaza curba lichidus in punctul "l" , iar curba solidus in "s". Aliajul aflandu-se in echilibru, punctul "m" poate fi considerat ca punct de sprijin al parghiei "ls", parghie aflata si ea in echilibru sub actiunea greutatii lichidului Gl si a solidului Gs. Ecuatia momentelor acestei parghii este:
![]() de unde:
de unde: ![]() Gl/Gs = sm/lm
Gl/Gs = sm/lm
Rezulta ca greutatea fazei lichide este proportionala cu segmentul "sm", iar greutatea fazei solide cu segmentul "lm". Daca se imparte parghia "ls" in 100 de diviziuni, respectiv 100 %, segmentul "sm" va exprima procentual cantitatea de lichid, iar segmentul "lm", cantitatea de solid. Din acest motiv regula parghiei mai poarta denumirea de regula segmentelor inverse.
4.4. Sisteme binare cu componenti solubili in stare lichida si insolubili in stare solida
a) Diagrama cu eutectic
Un exemplu pentru o diagrama cu eutectic, dintr-un sistem cu componenti insolubili in stare solida si solubili in stare lichida, este prezentat in figura 11, particularizandu-se diagrama pentru sistemul Pb-Sb.
Feste curba lichidus TA-e-TB , aliajele se gasesc in stare lichida, topiturile fiind omogene. Sub linia solidus TA-a-e-b-TB , aliajele sistemului sunt complet solidificate, prezentand o structura formata din doua faze, respectiv metal pur A si metal pur B, componentii fiind insolubili in stare solida. Se va urmari in continuare procesul de solidificare al aliajului: M (67 % B, 33 % A). La scaderea temperaturii, la atingerea curbei lichidus, in lichidul omogen L vor apare primii germeni de cristalizare. Aplicand regula orizontalei in punctul acesta, se constata ca germenii care s-au format in topitura, sunt de metal pur B. Odata cu scaderea temperaturii, va continua separarea de cristale de metal pur B din topitura si astfel compozitia chimica a lichidului metalic se va modifica continuu, tinzand catre concentratia corespunzatoare punctului "e".
Punctul "e" se numeste punct eutectic, si el este determinat de o temperatura eutectica si o concentratie eutectica. Lichidul cu concentratia eutectica se va solidifica la temperatura constanta, dand nastere unui amestec mecanic eutectic. Fazele componente ale acestui amestec mecanic pot fi determinate prin aplicarea regulii orizontalei in punctul eutectic "e". Orizontala dusa in "e" atinge in partea stanga ordonata metalului pur A, iar in dreapta, pe cea a metalului pur B, rezulta deci ca amestecul mecanic eutectic este format din cristale fine de metal pur A si de metal pur B. In final aliajul M va prezenta o structura formata din cristale de metal pur B (care s-au format la temperaturi superioare temperaturii eutectice) si eutectic E (format la temperatura eutectica).
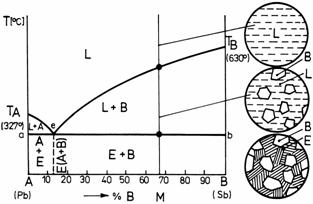
Figura 11. Diagrama de echilibru cu eutectic pentru un sistem binar cu componenti solubili in stare lichida si insolubili in stare solida
Cristalizarea lichidului cu concentratie eutectica poate fi exprimata prin relatia:
![]()
adica lichidul cu concentratia "e" se transforma la racire intr-un amestec mecanic eutectic format din cristale de A (cu concentratia "a") si cristale de B (cu concentratia "b"). La incalzire transformarea este inversa.
Aliajele care cristalizeaza dupa o diagrama cu eutectic, pot fi clasificate in aliaje hipoeutectice (in stanga punctului eutectic); eutectice si hipereutectice (in dreapta punctului eutectic). Aliajul M este deci un aliaj hipereutectic. Urmarind cristalizarea unui aliaj hipoeutectic se constata ca dupa solidificarea acestuia, structura rezultata va fi formata din cristale de metal pur A si eutectic B.
Pentru determinarea rapida a raportului cantitativ dintre fazele constituente ale unui aliaj, respectiv dintre constituentii metalografici, sub diagramele de echilibru pot fi construite diagramele de faze si de constituenti (fig. 12). In figura s-a prezentat pentru aliajul M, proportiile fazelor A si B, precum si proportiile constituentilor E si B la temperatura ordinara.
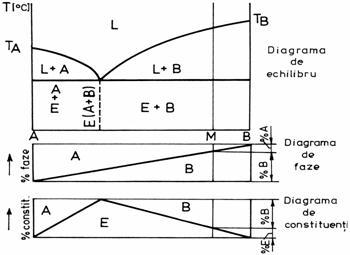
Figura 12. Diagramele de faze si de constituenti intr-un sistem binar cu eutectic.
Diagramele de faze sunt deosebit de utile pentru aprecierea proprietatilor unui aliaj aflat in stare de echilibru. Fiecarei faze ii sunt proprii anumite proprietati si cunoscand raportul dintre fazele constituente ale unui aliaj, precum si proprietatile fiecarei faze, pot fi apreciate proprietatile aliajului.
Cu ajutorul diagramelor de constituenti poate fi determinata cu aproximatie compozitia chimica a aliajelor aflate in stare de echilibru. In timpul cercetarii microscopice se apreciaza suprafata ocupata de constituenti si considerand ca densitatile constituentilor sunt egale, pe diagrama de constituenti se va determina compozitia chimica a aliajului.
b) Diagrama cu compus chimic stabil
Acest gen de diagrame de echilibru apar in sistemele in care la o anumita compozitie chimica se formeaza un compus chimic stabil AmBn , care nu se poate dizolva in componentii A si B. In figura 13 este prezentat un exemplu pentru o astfel de diagrama.
Temperaturile de topire ale compusilor chimici sunt in general superioare temperaturilor de topire a celor doi componenti. Compusul chimic are o concentratie fixa si se reprezinta in diagrama printr-o verticala trasata in dreptul concentratiei sale, limitata la partea superioara de temperatura sa de topire. Aceasta verticala imparte diagrama de echilibru in doua diagrame simple cu eutectic.
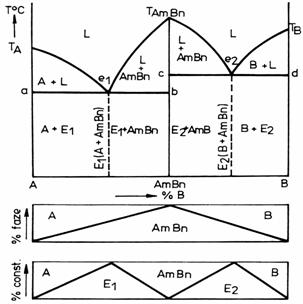
Figura 1 Diagrama de echilibru cu compus chimic pentru un sistem binar cu componenti solubili in stare in stare lichida si insolubili in stare solida.
In diagrama apar deci doua transformari eutectice:
![]()
![]()
Campurile diagramei se completeaza, utilizand regula orizontalei aplicata in fiecare domeniu. Sub diagrama de echilibru sunt prezentate si diagramele de faze si constituenti.
c) Diagrame cu punct peritectic
O diagrama cu componenti insolubili in stare solida, care prezinta un punct peritectic este prezentata in figura 14.
In aceasta diagrama apare un compus chimic AmBn care este stabil Ia incalzire pana Ia atingerea temperaturii corespunzatoare orizontalei c-d-f. La temperaturi superioare acestei orizontal e, compusul chimic se descompune in doua faze, respectiv in lichid de concentratie "c" si cristale de metal pur B. Aceasta transformare este cunoscuta sub denumirea de transformare peritectica si ea se produce la traversarea orizontalei peritectice c-d-f.
Punctul de inflexiune "c" care apare pe curba lichidus, la extremitatea orizontalei peritectice poarta denumirea de punct peritectic.
Transformarea peritectica se produce astfel:
![]()
In diagrama prezentata se evidentiaza si punctul eutectic "e". Transformarea eutectica se produce astfel:
![]()
Campurile diagramei precum si diagramele de faze si de constituenti se completeaza prin metodele aratate anterior, aplicand in fiecare camp, regula orizontalei.
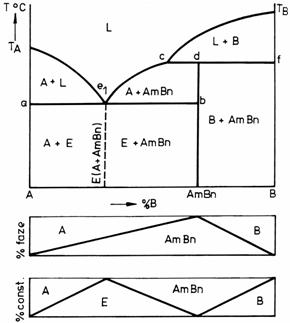
Figura 14. Diagrama de echilibru cu punct peritectic pentru un sistem binar cu componenti solubili in stare lichida si insolubili in stare solida.
4.5. Sisteme binare cu componenti solubili in stare lichida si partial solubili in stare solida
In cazul in care diametrele atomilor componentilor A si B sunt apropiate ca marime, iar valentele sunt egale sau apropiate, dar tipul retelelor cristaline este diferit, este de asteptat ca in stare lichida componentii sa se dizolve complet unul in altul, iar in stare solida fiecare component sa dizolve o anumita cantitate a celuilalt component, solubilitatea in stare solida ramanand insa limitata. Iau nastere astfel, sistemele cu componenti partial solubili in stare solida. Dintre aceste sisteme fac parte acelea care formeaza diagrame cu eutectic, cu compus chimic si cu peritectic.
a) Diagrame cu eutectic
In figura 15 sunt prezentate diagramele de echilibru cu eutectic ale sistemelor cu componenti complet solubili in stare lichida si partial solubili in stare solida. In cazul "a" solubilitatea componentilor nu variaza cu temperatura, iar in cazul "b" solubilitatea componentilor variaza cu temperatura.
Dupa cum se observa din diagrame, in anumite intervale ale concentratiei se formeaza solutii solide, respectiv solutia solida alfa (solvent A, dizolvat B) si solutia solida beta (solvent B, dizolvat A). In intervalele A-c si B-d, aliajele sunt monofazice, iar in intervalul de concentratii c-d aliajele sunt bifazice. In ambele diagrame transformarea eutectica se produce astfel:
![]()
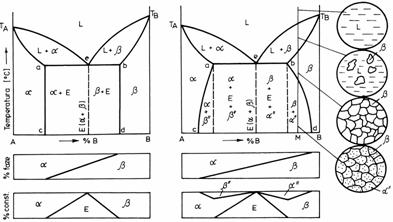
Figura 15. Diagrame de echilibru cu eutectic pentru un sistem binar cu componenti solubili in stare lichida si partial solubili in stare solida: a) solubilitatea componentilor nu variaza cu temperatura; b) solubilitatea componentilor variaza cu temperatura.
deci amestecul mecanic eutectic este constituit din doua solutii solide (alfa si beta).
In cazul diagramei prezentate in figura 15.b, apar suplimentar doua curbe a-c si b-d, curbe care indica solubilitatea variabila a componentilor in functie de temperatura. In lungul curbei a-c, la scaderea temperaturii, din solutia solida alfa care devine suprasaturata, se separa faza beta", iar in lungul curbei b-d, din solutia solida beta suprasaturata, se va separa faza alfa".
In figura, alaturi de diagrama de echilibru este prezentat modul de formare a structurii la solidificare si racire, a aliajului hipereutectic M.
Solutiile solide precipitate in stare solida datorita variatiei solubilitatii cu temperatura poarta denumirea de solutii solide secundare. Precipitarea acestor solutii solide secundare vor influenta puternic proprietatile aliajelor in sensul ca prin marirea tensiunilor interne este determinata cresterea duritatii si a rezistentei la rupere, precum si scaderea plasticitatii aliajelor. Cantitatea constituentilor secundari precipitati la racirea lenta a unui aliaj, poate fi determinata pe diagramele de constituenti.
b) Diagrame cu compus chimic
In figura 16. sunt prezentate doua diagrame cu compus chimic cu componenti solubili in stare lichida si partial solubili in stare solida. In stanga este prezentat cazul cand solubilitatea nu variaza cu temperatura, iar in dreapta, cazul cand solubilitatea variaza cu temperatura.
Compusul chimic intermetalic care apare in aceste diagrame (AmBn ) are posibilitatea de a dizolva atat component A cat si component B. El este deci capabil sa formeze solutii solide, AmBn jucand rolul de solvent, iar componentii A si B, de dizolvat. Aceasta solutie solida a fost notata in diagramele prezentate cu gama.
Diagramele de echilibru din figura 16 prezinta doua puncte eutectice, transformarile eutectice fiind urmatoarele:
![]()
![]()
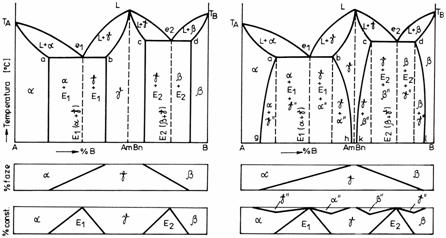
Figura 16. Diagrama de echilibru cu compus chimic pentru sisteme binare cu componenti solubili in stare lichida si partial solubili in stare solida: a) solubilitatea componentilor nu variaza cu temperatura; b) solubilitatea componentilor variaza cu temperatura.
In cazul in care solubilitatea componentilor variaza cu temperatura, din solutiile solide suprasaturate vor precipita la scaderea temperaturii constituentii secundari (alfa", beta", gama").
c) Diagrame cu punct peritectic
Caracteristic pentru acest tip de diagrame este faptul ca aliajele situate intr-un anumit interval de concentratie sufera o transformare peritectica. In figura 17 sunt prezentate doua diagrame cu punct peritectic, in cazul a) solubilitatea componentilor nu variaza cu temperatura, iar in cazul b) solubilitatea variaza cu temperatura.
Aliajele cu compozitii chimice situate in stanga punctului "a" si in dreapta punctului "c", cristalizeaza cu formarea de solutii solide alfa si beta. Aliajele cu compozitii chimice cuprinse intre punctele "a" si "c" vor suferi o transformare peritectica.
Se considera aliajul M incalzit la o temperatura superioara curbei lichidus. In timpul racirii, la atingerea liniei lichidus, din lichid se vor separa cristale de solutie solida beta, care se vor dezvolta pe masura ce temperatura scade. In timpul racirii compozitia chimica a lichidului variaza dupa curba TB-a, iar compozitia chimica a solidului, dupa curba TB-c. La atingerea temperaturii corespunzatoare orizontalei peritectice se va produce transformarea peritectica:
![]()
Deci, din unirea celor doua faze aflate la extremitatile orizontalei peritectice, a luat nastere o faza noua, respectiv solutia solida alfa. La transformarea peritectica, doar o parte a cristalelor de solutie solida beta vor contribui la formarea solutiei solide alfa, cele ramase in exces isi vor pastra individualitatea si la temperaturi inferioare orizontalei peritectice. Astfel la o temperatura aflata imediat sub orizontala peritectica, aliajul M prezinta o structura formata din cristale de s.s.alfa si de s.s.beta. In cazul in care solubilitatea componentilor variaza cu temperatura, in lungul curbelor d-b si e-c, vor precipita din solutiile solide suprasaturate, constituentii secundari beta" si alfa". La temperatura ambianta aliajul M va prezenta deci o structura formata din patru constituenti: alfa, alfa", beta, beta". Proportia fazelor constituente poate fi determinata pe diagrama de faze, iar proportia constituentilor pe diagrama de constituenti.
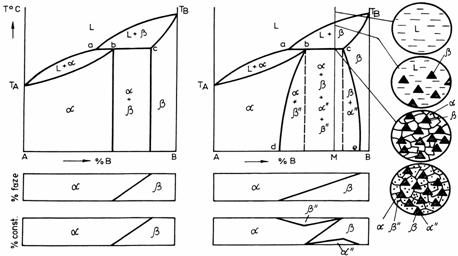
Figura 17. Diagrame de echilibru cu punct peritectic pentru sisteme binare cu componenti solubili in stare lichida si partial solubili in stare solida: a) solubilitatea componentilor nu variaza cu temperatura; b) solubilitatea variaza cu temperatura.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








