
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Echilibrul rigidului supus la legaturi cu frecare |
Echilibrul rigidului supus la legaturi cu frecare
Tabelul 1
Frecarea este fenomenul complex fizico-mecanic prin care se intelege rezistenta opusa de legaturile unui solid la deplasarile acestuia, deplasari care pot fi: alunecare, rostogolire, pivotare.
Aspectul general al frecarilor in cazul reazemului simplu.
Se considera un corp care are un
reazem simplu in O.
Teoretic exista un singur
punct de contact, in realitate
insa sub actiunea fortelor ![]() corpul considerat se deformeaza in asa fel incat contactul se
realizeaza pe o mica suprafata (fig. 39a).
corpul considerat se deformeaza in asa fel incat contactul se
realizeaza pe o mica suprafata (fig. 39a).
|
a) b) c) Fig: 39 |
In fiecare punct al
acestei suprafete se
dezvolta o reactiune de marime si directie necunoscuta pe care o notam in general cu ![]() . Se considera punctul
teoretic de contact (in care ar
fi avut loc contactul celor doua corpuri
daca ele nu
s-ar fi deformat). Torsorul in O al fortelor de legatura
. Se considera punctul
teoretic de contact (in care ar
fi avut loc contactul celor doua corpuri
daca ele nu
s-ar fi deformat). Torsorul in O al fortelor de legatura ![]() aplicate in Ai
este alcatuit din:
aplicate in Ai
este alcatuit din:
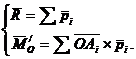
Reducand sistemul de forte ![]() si de reactiuni
si de reactiuni ![]() in punctul O, (fig. 39b) se obtin in cazul echilibrului,
ecuatiile:
in punctul O, (fig. 39b) se obtin in cazul echilibrului,
ecuatiile:
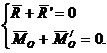
Proiectand relatiile (148) pe normala la suprafata de contact si pe planul tangent la aceasta suprafata se obtine:
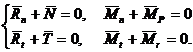
In baza teoremei de
echivalenta rezulta ca sistemul de forte ![]() este echivalent cu doua forte
este echivalent cu doua forte ![]() si
si ![]() aplicate in O si doua cupluri de momente
aplicate in O si doua cupluri de momente ![]() si
si ![]() iar sistemul de reactiuni
iar sistemul de reactiuni ![]() este echivalent cu doua forte
este echivalent cu doua forte ![]() si
si ![]() aplicate deasemenea in O si cu doua cupluri de momente
aplicate deasemenea in O si cu doua cupluri de momente ![]() si
si ![]() .
.
Forta ![]() tinde sa deplaseze
corpul in directia normala la suprafata de contact,
deplasare impiedicata de reactiunea normala
tinde sa deplaseze
corpul in directia normala la suprafata de contact,
deplasare impiedicata de reactiunea normala ![]() .
.
Forta ![]() tinde sa deplaseze corpul in planul tangent la
suprafata de
sprijin, aceasta deplasare
poarta numele de alunecare si este impiedicata de reactiunea
tinde sa deplaseze corpul in planul tangent la
suprafata de
sprijin, aceasta deplasare
poarta numele de alunecare si este impiedicata de reactiunea ![]() care poarta numele de forta de frecare de alunecare.
care poarta numele de forta de frecare de alunecare.
Cuplul de moment ![]() are tendinta de a roti
corpul in jurul
normalei la suprafata de
contact, o asemenea rotatie poarta numele de pivotare si este impiedicata de cuplul de
moment
are tendinta de a roti
corpul in jurul
normalei la suprafata de
contact, o asemenea rotatie poarta numele de pivotare si este impiedicata de cuplul de
moment ![]() , numit cuplu de
frecare de pivotare.
, numit cuplu de
frecare de pivotare.
Cuplul de moment ![]() are tendinta de a roti corpul in jurul unei axe din
planul tangent la suprafata de
contact. O asemenea rotatie poarta numele de rostogolire si este impiedicata de cuplul de
moment
are tendinta de a roti corpul in jurul unei axe din
planul tangent la suprafata de
contact. O asemenea rotatie poarta numele de rostogolire si este impiedicata de cuplul de
moment ![]() , denumit cuplu de
frecare de rostogolire.
, denumit cuplu de
frecare de rostogolire.
In cele ce urmeaza se vor analiza detailat fiecare din tipurile de frecare.
2) Frecarea de alunecare
Consideram un solid (S) aflat pe o suprafata plana. Atunci cand asupra solidului actioneaza numai greutatea
acestuia, ei i se opune reactiunea
normala ![]() . Cand asupra
solidului actioneaza si o forta orizontala
. Cand asupra
solidului actioneaza si o forta orizontala ![]() pentru a se mentine echilibrul este
necesar ca rezultanta fortelor de legatura
pentru a se mentine echilibrul este
necesar ca rezultanta fortelor de legatura ![]() sa fie egala si direct opusa cu rezultanta fortelor active
sa fie egala si direct opusa cu rezultanta fortelor active ![]() :
:
![]()
|
a) b) Fig: 40 |
Se noteaza cu a unghiul format de rezultanta fortelor de legatura cu suportul reactiunii normale (unghi de aderenta). Ecuatia de echilibru (150), poate fi scrisa scalar:
![]()
sau
![]()
Marind forta ![]() se observa ca solidul ramane in repaus pana la o valoare limita a acesteia
se observa ca solidul ramane in repaus pana la o valoare limita a acesteia ![]() (fig. 40b). Forta limita corespunde unei stari limita pentru
care
(fig. 40b). Forta limita corespunde unei stari limita pentru
care ![]() . Starea limita de
echilibru la alunecare este starea mecanica caracterizata prin echilibrul
sistemului de forte aplicate si de legatura si de iminenta alunecarii.
. Starea limita de
echilibru la alunecare este starea mecanica caracterizata prin echilibrul
sistemului de forte aplicate si de legatura si de iminenta alunecarii.
![]()
sau
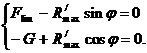
![]()
unde ![]() este coeficientul de
frecare de alunecare.
este coeficientul de
frecare de alunecare.
Dintre experientele facute asupra fortelor de frecare de alunecare se remarca cele facute de Coulomb, care au condus la legile frecarii uscate:
marimea fortei de frecare de alunecare maxima este direct proportionala cu marimea reactiunii normale;
marimea fortei de frecare de alunecare depinde de natura si starea corpurilor in contact;
marimea fortei de frecare de alunecare nu depinde de viteza relativa de deplasare a celor doua corpuri si nici de marimea suprafetelor in contact.
Pe baza acestor legi, forta de frecare de alunecare are expresia:
![]()
Observatii asupra legilor lui Coulomb:
a)
Forta de frecare de
alunecare nu este preexistenta tendintei de alunecare (forta ![]() )
)
b)
Forta de frecare de
alunecare ia valori cuprinse intre zero si o valoare maxima ![]() .
.
c) Forta de frecare de alunecare are directia tendintei de alunecare si sens invers acesteia.
Rotind suportul fortei limita intr-un plan perpendicular pe suportul greutatii in punctul P, unghiul j pastandu-se constant, suportul reactiunii maxime va descrie suprafata unui con numit con de frecare, conditia de echilibru fiind in acest caz ca rezultanta fortelor active sa se gaseasca in interiorul sau pe generatoarea conului de frecare.
3) Frecarea de rostogolire
|
a) b) c) d) Fig: 41 |
La inceputul acestui
subcapitol s-a aratat ca frecarea de
rostogolire se manifesta printr-un
cuplu de moment ![]() Se considera exemplul concret al
unei roti trase.
Se considera exemplul concret al
unei roti trase.
Sa presupunem ca se realizeza contactul intre roata si planul orizontal intr-un singur punct (fig: 41a). Necesitatea de a se tine seama rezulta imediat, deoarece ramanand la ipoteza unui contact punctual in A, in acest punct nu se pot introduce decat reactiunea normala N si forta de frecare T, iar ecuatiile de echilibru devin:
![]()
Din ultima relatie rezulta F=0,
rezultat care contrazice experienta care arata ca roata poate ramane in repaus chiar daca asupra ei actioneaza o forta F orizontala, cu conditia insa ca modulul acestei
forte sa nu depaseasca o anumita limita. Din cauza
deformabilitatii
contactul intre roata si calea de rulare se face pe o mica suprafata (fig. 41b), pe care
apar reactiuni
normale ![]() si reactiuni tangentiale
si reactiuni tangentiale ![]() (datorate frecarii de alunecare).
Suportul rezultantei
(datorate frecarii de alunecare).
Suportul rezultantei ![]() a reactiunilor
normale
a reactiunilor
normale ![]() se afla in general la o distanta e de punctul teoretic de contact
A. In timp ce suportul
rezultantei
se afla in general la o distanta e de punctul teoretic de contact
A. In timp ce suportul
rezultantei ![]() al reactiunilor
al reactiunilor ![]() poate fi considerat cu o foarte buna aproximatie ca trece prin A. Daca in punctul A se introduc doua forte egale si direct opuse, avand modulul N (fig. 41c), se observa ca fortele de legatura sunt echivalente cu
fortele
poate fi considerat cu o foarte buna aproximatie ca trece prin A. Daca in punctul A se introduc doua forte egale si direct opuse, avand modulul N (fig. 41c), se observa ca fortele de legatura sunt echivalente cu
fortele ![]() si
si ![]() aplicate in A
(ca si cum nu ar
exista deformatii) si cu un cuplu de
frecare de rostogolire de moment Mr=Ne
(fig. 41d). Scriind ecuatiile de
echilibru in aceasta situatie se obtine:
aplicate in A
(ca si cum nu ar
exista deformatii) si cu un cuplu de
frecare de rostogolire de moment Mr=Ne
(fig. 41d). Scriind ecuatiile de
echilibru in aceasta situatie se obtine:
|
![]()
|
a) b) c) Fig: 42 |
Deoarece echilibrul nu
are loc decat pentru
valori limitate ale modulului fortei F, rezulta ca ![]() si deci momentul Mr este limitat. Cum insa Mr=Ne
si N=G, rezulta ca, de fapt distanta e este limitata. Daca se noteaza emax=s, rezulta ca pentru echilibru este
mecesar sa avem:
si deci momentul Mr este limitat. Cum insa Mr=Ne
si N=G, rezulta ca, de fapt distanta e este limitata. Daca se noteaza emax=s, rezulta ca pentru echilibru este
mecesar sa avem:
![]()
Prin analogie cu frecarea de alunecare, marimea s s-a numit coeficient de frecare de rostogolire si reprezinta distanta maxima cu care se deplaseaza paralel cu el insusi suportul reactiunii normale N fata de punctul teoretic de contact A. Coeficientul de frecare de rostogolire are dimensiunea unei lungimi, valoarea sa depinzand in special de raza rotii si natura materialului. In problemele de frecare de rostogolire intervin atat cuplul de frecare de rostogolire cat si forta de frecare de alunecare, de aceea este necesar atunci cand se scriu conditiile de echilibru, pe langa inegalitate (159) sa se tina seama si de inegalitatea (156) cunoscuta de la frecarea de alunecare.
4) Frecarea de pivotare
Asa cum s-a aratat la inceputul acestui subcapitol frecarea de pivotare se manifesta printr-un cuplu de moment Mp.
Se considera un arbore vertical de
sectiune
transversala inelara ce se sprijina intr-un lagar. Daca se presupune
coeficientul de frecare de alunecare ![]() intre arbore
si lagar, acelasi intre toate punctele de
contact, iar presiunea p aceiasi pe toata suprafata de rezemare (fig.
42), si notand cu R si r cele doua raze ale coroanei
circulare iar cu N reactiunea normala totala, rezulta presiunea:
intre arbore
si lagar, acelasi intre toate punctele de
contact, iar presiunea p aceiasi pe toata suprafata de rezemare (fig.
42), si notand cu R si r cele doua raze ale coroanei
circulare iar cu N reactiunea normala totala, rezulta presiunea:
![]()
Reactiunea normala pe elementul de arie dA este pdA, iar forta de
frecare corespunzatoare,
tangenta la un cerc
de raza r ![]() si dirijata in sens invers sensului
de miscare va fi
si dirijata in sens invers sensului
de miscare va fi ![]() Momentul dat de aceasta forta elementara de frecare in raport cu
centrul O va fi
Momentul dat de aceasta forta elementara de frecare in raport cu
centrul O va fi ![]() Momentul cuplului de
frecare de pivotare va fi suma acestor momente elementare adica, folosind
coordonatele polare
Momentul cuplului de
frecare de pivotare va fi suma acestor momente elementare adica, folosind
coordonatele polare ![]() , vom avea succesiv:
, vom avea succesiv:
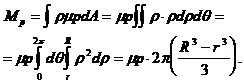
Inlocuind presiunea p cu expresia (161), rezulta momentul cuplului de frecare de pivotare sub forma:
![]()
In cazul sectiunii circulare facand r=0 in formula de mai sus, se obtine expresia:
![]()
5) Frecarea in articulatii si lagare
In afara cazurilor de frecare studiate pana aici, in tehnica mai sunt intalnite si alte cazuri importante cand intervine frecarea. Un astfel de caz il constituie frecarea ce apare in articulatii sau lagare. Se va studia numai frecarea uscata introducerea lubrifiantilor schimband esential problema. Se considera cazul lagarului cu joc, contactul avand loc teoretic numai intr-un punct A (fig. 43).
|
Fig: 43 |
Torsorul fortelor exterioare in O (pe axa) arborelului este alcatuit din ![]() si
si ![]() Vectorul
Vectorul ![]() fiind dirijat dupa axa arborelui are
tendinta sa imprime arborelului o
miscare de
rotatie. Actiunii momentului
fiind dirijat dupa axa arborelui are
tendinta sa imprime arborelului o
miscare de
rotatie. Actiunii momentului ![]() i se opune momentul de
frecare din lagar
i se opune momentul de
frecare din lagar ![]() . In punctul A are loc de fapt loc un fenomen de
frecare de alunecare si unul de
rostogolire. Torsorul fortelor de legatura este alcatuit din reactiunea normala
. In punctul A are loc de fapt loc un fenomen de
frecare de alunecare si unul de
rostogolire. Torsorul fortelor de legatura este alcatuit din reactiunea normala ![]() , forta de
frecare de alunecare
, forta de
frecare de alunecare ![]() si momentul
de frecare de rostogolire
si momentul
de frecare de rostogolire ![]() Notand cu r raza fusului
se obtin ecuatiile de echilibru:
Notand cu r raza fusului
se obtin ecuatiile de echilibru:
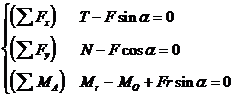
![]()
Din relatia (164) se obtin: T=Fsina N=Fcosa Mr=MO-Frsina care introduse in (165), conduc la conditiile de echilbru:
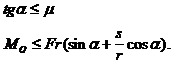
Pentru o buna functionare a masinilor se urmareste ca frecarea in lagare sa fie mica, adica ![]() are valori mici. In cazul
echilibrului la limita,
are valori mici. In cazul
echilibrului la limita, ![]() .
.
Unghiul a fiind mic se pot face aproximatiile:
![]()
Cu ajutorul relatiilor (167) se obtine din (166)
![]()
Notand acum coeficientul de frecare in lagar:
![]()
se obtine
![]()
Conform principiului
actiunii si reactiunii momentul de
frecare din articulatie (lagar) ![]() este egal si direct
opus lui
este egal si direct
opus lui ![]() . Analog forta
. Analog forta ![]() este egala si direct opusa lui
este egala si direct opusa lui ![]() care se stie ca se descompune in plan in doua componente H si V si in spatiu in trei componente Rx, Ry, Rz.
Tinand seama de acestea se
obtin
expresiile momentului de frecare in articulatii:
care se stie ca se descompune in plan in doua componente H si V si in spatiu in trei componente Rx, Ry, Rz.
Tinand seama de acestea se
obtin
expresiile momentului de frecare in articulatii:
in articulan articulatii si lagare cilindrice
![]()
in articulatii sferice
![]()
In cazul lagarului fara joc se obtin rezultate asemanatoare, pentru calculului momentului de frecare, utilizadu-se tot formulele (171) si (172).
6) Frecarea firelor
Un alt caz de frecare important in tehnica il constituie frecarea firelor. Aceasta frecare apare atat in cazul cand roata pe care este infasurat firul este fixa si firul are tendinta de miscare cat si in cazul cand firul este fix si roata are tendinta de miscare. In studiul firelor se face ipoteza ca acestea sunt flexibile, inextensibile si de greutate neglijabila
|
Fig: 44 |
Se considera in (fig. 44) un fir
care vine in contact
cu un disc fix pe arcul MN avand unghiul
la centru q (ma![]() . Se studiaza echilibrul
arcului elementar carui ii corespunde unghiul
la centru dq si care este actionat de tensiunile T si T+dT, de reactiunea
normala N si de forta de frecare de
alunecare care are valoarea limita
. Se studiaza echilibrul
arcului elementar carui ii corespunde unghiul
la centru dq si care este actionat de tensiunile T si T+dT, de reactiunea
normala N si de forta de frecare de
alunecare care are valoarea limita ![]() . Ecuatiile de
echilibru pentru cazul limita cand forta de frecare de
alunecare are valoare maxima sunt:
. Ecuatiile de
echilibru pentru cazul limita cand forta de frecare de
alunecare are valoare maxima sunt:
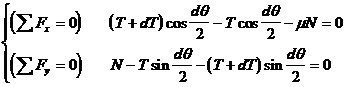
Fiind unghiuri mici se poate face aproximarea:
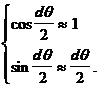
si rezulta
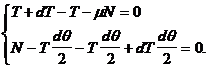
Termenul ![]() este neglijabil in comparatie cu ceilalti termeni si in consecinta se obtine sistemul de ecuatii:
este neglijabil in comparatie cu ceilalti termeni si in consecinta se obtine sistemul de ecuatii:
![]()
Din (150) se obtine o ecuatie diferentiala cu variabile separabile, care conduce la:
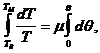
de unde se deduce pentru cazul limita studiat:
![]()
unde e=2,71828. De aici rezulta formula lui Euler pentru frecarea firelor:
![]() .
.
17 Aplicatii
Aplicatia 1
|
Fig: 45 |
Un corp de greutate P este legat prin intermediul unui cablu de inelul M de masa neglijabila (fig. 45) de inel se leaga cablurile AM si BM fixate in peretii verticali in punctele A si B. Sa se determine fortele care se aplica cablurilor AM si BM.
Rezolvare
In punctul M
actiunea
corpului de greutate ![]() se reprezinta prin
vectorul
se reprezinta prin
vectorul ![]() . Descompunem forta
. Descompunem forta ![]() conform regulii paralelogramului, pe directiile AM si BM. Se obtin fortele aplicate celor doua cabluri
conform regulii paralelogramului, pe directiile AM si BM. Se obtin fortele aplicate celor doua cabluri ![]() si
si ![]() care au directiile si sensurile cunoscute.
Pentru a obtine marimile lor se aplica teorema sinusului in unul din
triunghiurile care se formeaza cu cele
trei forte, avand in vedere si faptul ca
care au directiile si sensurile cunoscute.
Pentru a obtine marimile lor se aplica teorema sinusului in unul din
triunghiurile care se formeaza cu cele
trei forte, avand in vedere si faptul ca ![]()
(a) 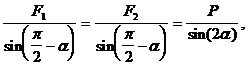
iar din relatia de mai sus va rezulta:
(b) ![]()
Aplicatia 2
Greutatea ![]() este sustinuta prin sistemul de
cabluri AM, BM si bara CM (fig. 46a). Bara se prinde in peretele vertical
astfel incat in lipsa legaturii comune in punctul M cade orientandu-se vertical, reactionand prin urmare numai
pe directia CM. Sa se determine fortele aplicate in M
cablurilor si barei.
este sustinuta prin sistemul de
cabluri AM, BM si bara CM (fig. 46a). Bara se prinde in peretele vertical
astfel incat in lipsa legaturii comune in punctul M cade orientandu-se vertical, reactionand prin urmare numai
pe directia CM. Sa se determine fortele aplicate in M
cablurilor si barei.
|
a) b) Fig: 46 |
|
Fig: 46c |
Rezolvare
Forta ![]() se descompune mai intai pe directiile MC si MC1
(fig. 46b). Se obtin:
se descompune mai intai pe directiile MC si MC1
(fig. 46b). Se obtin:
(a) ![]() si
si ![]()
Se descompune apoi forta R12 pe directiile MA si MB (fig. 46c). Se obtin:
(b) ![]()
O alta solutie este cea analitica, pentru aceasta se alege sistemul de axe xMyz (ca in fig. 46a). Relatia de echilibru va fi urmatoarea:
(c) ![]()
Proiectand pe axe relatia de mai sus rezulta
(d) 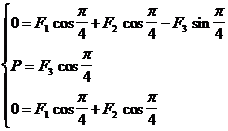
Din rezolvarea sistemului (d) se obtine:
(e) 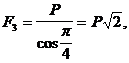
si
(f) ![]()
Aplicatia 3
|
Fig: 47 |
Sistemul de forte din figura 47 actioneaza asupra unui cub de latura a, stiind ca
![]()
si ca: ![]() se cere:
se cere:
a) Sa se calculeze momentele fortelor in raport cu punctul O;
b)
Cu ce este
echivalent sistemul format din fortele: ![]()
c)
Cu ce este
echivalent sistemul format din fortele: ![]()
d)
Cu ce este
echivalent sistemul format din fortele: ![]()
e)
Cu ce este
echivalent sistemul format din fortele: ![]()
f)
Cu ce este
echivalent sistemul format din fortele: ![]()
Rezolvare
a)
Notand cu ![]() momentul fortei
momentul fortei ![]() in raport cu
punctul O avem:
in raport cu
punctul O avem:
![]()
b) Torsorul de reducere in punctul O este:
![]()
Deci sistemul de forte paralele ![]() este echivalent cu zero.
este echivalent cu zero.
c) Torsorul de reducere in punctul O este:
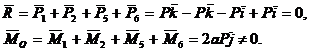
Sistemul de forte coplanare ![]() este deci echivalent cu un cuplu de moment 2aP, situat intr-un plan
perpendicular pe axa Oy. El poate fi
considerat ca un sistem de cupluri format din cuplurile
este deci echivalent cu un cuplu de moment 2aP, situat intr-un plan
perpendicular pe axa Oy. El poate fi
considerat ca un sistem de cupluri format din cuplurile ![]() si
si ![]() fiecare dintre cuplurile componente avand momentul
fiecare dintre cuplurile componente avand momentul ![]() cuplul rezultant are
momentul
cuplul rezultant are
momentul ![]()
d) Torsorul de reducere in punctul O este:
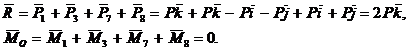
Trinomul invariant ![]() este nul. Sistemul este deci echivalent cu o forta unica situata pe axa centrala.
Deoarece
este nul. Sistemul este deci echivalent cu o forta unica situata pe axa centrala.
Deoarece ![]() axa centrala trece prin
punctul O si fiind paralela cu rezultanta, rezulta ca axa centrala este axa Oz. Sistemul de forte coplanare se poate
deci inlocui cu o
forta unica
axa centrala trece prin
punctul O si fiind paralela cu rezultanta, rezulta ca axa centrala este axa Oz. Sistemul de forte coplanare se poate
deci inlocui cu o
forta unica ![]() avand ca
suport axa Oz.
avand ca
suport axa Oz.
e) Torsorul de reducere in punctul O este:
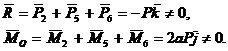
Trinomul invariant ![]() Sistemul de forte coplanare
Sistemul de forte coplanare ![]() este deci echivalent
cu o forta unica
este deci echivalent
cu o forta unica ![]() avand ca suport axa
centrala. Ecuatiile axei centrale vor
fi in acest
caz:
avand ca suport axa
centrala. Ecuatiile axei centrale vor
fi in acest
caz:
![]() si rezulta: x=2a; y=0.
si rezulta: x=2a; y=0.
f) Torsorul de reducere in punctul O este:
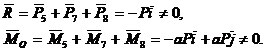
Trinomul invariant ![]() Axa centrala a sistemului va fi:
Axa centrala a sistemului va fi:
![]() adica dreapta de ecuatii y=0; z=-a, paralela cu axa Ox.
adica dreapta de ecuatii y=0; z=-a, paralela cu axa Ox.
Sistemul de forte ![]() este deci echivalent
cu o forta egala cu rezultanta
este deci echivalent
cu o forta egala cu rezultanta ![]() aplicata pe axa centrala si un cuplu de moment
aplicata pe axa centrala si un cuplu de moment ![]() colinear cu
rezultanta.
colinear cu
rezultanta.
Aplicatia 4
|
Fig: 48 |
O placa plana este formata din semicercul 1 de
raza R si dreptunghiul 2 cu
baza egala cu
diametrul semicercului, de inaltime h. (fig. 48). Care
trebuie sa fie
valoarea raportului ![]() pentru ca centrul
maselor intregii placi sa coincida cu centrul
semicercului O.
pentru ca centrul
maselor intregii placi sa coincida cu centrul
semicercului O.
Rezolvare:
Placa fiind simetrica fata de axa Oy, centrul maselor se afla pe aceasta axa, adica xC=0. Pentru ca centrul maselor sa se gaseasca in punctul O, va trebui ca yC=0, adica
(a) ![]()
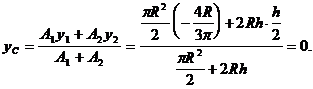
Din ecuatia de mai sus rezulta ca
(b) ![]()
Aplicatia 5
|
Fig: 49 |
O scandura patrata ABCD, de
greutate ![]() este atarnata de firul BE; cu varful A ea se sprijina pe un perete neted,
fix si vertical EA (fig. 49). Sa se determine reactiunea peretelui in punctul A, tensiunea T a firului si unghiul j, daca AB=BE=a..
este atarnata de firul BE; cu varful A ea se sprijina pe un perete neted,
fix si vertical EA (fig. 49). Sa se determine reactiunea peretelui in punctul A, tensiunea T a firului si unghiul j, daca AB=BE=a..
Rezolvare
Eliberand placa de legaturi si alegand sistemul de referinta ca in figura se obtin urmatoarele ecuatii scalare de echilibru:
(a) ![]()
(b) ![]()
(c) ![]()
de unde rezulta
(d) ![]()
iar tensiunea din fir si reactiunea normala a planului vor fi:
(e) ![]()
|
Fig: 50 |
Aplicatia 6
O bara simplu rezemata AB de lungime l si greutate neglijabila este actionata asa cum se arata in fig. 50. Dandu-se P, p, q, M, a, b, c sa se determine reactiunile din reazeme. Aplicatie numerica: P=98,1 KN, p=19,62 KN/m, q=15,6 KN/m, a=1m, b=1,5m, c=1,6m, l=4m, iar pentru momentul M se vor considera doua valori: M1=98,1 KNm si M2=294,3 KNm.
Rezolvare
Sarcina uniform distribuita p poate fi inlocuita cu forta P1=pa, aplicata in centrul fortelor paralele la distan paralele la distanta a/2 de reazemul A.
Sarcina liniar distribuita poate fi inlocuita cu forta rezultanta P2=(1/2)qb aplicata in centrul fortelor paralele la distanta (2/3)b de reazemul B.
Ecuatiile scalare de echilibru vor fi:
(a) ![]()
(b) ![]()
Rezolvand sistemul se obtine:
(c) 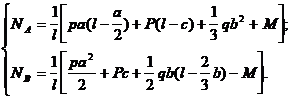
Efectuand inlocuirile numerice in primul caz gasim:
(d) NA=103,49 N ; NB=25,99 N
iar in al doilea:
(e) NA=152,54 N ; NB= -23,05 N
Cum NB< , conditia ca NB sa fie pozitiva nu este indeplinita si grinda se ridica de pe reazemul B ( in afara de cazul cand in B legatura este bilaterala
|
Fig: 51 |
Aplicatia 7
Pentru a initia miscarea de rotatie in jurul axei verticale (fig. 51), este necesar un cuplu de moment 750 Ncm. Sa se determine coeficientul de frecare de pivotare.
Rezolvare
Corpul de greutate G=750Nm este in stare de echilibru la limita. Sub actiunea cuplului M=750Ncm, miscarea de rotatie a acestui corp, in jurul axei verticale, este inerenta. Actiunea cuplului M este echilibrata de momentul de frecare de pivotare Mp. Avem asadar M= Mp. In cazul echilibrului la limita, momentul de frecare de pivotare fiind dat de relatia:
(a) ![]()
rezulta ca coeficientul de frecare de pivotare este egal cu:
(b) ![]()
Aplicatia 8
O franghie care cantareste 1 kg/m, se infasoara de 2,5 ori inprejurul unei bare
orizontale (fig 52). Ce lungime x de
franghie va
trebui lasata atarnand, daca are de sustinut o sarcina de 50 Kg ? Coeficientul de frecare dintre
franghie si bara este ![]()
|
Fig: 52a,b |
Rezolvare
Reprezentam actiunea portiunilor de franghie care atarna si a greutatii prin fortele ![]() si
si ![]() Pentru echilibru este
necesar ca intre marimile te
Pentru echilibru este
necesar ca intre marimile te
nsiunilor![]() si
si ![]() sa existe urmatorul raport:
sa existe urmatorul raport:
(a) 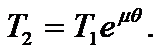
Tinand acum seama ca: T1=xgN, T2=2,5g+50g=52,5g N si unghiul de infasurare q p, obtinem:
(b) ![]()
de unde rezulta valoarea marimii cerute x
(c) 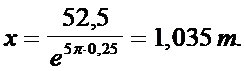
Aplicatia 9 (Roata trasa
Se considera roata trasa a unui vehicul (fig. 53). Se presupune ca tendinta de alunecare este in sens ascendent, iar tendinta de rostogolire in sens orar. Se cere sa se studieze echilibrul rotii.
Rezolvare
Reactiunile N, T si Mr au sensurile indicate in figura, iar conditiile de echilibru sunt
(a) 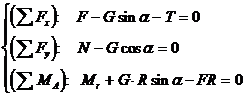
|
Fig: 53 |
La acestea se adauga si cele doua inecuatii ale frecarii:
(b) ![]()
Din primele trei relatii rezulta
(c) 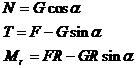
care introduse in inegalitatile (b), conduc la conditiile de echilibru:
(d) ![]()
sau inca explicitand in functie de F:
(e) 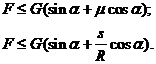
|
Fig: 54 |
De fapt numai una dintre aceste doua conditii este hotaratoare si anume cea mai mica. Astfel pentru:
![]() conditia a doua este hotaratoare si roata se va pune in miscare cand F
depaseste aceasta limita prin rostogolire,
conditia a doua este hotaratoare si roata se va pune in miscare cand F
depaseste aceasta limita prin rostogolire,
![]() prima conditie este hotaratoare si roata se va pune in miscare prin alunecare cand F depaseste aceasta limita
prima conditie este hotaratoare si roata se va pune in miscare prin alunecare cand F depaseste aceasta limita
Aplicatia 10 (Roata Motoare)
Se considera roata motoare a unui autovehicul actionata de greutatea G forta motoare F si cuplul motor de moment M (fig. 54). Se cere sa se studieze echilibrul rotii.
Rezolvare
Reactiunile N, T si Mr au sensurile indicate in figura, iar conditiile de echilibru sunt
(a) 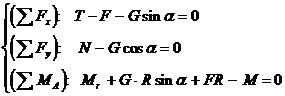
La acestea se adauga si cele doua inecuatii ale frecarii:
(b) ![]()
Din primele trei relatii rezulta
(c) 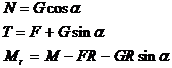
care introduse in inegalitatile (b), conduc la conditiile de echilibru:
(d) ![]()
sau inca explicitand prima inegalitate in functie de F si a doua in functie de M:
(e) 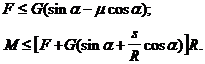
Din a doua inegalitate
rezulta valoarea ![]() minima necesara momentului cuplului
motor pentru ca sa fie
posibila miscarea. Din prima
inegalitate rezulta
minima necesara momentului cuplului
motor pentru ca sa fie
posibila miscarea. Din prima
inegalitate rezulta
(f) ![]()
care da valoarea minima a coeficientului de
frecare. Daca ![]() este mai mic decat aceasta valoare minima, tractiunea nu este posibila oricat de mare ar fi
valoarea cuplului motor. Astfel o locomotiva oricat de puternica ar fi nu poate
remorca un tren daca intre roti si sine coeficientul de
frecare
este mai mic decat aceasta valoare minima, tractiunea nu este posibila oricat de mare ar fi
valoarea cuplului motor. Astfel o locomotiva oricat de puternica ar fi nu poate
remorca un tren daca intre roti si sine coeficientul de
frecare ![]() este prea mic. Un fenomen analog are loc in timpul iernii in cazul unui automobil
cand rotile sale motoare aflandu-se in contact cu zapada inghetata, se invartesc pe loc fara ca automobilul sa se poata deplasa din cauza
coeficientului de frecare foarte mic.
este prea mic. Un fenomen analog are loc in timpul iernii in cazul unui automobil
cand rotile sale motoare aflandu-se in contact cu zapada inghetata, se invartesc pe loc fara ca automobilul sa se poata deplasa din cauza
coeficientului de frecare foarte mic.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








