| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Determinarea largimii benzii interzise a unui semiconductor - dispozitivul fizic experimental |
Determinarea largimii benzii interzise a unui semiconductor - dispozitivul fizic experimental
UNIVERSITATEA 'POLITEHNICA' DIN BUCURESTI
Consideratii teoretice
Mecanica cuantica arata ca microsistemele (electroni, molecule, ioni, etc.) izolate dispun de un spectru discret de energii, intre care pot efectua tranzitii. Tranzitiile spre nivelele energetice superioare au loc cu absorbtie de energie, din exterior, iar cele spre nivele inferioare, sunt insotite de emisie de radiatii .
Daca numarul atomilor creste foarte mult, interactiile suplimentare care apar duc la despicari ale nivelelor anterioare, rezultand un numar enorm de nivele, grupate sub forma unor manunchiuri numite benzi energetice permise. Acestea sunt separate in general de domenii lipsite de nivele energetice, numite benzi interzise.
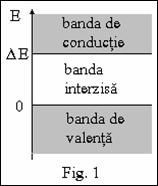
De o atentie aparte in cadrul studiului, se bucura doua benzi permise particulare, numite banda de valenta si banda de conductie (fig. 1). Ele sunt separate in mod obisnuit, de o banda interzisa de largime ∆E.
Banda de valenta reprezinta acel domeniu energetic, in care se incadreaza electronii ce participa la realizarea legaturilor intre atomi. Acestia sunt electroni legati in sensul ca se gasesc in vecinatatea unui atom, neavand o energie suficienta pentru a-l putea parasi. Daca primesc de undeva energia necesara, atunci ei pot deveni liberi sa circule peste tot si intra din punct de vedere energetic in banda de conductie. Se observa in fig. 1 ca surplusul energetic necesar trebuie sa fie ∆E.
Daca ∆E este mic, trecerea se face cu usurinta, iar substanta dispune de un fond important de electroni de conductie. Se spune ca acea substanta este un conductor electric.
Invers, daca ∆E ecte mare, trecerea se face greu, iar substanta este saraca in electroni de conductie. Ea conduce foarte prost curentul electric, practic de loc, de aceea se numeste izolator electric.
Intre aceste doua extreme se gasesc semiconductorii. Iata deci, ca largimea benzii interzise este o marime de interes fizic, important a fi cunoscuta pentru aplicatiile practice. Determinarea marimii ∆E in cazul unui semiconductor este de altfel si scopul acestei lucrari.
Principiul lucrarii
|
|
Tinand cont de cele expuse anterior, este usor de constatat ca rezistenta electrica a unui semiconductor trebuie sa scada odata cu cresterea temperaturii. In adevar, cresterea temperaturii inseamna un aflux energetic din exterior. Unii dintre electronii cantonati in banda de valenta, primesc energia necesara si devin liberi, trecand in banda de conductie. Ca atare, mai multi electroni de conductie inseamna o crestere a curentului electric, deci o rezistenta mai scazuta.
Teoria riguroasa a distributiei pe stari energetice a electronilor dintr-un solid este data de repartitia cuantica a lui Fermi - Dirac [1]. Pentru a evita calculele mai complicate corespunzand acestei repartitii cuantice, vom tine seama de faptul ca pentru semiconductori unele fenomenele de conductie pot fi aproximate corect de repartitia clasica canonica (Maxwell - Boltzmann). Aceasta prevede ca la echilibru, electronii sunt distribuiti dupa energiile pe care le au, astfel incat numarul dn(E) al celor care au energia cuprinsa in intervalul (E,E+dE), este dat de :
![]()
formula cunoscuta sub denumirea de 'distributie Boltzmann'.
In cazul nostru, considerand (vezi fig. 1) marginea superioara a benzii de valenta drept nivel de referinta (nivel de zero), numarul electronilor din banda de conductie va fi :
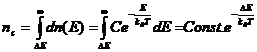
Cum rezistenta electrica este invers proportionala cu acest numar, avem ca :
![]()
Logaritmand aceasta ultima formula, obtinem :
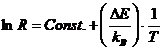
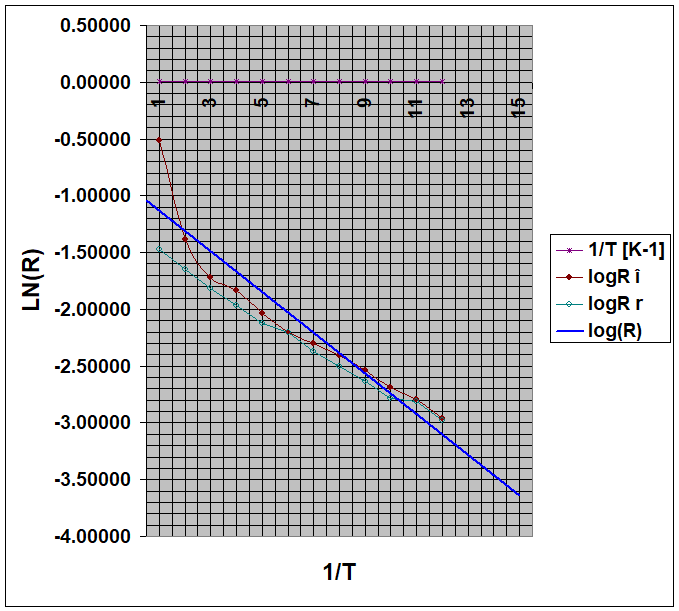
adica ecuatia unei drepte , in variabilele (lnR) si (1/T) cu panta p=(∆E)/kB. Astfel, daca dispunem de date experimentale asupra variatiei rezistentei semiconductorului cu temperatura, se poate trasa un grafic lnR=f(1/T) iar din panta acestuia se poate calcula largimea benzii interzise ∆E.
Dispozitivul experimental
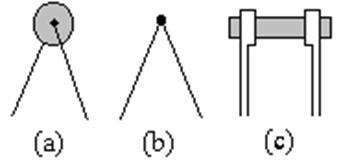
Semiconductorul folosit in lucrare este un termistor. Termistoarele sunt elemente semiconductoare de circuit, construite special in scopul utilizarii dependentei rezistentei lor electrice de temperatura. Ele se confectioneaza din amestecuri de oxizi metalici (de Cu, Fe, Cr, etc.) care sunt macinati si apoi presati impreuna cu un liant organic, iar ulterior sinterizati. De obicei se fac in forma de pastila (a), perla (b), sau bastonas (c). Termistoarele au dimensiuni mici, robustete, stabilitate a parametrilor si un pret de cost redus. Principalele utilizari practice ale acestora, sunt :
- masurarea sau reglarea temperaturii in locuri greu accesibile, de la distanta,
- compensarea variatiei cu temperatura a parametrilor altor dispozitive
- stabilizarea tensiunii.
|
|
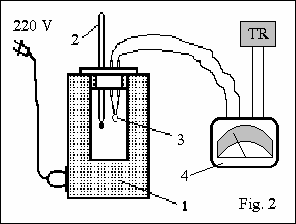
Dispozitivul experimental (fig. 2) cuprinde un cuptor electric (1) pentru incalzirea termisto-rului (3), un termometru (2) pentru masurarea temperaturii, un ohmmetru (4), care serveste la masurarea rezistentei termistorului si un transformator (TR) pentru alimentarea ohmmetrului. Cuptorul are inertie termica mare, astfel incat desi nu este alimentat printr-un reostat, ci direct de la retea, cresterea temperaturii este foarte lenta. Acest fapt inlatura necesitatea unui termostat, permitandune sa presupunem ca fiecare masurare de rezistenta se face in regim stationar.
Modul de lucru
|
|
Se porneste incalzirea cuptorului punandu-l la priza de 220V curent alternativ, apoi din 5 in 5 grade, se citeste valoarea rezistentei electrice a termistorului, avand grija ca citirea temperaturii sa se faca practic concomitent cu determinarea rezistentei. Temperatura finala nu trebuie sa depaseasca 100oC. Rezultatele masuratorilor se trec in tabelul 1. La terminarea masurarilor se scoate cuptorul din priza.
Prelucarea datelor experimentale.
Se completeaza datele din ultimele coloane ale tabelului si cu ajutorul lor se traseaza pe harie milimetrica graficul lnR=f(1/T). Se traseaza printre puncte o dreapta, iar din panta acesteia se calculeaza largimea benzii interzise ∆E.
Se
cunoaste valoarea constantei lui Boltzmann ![]()
|
t [oC] |
R[] i
|
R [] r |
T [K] |
1/T [K-1] |
logR i |
logR r |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||