
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Comunicatii
|
|
Qdidactic » stiinta & tehnica » comunicatii Prelucrarea datelor GPS |
Prelucrarea datelor GPS
Prelucrarea datelor GPS
1 Prelucrarea datelor
1.1 Gestionarea datelor
Incarcarea datelor Datele de observatie, ca si mesajul de navigatie si informatia aditionala, sunt in general stocate in format binar (dar depinde si de receptor).
Cei mai multi producatori de receptoare GPS ofera un sistem de gestiune a datelor pe care ei il recomanda a fi utilizat pentru prelucrarea datelor. Softul individual al sistemelor de prelucrare este insotit de manualele necesare si nu poate fi analizat in prezenta lucrare. In acest capitol este data o schema generala de prelucrare, care descrie principiile de baza.
Gestiunea datelor. Ca o regula, un receptor pe o singura frecventa, functionand cu o rata de esantionare de 1 secunda, colecteaza in timp de o ora un volum de date de 0.15 Mb. Prin urmare, de-a lungul a mai multe sesiuni GPS (in care se masoara cativa vectori de baza), poate fi colectionat un volum mare de date (de ordinul gigabyte). Rezulta ca arhivarea si procesarea acestor date intr-un timp rezonabil necesita adoptarea unei struturi de date potrivita. In continuare este prezentata una din variantele posibile, bazata pe principiul tabelarii statii/sesiuni.
Se presupun observatii GPS executate in 6 puncte, folosind 4 receptoare. Cu doua puncte de acoperire intre sesiuni, conform relatiei (7.4), sunt necesare doua sesiuni. Tabelul statii/sesiuni va avea aspectul prezentat in tabelul 1.
Tabelul 1. Tabelul statii/sesiuni
|
Statia |
Sesiunea a |
Sesiunea b |
|
P1 |
|
|
|
P2 |
|
|
|
P3 |
|
|
|
P4 |
|
|
|
P5 |
|
|
|
P6 |
|
|
Din acest tabel rezulta in timpul carei sesiuni a fost stationat un anumit punct sau invers, care puncte au fost incluse intr-o anumita sesiune. Ultima problema este mai relevanta, intrucat indica bazele ce pot fi calculate dintr-o anumita sesiune. Pentru acest motiv, este preferabila stocarea datelor pe sesiuni.
Headerul fiecarei sesiuni va contine identificatorul sesiunii si o lista punctelor stationate. Header-ul este urmat de blocurile de date. Primul bloc ar putea contine informatia referitoare la toti satelitii urmariti in timpul acelei sesiuni. Un bloc aditional ar putea fi rezervat pentru stocarea informatiilor aferente fiecarei statii:
- date masurate (faze, cod-distante, date meteo);
- rezultate imediate (solutia de navigatie, mesaje de diagnostic);
- informatii suplimentare (descrierea punctului, date despre receptor, componenta echipei de lucru)
Pentru exemplul considerat, organizarea fisierului este data in figura 1. Acest tip de stocare este numit lista liniara, datele fiind adresate prin folosirea pointerilor. Regasirea informatiilor pentru un anumit punct se face prin intermediul headerului, folosind identificatorul statiei.
Conversia datelor. Datele sunt receptionate in format binar si pot fi convertite in format ASCII, independent de calculator. In etapa de incarcare, datele sunt inca dependente de receptor, deci gestionarea lor descrisa anterior se poate face numai daca in fiecare sesiune au fost utilizate receptoare de acelasi tip. De asemenea, fiecare pachet de programe de prelucrare a observatiilor GPS foloseste propriul sau format, in care trebuie convertite in prealabil toate datele. Pentru a putea fi folosite diverse programe, datele trebuie convertite intr-un format independent de receptor.
|
|
Sesiunea: a |
|
|
Statia: P1 |
|
Header |
P2 |
|
|
P5 |
|
|
P6 |
|
|
Date despre sateliti |
|
|
Date in statia P1 |
|
Blocuri de date |
Date in statia P2 |
|
|
Date in statia P5 |
|
|
Date in statia P6 |
Figura 1. Gestionarea datelor printr-o lista liniara
Un astfel de format trebuie sa foloseasca definitii standard si sa fie destul de flexibil pentru diverse necesitati ulterioare. Au fost propuse mai multe formate dar numai cateva au capatat o raspandire acceptabila, cel mai important fiind RINEX (Receiver INdependent EXchange). Continutul formatului RINEX este prezentat in tabelul 2.
Acest format a fost definit in anul 1989 (o a doua versiune aparand in 1990) si contine trei tipuri de fisiere ASCII:
(1) fisierul cu datele de observatie;
(2) fisierul cu datele meteo;
(3) fisierul cu mesajul de navigatie.
Inregistrarile fisierelor au lungimi variabile, cu maximum 80 caractere pe linie. Fiecare fisier este compus din doua sectiuni (header si date). Sectiunea 'header' contine informatii generale iar sectiunea 'date' - datele de observatie. Fisierul cu mesajul de navigatie este creat pentru o anumita statie pe cand fisierul cu datele de observatie si fisierul cu datele meteo, trebuie sa fie creat pentru fiecare statie din fiecare sesiune.
Tabelul 2. Continutul formatului RINEX
|
Fisierul cu datele de observatie |
|
Fisierul cu datele meteorologice |
|
Fisierul cu mesajul de navigatie |
|
Header |
|
Header |
|
Header |
|
Statia |
|
Statia |
|
Comentarii |
|
Componenta echipei |
|
Tipul observatiilor |
|
|
|
Echipament |
|
Comentarii |
|
|
|
Excentricitati |
|
|
|
|
|
Tipul observatiilor |
|
|
|
|
|
Comentarii |
|
|
|
|
|
Date |
|
Date |
|
Date |
|
Epoca |
|
Epoca |
|
Epoca |
|
Sateliti |
|
Masuratori |
|
Parametri de corectie (ceas sateliti) |
|
Masuratori |
|
|
|
Parametri de corectie pentru orbita |
|
Flaguri |
|
|
|
Corectia ionosferica |
|
|
|
|
|
Flaguri |
Formatul RINEX a fost elaborat sub coordonarea U.S. National Geodetic Survey si a fost destul de repede utilizat de producatorii de receptoare si soft pentru conversia datelor dependente de receptor.
RINEX utilizeaza fisierul numit conventional 'ssssdddf.yyt', unde:
- ssss identificatorul statiei;
- ddd ziua din an;
- f numarul sesiunii;
- yy ultimele doua cifre ale anului curent;
- t tipul de fisier.
Identificarea satelitilor se face prin notatia conventionala 'snn', in care:
- s identificator al sistemului de sateliti;
- nn numarul satelitului (de exemplu numarul PRN)
Formatul RINEX permite stocarea observatiilor combinate (de exemplu GPS si TRANZIT.
1.2 Detectia si eliminarea alunecarilor de cicli
Definirea alunecarilor de cicli Cand un receptor este pornit, este masurata fractiunea bataii fazei (diferenta dintre purtatoarea receptionata de la satelit si semnalul de referinta generat de receptor) si este initializat un contor (numarator intreg). In timpul urmaririi, contorul este incrementat cu 1 de ficare data cand fractiunea de faza masurata face salturi de la 2 la 0. Astfel, la o anumita epoca, valoarea cumulata este suma fazei fractionare si a numarului intreg n (indicatia contorului). Numarul intreg initial N al ciclilor intre satelit si receptor este necunoscut si se numeste ambiguitate intreaga sau necunoscuta intreaga sau ambiguitate de cicli. Necunoscuta intreaga N ramane constanta atat timp cat legatura satelit-receptor nu se intrerupe. O eventuala pierdere a legaturii provoaca o reinitializare a contorului, fapt ce cauzeaza un salt al fazei momentane cumulata cu un numar intreg de cicli. Acest salt este numit alunecare de cicli si desigur afecteaza numai masuratorile de faza.
Reprezentarea grafica a unei alunecari de cicli este data in figura 2. Cand fazele masurate sunt reprezentate in functie de timp, trebuie sa se obtina o curba neteda. In cazul unei alunecari de cicli, pe curba apar salturi aparent inexplicabile.
Exista trei cauze care pot conduce la aparitia alunecarilor de cicli:
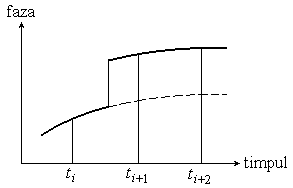
Figura 2. Reprezentarea grafica a alunecarilor de cicli
intreruperea temporara a legaturii cu satelitul din cauza obstacolelor (copaci, cladiri, poduri, forme de relief inalte etc.);
raport mic semnal/zgomot datorita conditiilor ionosferice nefavorabile, efectului multicai, dinamicii inalte a receptorului sau elevatiei prea mici a satelitului;
greseli ale softului receptorului, care conduc la procesare incorecta a semnalului.
Alunecarile de cicli pot fi cauzate si de oscilatoarele multifunctionale ale satelitului dar aceste situatii sunt rare.
Detectia alunecarilor de cicli presupune localizarea salturilor iar eliminarea lor consta in corectarea tuturor observatiilor de faza ulterioare pentru acel satelit si pentru acea purtatoare, cu o cantitate fixa. Detectia trebuie urmata de o evaluare cantitativa; in exemplul dat, aceasta ar putea consta intr-o masurare bruta a fazei. Determinarea marimii alunecarii si a corectiei de faza a datelor este adesea numita 'fixare' a alunecarii de cicli.
Marimi analizate Marimile supuse analizei sunt masuratorile fazei purtatoarei si cod-distantei. Pentru o singura statie, sunt analizate fazele, combinatiile de faze sau combinatiile de faze si cod-pseudodistante. Testele efectuate intr-un singur punct sunt importante deoarece permit detectia si corectarea alunecarilor de cicli cu ajutorul softului intern al receptorului. Cand sunt implicate doua statii (determinari relative), evaluarea cantitativa se face prin analiza diferentelor simple, duble si triple (vezi 8.2.1).
Marimile analizate in vederea evaluarii cantitative a alunecarilor de cicli sunt prezentate schematic in tabelul 3.
Faza
masurata ![]() poate fi modelata cu
relatia
poate fi modelata cu
relatia
Tabelul 3. Marimi analizate pentru detectarea alunecarilor de cicli
|
Date masurate |
Cantitati analizate |
|
Faza, pe frecventa simpla (L1 sau L2) |
Diferente simple Faza bruta Diferente duble Diferente triple |
|
Faza, pe frecventa duala (L1 si L2) |
Combinatia fazelor (reziduu ionosferic) |
|
Faza, pe frecventa simpla (L1 sau L2) si cod-distanta |
Combinatia faza/cod-distanta |
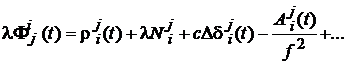 , (1)
, (1)
unde i,j desemneaza statia respectiv satelitul.
Termenul ![]() poate fi substituit cu
40,3 TEC/cos z' , conform (6.59). Este de remarcat ca ecuatia (1) contine in
membrul drept unii termeni dependenti de timp, care pot impiedica detectia
alunecarilor de cicli.
poate fi substituit cu
40,3 TEC/cos z' , conform (6.59). Este de remarcat ca ecuatia (1) contine in
membrul drept unii termeni dependenti de timp, care pot impiedica detectia
alunecarilor de cicli.
Modelul pentru combinatia fazei din frecventa duala este obtinut considerand o singura statie si un singur satelit. In acest caz, in (1), indicii inferiori si superiori pot fi omisi iar dependenta de frecventele L1 si L2 va fi aratata cu indicii inferiori respectivi:
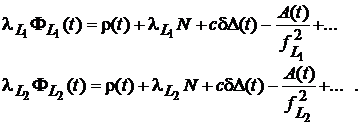 (2)
(2)
Scazand aceste doua ecuatii se obtine relatia
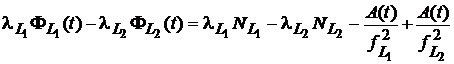 , (3)
, (3)
in care termenii idependenti de frecventa (distanta
geometrica si eroarea de ceas) dispar. Impartind prin ![]() rezulta
rezulta
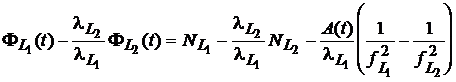 , (4)
, (4)
care poate fi transformata folosind c=f , din care se obtine imediat
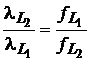 . (5)
. (5)
Avem deci
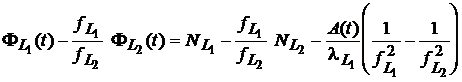 (6)
(6)
sau
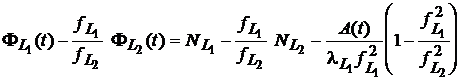 , (7)
, (7)
care este forma finala a combinatiei de frecvente duale.
Acest model este cunoscut si sub numele de 'reziduu ionosferic'.
Membrul drept al ecuatiei (7) arata ca reziduul ionosferic nu contine timpul ca
element de variatie a termenilor, exceptand refractia ionosferica. In
comparatie cu influenta asupra fazei brute prezentata in (1), efectul
ionosferei asupra combinatiei de frecventa duala este redus prin inmultire cu
factorul ![]() . Substituind valorile aproximative pentru
. Substituind valorile aproximative pentru ![]() si
si ![]() se obtine valoarea
procentuala a reducerii (circa 65%).
se obtine valoarea
procentuala a reducerii (circa 65%).
Daca nu sunt alunecari de cicli, variatiile temporale ale reziduului ionosferic trebuie sa fie mici pentru conditii ionosferice normale si pentru baze scurte. Ca indicatori ai alunecarilor de cicli sunt folosite salturile neasteptate ale valorilor succesive ale reziduului ionosferic. Ramane ca in continuare sa se stabileasca daca alunecarea s-a produs pe L1, pe L2 sau pe amandoua.
Remarcam ca reziduul ionosferic
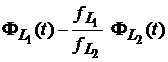
este o diferenta scalata a fazelor pe frecvente duale, ca si combinatia liniara care elimina refractia ionosferica, data de relatia (6.79):
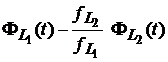 .
.
Aceste doua expresii difera esential prin natura
reciproca a coeficientilor lui ![]() .
.
O alta analiza cantitativa poate fi efectuata asupra combinatiei faza/cod-distanta. Modeland faza purtatoarei si cod-pseudodistanta cu relatiile
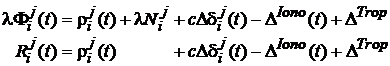 (8)
(8)
si efectuand diferenta
![]() , (9)
, (9)
se obtine o relatie in care, in partea dreapta, dispar termenii
dependenti de timp (exceptand refractia ionosferica). Influenta ionosferica
poate fi modelata sau neglijata. Neglijarea termenului ionosferic este posibila
deoarece modificarea ![]() , intre epoci apropiate, este mica.
, intre epoci apropiate, este mica.
Relatia (9) ofera posibilitatea unei analize cantitativa simpla dar are un neajuns important, rezultatul fiind influentat de nivelul zgomotului. Pentru seriile de timp ale combinatiilor faza/cod-distanta, nivelul zgomotului este in domeniul a 10 cicli. Acest nivel este datorat in principal nivelului de zgomot al masuratorilor de cod si in mai mica masura ionosferei. Zgomotul masuratorilor de cod este mai mare decat zgomotul masuratorilor de faza, deoarece rezolutia si efectele multicai sunt proportionale cu lungimea de unda. Primele tipuri de receptoare asigurau o rezolutie a masurarii de /100; hardul receptoarelor de astazi este capabil de masuratori cu rezolutia de aproximativ /1000. Se poate deduce imediat ca, la masurarea in cod P a unei cod-distante, nivelelul de zgomot este in limita a cativa centimetri. Combinatia faza/cod-distanta ofera deci o posibilitate ideala de analiza cantitativa pentru detectarea alunecarilor de cicli.
Pentru detectarea alunecarilor de cicli pe baza diferentelor simple, duble si triple se aplica un algoritm iterativ. In prima etapa, se calculeaza marimea aproximativa a vectorului bazei folosind combinatiile de faza necorectate de eventualele alunecari de cicli. Reziduurile obtinute sunt apoi analizate; pe baza concluziilor se reiau calculele, rezultand o solutie imbunatatita pentru vectorul bazei. De obicei sunt necesare cateva iteratii. Este de remarcat ca diferentele triple pot asigura convergenta si chiar o precizie ridicata fara fixarea alunecarilor de cicli.
Detectia si corectarea Modalitatile de analiza prezentate mai sus permit localizarea alunecarilor de cicli, prin inspectarea diferentei valorilor la doua epoci consecutive. Totodata, se obtine si o marime aproximativa a alunecarii (numarul de cicli). Pentru gasirea marimii corecte, sunt necesare investigatii asupra marimilor aferente unor serii de timp. Nu trebuie uitat ca in cazul fazelor, combinatiilor faza/cod-distanta, si diferentelor simple, duble, triple, valoarea detectata a alunecarii de cicli trebuie sa fie un intreg. Acest lucru nu este adevarat pentru reziduul ionosferic.
Una din metodele pentru detectarea alunecarilor de cicli este schema diferentelor. Principiul este foarte simplu si poate fi inteles pe baza unui exemplu. Presupunem y(ti), i=1,2,,7 ca serie de timp pentru un semnal ce contine un salt de cicli la epoca t4:
|
ti y(t) y1 y2 y3 y4 |
|
t1 0 0 t2 0 0 0 t3 0 t4 0 t5 0 0 0 t6 0 0 t7 |
In aceasta schema, y1,,y4 indica diferentele de ordinul unu,,patru efectuate. Daca datele nu sunt regulate, salturile sunt amplificate in diferentele de ordin superior si deci sunt usor de depistat. Din punct de vedere teoretic, acest lucru se justifica prin aceea ca diferentele sunt generate cu filtre substractive. Acestea sunt filtre trece-sus, care amortizeaza frecventele joase si elimina partea constanta. partea de inalta frecventa, cum ar fi salturile, sunt amplificate. Inlocuind semnalul y(t) spre exemplu cu faza si presupunand ca este o alunecare de cicli, efectul aplicarii schemei diferentelor devine evident. Oricare din cantitatile prezentate in tabelul 3 poate fi folosita ca semnal y(t).
O metoda de determinare a marimii alunecarii de cicli (saltului) este a potrivi cate o curba prin cantitatile testate, inainte si dupa producerea alunecarii. Marimea saltului este gasita prin determinarea deplasarii intre cele doua curbe. Potrivirea poate fi obtinuta printr-o regresie liniara simpla sau aplicand una din tehnicile de interpolare. Alte posibilitati sunt oferite de metodele de predictie, cum ar fi filtrarea Kalman. La o anumita epoca, valoarea functiei (una din cantitatile testate) pentru epoca urmatoare este evaluata (prezisa) ca informatie obtinuta din valorile precedente ale functiei. Valoarea prezisa este apoi comparata cu valoarea observata, diferentele punand in evidenta discontinuitatile (in cazul nostru alunecarile de cicli). Mai multe detalii asupra filtrarii Kalman sunt prezentate in capitolul 2.2.
Dupa ce o alunecare de cicli a fost detectata (prin una din metodele prezentate anterior), marimile care au servit la determinarea ei pot fi corectate prin adunarea valorii alunecarii (saltului) la fiecare din elementele secventei.
Trebuie
avut in vedere faptul ca daca determinarea s-a facut din combinatii ale
fazelor, aplicarea acestei valori asupra fazelor brute este ambigua. Singura
exceptie o constituie reziduul ionosferic, care permite o separare unica.
Consideram ecuatia (7) si notam cu ![]() respectiv
respectiv![]() modificarile ambiguitatilor intregi, generate de alunecarile
de cicli. Analiza efectuata asupra reziduului ionosferic permite determinarea
valorii N a saltului:
modificarile ambiguitatilor intregi, generate de alunecarile
de cicli. Analiza efectuata asupra reziduului ionosferic permite determinarea
valorii N a saltului:
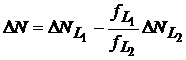 . (10)
. (10)
Cantitatea N
nu este un intreg. Relatia (10) reprezinta o ecuatie diofantica prin doi
intregi necunoscuti: ![]() ,
, ![]() . Rezolvarea acestei ecuatii cu doua necunoscute nu permite
obtinerea unei solutii unice. Acest lucru se vede imediat, punand conditia ca
N sa fie zero:
. Rezolvarea acestei ecuatii cu doua necunoscute nu permite
obtinerea unei solutii unice. Acest lucru se vede imediat, punand conditia ca
N sa fie zero:
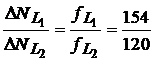 . (11)
. (11)
Egaland primul si ultimul raport si efectuand simplificarea obtinem forma generala a solutiei:
![]() . (12)
. (12)
Se observa ca perechile de valori (77;60), (154;120),
satisfac in egala masura ecuatia. Totusi, solutia este neambigua daca ![]() este mai mic de 77 cicli. Consideratiile de mai sus sunt pur
teoretice, deoarece masuratorile au fost presupuse ca neafectate de erori.
Pentru scopuri practice, este necesar sa se tina cont de zgomot. Un model
simplu al zgomotului pentru masuratorile de faza este:
este mai mic de 77 cicli. Consideratiile de mai sus sunt pur
teoretice, deoarece masuratorile au fost presupuse ca neafectate de erori.
Pentru scopuri practice, este necesar sa se tina cont de zgomot. Un model
simplu al zgomotului pentru masuratorile de faza este:
![]() , (13)
, (13)
care corespunde unei rezolutii de /100. Daca acelasi model este aplicat la ambele purtatoare (L1 si L2), se elimina zgomotul dependent de frecventa si efectul multicai. Acest lucru nu este insa valabil la receptoarele fara cod deoarece aici apare un zgomot aditional, introdus prin ridicarea la patrat.
In principiu, valoarea N este obtinuta din doua reziduuri ionosferice consecutive:
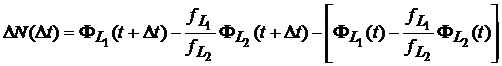 . (14)
. (14)
Aplicand aceastei ecuatii legea propagarii erorilor, obtinem:
![]() . (15)
. (15)
Pentru eroarea 3 se obtine valoarea aproximativa 0.07 cicli, care poate fi considerata ca rezolutia lui
N. Concluzia este ca dou
valori N calculate cu (10) pe
baza intregilor arbitrari ![]() si
si ![]() trebuie sa difere cu
cel putin 0.07 cicli pentru a putea fi unic separabile. O investigatie
sistematica a celor mai mici valori pentru
trebuie sa difere cu
cel putin 0.07 cicli pentru a putea fi unic separabile. O investigatie
sistematica a celor mai mici valori pentru ![]() ,
, ![]() este data in tabelul (4).
Marimilor
este data in tabelul (4).
Marimilor ![]() ,
, ![]() le-au fost atribuite,
prin permutari, valorile 0, 1, 2, , 5 iar N
a fost calculat cu (10). Ordonarea s-a facut dupa valorile N inscrise in prima coloana. Coloana a
doua contine diferentele celor doua functii consecutive. Pentru scurtarea
lungimii tabelului, au fost retinute numai valorile negative ale functiei
N.
le-au fost atribuite,
prin permutari, valorile 0, 1, 2, , 5 iar N
a fost calculat cu (10). Ordonarea s-a facut dupa valorile N inscrise in prima coloana. Coloana a
doua contine diferentele celor doua functii consecutive. Pentru scurtarea
lungimii tabelului, au fost retinute numai valorile negative ale functiei
N.
In
tabelul 4, randurile hasurate nu satisfac criteriul a cel putin 0.07 cicli diferenta. Pentru aceste valori, o
separatie neambigua nu este posibila deoarece zgomotul masuratorilor este mai
mare decat valorile de separat. Modul de alegere a combinatiei ![]() ,
, ![]() care trebuie
considerata vinovata de obtinerea unei diferente prea mica este destul de
intuitiv. Se observa ca, in toate cele patru cazuri, apar valori de +5 sau -5
pentru
care trebuie
considerata vinovata de obtinerea unei diferente prea mica este destul de
intuitiv. Se observa ca, in toate cele patru cazuri, apar valori de +5 sau -5
pentru ![]() sau
sau ![]() . Rezulta ca salturile de pana la 4 cicli pot fi
unic separate deoarece diferentele valorilor consecutive ale N sunt de cel putin 0.12 cicli (mai mari decat zgomotul, care
atinge valoarea de 0.07 cicli).
. Rezulta ca salturile de pana la 4 cicli pot fi
unic separate deoarece diferentele valorilor consecutive ale N sunt de cel putin 0.12 cicli (mai mari decat zgomotul, care
atinge valoarea de 0.07 cicli).
Concluziile ce se pot trage din analiza metodei de determinare a marimii alunecarilor de cicli pe baza combinarii datelor de observatie pe frecventa duala sunt urmatoarele:
datorita faptului ca masuratorile de faza sunt afectate de un zgomot presupus a avea valoarea data de (13), determinarea neambigua a salturilor este posibila numai pana la valori ale acestora mai mici de 4 cicli;
cu masuratorilor afectate de un zgomot mai mic, acest interval de separabilitate se extinde;
existenta unor salturi mari impune folosirea unei alte metode; combinatia masuratorilor de faza cu cele de cod-distante poate fi aplicata in asemenea situatii, dar si in acest caz pot sa apara greseli cand zgomotul cod-distantelor depaseste valoarea de 4 cicli.
Tabelul 4. N rezultat prin
permutari ale ![]() si
si ![]()
|
N Dif. |
|
N Dif. |
|
-11.42 -5 5 |
|
-3.72 -5 -1 |
|
-10.42 1.00 -4 5 |
|
-3.56 0.16 -1 2 |
|
-10.13 0.29 -5 4 |
|
-3.42 0.14 3 5 |
|
-42 0.71 -3 5 |
|
-3.28 0.14 -2 1 |
|
-13 0.29 -4 4 |
|
-3.13 0.15 2 4 |
|
-8.85 0.28 -5 3 |
|
-3.00 0.13 -3 0 |
|
-8.42 0.43 -2 5 |
|
-2.85 0.15 1 3 |
|
-8.13 0.29 -3 4 |
|
-2.72 0.13 -4 -1 |
|
-7.85 0.28 -4 3 |
|
-2.56 0.16 0 2 |
|
-7.56 0.29 -5 2 |
|
-2.44 0.12 -5 -2 |
|
-7.42 0.14 -1 5 |
|
-2.42 0.02 4 5 |
|
-7.13 0.29 -2 4 |
|
-2.28 0.14 -1 1 |
|
-6.85 0.28 -3 3 |
|
-2.13 0.15 3 4 |
|
-6.56 0.29 -4 2 |
|
-2.00 0.13 -2 0 |
|
-6.42 0.14 0 5 |
|
-1.85 0.15 2 3 |
|
-6.28 0.14 -5 1 |
|
-1.52 0.13 -3 -1 |
|
-6.13 0.15 -1 4 |
|
-1.56 0.16 1 2 |
|
-5.85 0.28 -2 -3 |
|
-1.44 0.12 -4 -2 |
|
-5.56 0.29 -3 2 |
|
-1.42 0.02 5 5 |
|
-5.42 0.14 1 5 |
|
-1.28 0.14 0 1 |
|
-5.28 0.14 -4 1 |
|
-1.15 0.13 -5 -3 |
|
-5.13 0.15 0 4 |
|
-1.13 0.02 4 4 |
|
-5.00 0.13 -5 0 |
|
-1.00 0.13 -1 0 |
|
-4.85 0.15 -1 3 |
|
-0.85 0.15 3 3 |
|
-4.56 0.29 -2 2 |
|
-0.72 0.13 -2 -1 |
|
-4.42 0.14 2 5 |
|
-0.56 0.16 2 2 |
|
-4.28 0.14 -3 1 |
|
-0.44 0.12 -3 -2 |
|
-4.13 0.15 1 4 |
|
-0.28 0.16 1 1 |
|
-4.00 0.13 -4 0 |
|
-0.15 0.13 -4 -3 |
|
-3.85 0.15 0 3 |
|
-0.13 0.02 5 4 |
|
-3.72 0.13 -5 -1 |
|
0.00 0.13 0 0 |
Uneori este posibil sa existe mai multe alunecari de cicli. In aceste cazuri, fiecare alunecare de cicli trebuie detectata si corectata, in mod separat. Dupa corectare, fazele si diferentele simple, duble si triple sunt utilizate la calculul vectorilor bazelor.
1.3. Determinarea ambiguitatii
Ambiguitatea si masuratorile de faza depind direct atat de receptor cat si de satelit. Ambiguitatea nu este dependenta de timp pe parcursul urmaririi neintrerupte a unui satelit. In modelul matematic pentru faza,
![]() , (16)
, (16)
ambiguitatea este notata cu N. Procesul de determinare a ambiguitatii, ca valoare intreaga, este numimit in mod obisnuit 'fixare'. Precizia ambiguitatii intregi este foarte importanta pentru determinarea vectorului bazei. S-au facut si unele experimente de determinare a vectorilor luand in calcul valori reale ale ambiguitatilor, uneori obtinandu-se diferente foarte mici (cativa milimetri) comparativ cu solutiile obtinute pe baza valorilor fixate.
In continuare vor fi demonstrate numai cateva principii de baza, utilizate de numeroase tehnici de determinare a ambiguitatii.
Determinarea ambiguitatilor cu faze masurate pe o singura frecventa
Cand sunt disponibile numai masuratori de faza pe o singura frecventa (fie L1 fie L2), masuratorile sunt modelate de ecuatia (16), care trebuie liniarizata. In functie de modelul de prelucrare ales, exista un anumit numar de necunoscute (coordonate, parametri de ceas etc.), care sunt estimate impreuna cu ambiguitatile N, printr-un proces de compensare. In mod evident, erorile nemodelate afecteaza parametrii estimati. De aceea, desi prin definitie ambiguitatile sunt intregi, valorile calculate vor fi reale. Dintre cauzele care genereaza acest fenomen, cele mai importante sunt: modelul incomplet al fazei, lungimea bazei (din cauza conditiilor atmosferice variabile) si erorile orbitale. Fixarea ambiguitatilor la valori intregi se face printr-un proces de compensare in trepte. Dupa o compensare initiala, ambiguitatea este rotunjita la intregul cel mai apropiat iar dintre ceilalti parametri se alege cel cu abaterea standard cea mai mica si se considera ca valoarea sa este de cea mai mare incredere. Acest parametru este considerat apoi cunoscut si se reia procesul de compensare (cu o necunoscuta mai putin), rezultand o alta valoare a ambiguitatii intregi. Procesul de calcul continua in acelasi mod, eliminand succesiv cate o necunoscuta. Cand se folosesc diferentele duble pentru baze scurte, aceasta metoda asigura de cele mai multe ori o buna determinare. Refractia ionosferica este singurul factor a carui modelare (obligatorie) poate impiedica determinarea corecta a tuturor ambiguitatilor.
Rezolvarea ambiguitatilor cu date de faza pe frecventa duala
Determinarea ambiguitatilor difera semnificativ in cazul datelor de faza pe frecventa duala. Frecventa duala ofera avantaje certe deoarece pot fi formate o varietate de combinatii liniare. Tehnicile de banda larga si banda ingusta au fost propuse inca din anul 197
Notand
cu ![]() ,
, ![]() datele de faza
masurate pe frecventele L1
respectiv L2, conform relatiei
(6.16), semnalul de banda larga este
datele de faza
masurate pe frecventele L1
respectiv L2, conform relatiei
(6.16), semnalul de banda larga este
![]() . (17)
. (17)
Frecventa acestui semnal este fl = 347.82 Mhz iar lungimea de unda corespondenta are valoarea l = 86.2 cm, semnificativ mai mare comparativ cu lungimile de unda originare (10 si 24.4 cm). Acest lucru permite o determinare mult mai usoara a ambiguitatilor intregi. Pentru prezentarea principiului, consideram modelele de fazelor pentru purtatoarele L1 si L2:
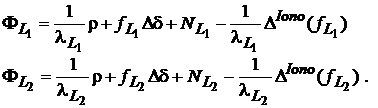 (18)
(18)
Inlocuind cu expresia sa in functie de frecventa (=c/f ) si termenul ionosferic cu Iono(f)=A/f 2 , relatiile (18) devin:
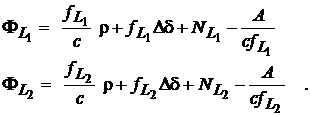 (19)
(19)
Diferenta acestor doua ecuatii da
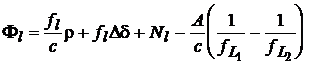 , (20)
, (20)
unde indicele inferior l precizeaza cantitatile de banda larga:
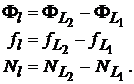
Compensarea
bazata pe modelele de banda larga da ambiguitatile de banda larga Nl , care sunt mult mai usor
determinate decat ambiguitatile purtatoarelor de baza. Pentru calcularea
ambiguitatilor fazelor masurate, luam ca exemplu purtatoarea L1. Impartim prima ecuatie (19)
la ![]() si ecuatia (20) la
si ecuatia (20) la![]() apoi le scadem. Se obtine relatia
apoi le scadem. Se obtine relatia
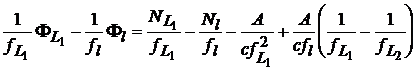 (21)
(21)
din care, dupa inmultire cu ![]() se poate explicita
ambiguitatea dorita:
se poate explicita
ambiguitatea dorita:
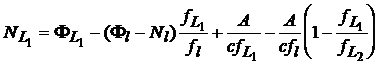 . (22)
. (22)
Termenii care reflecta influenta ionosferica pot fi scrisi sub forma
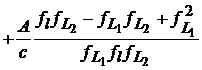 , (23)
, (23)
care este echivalenta cu
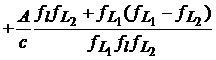 . (24)
. (24)
Termenul din paranteza poate fi inlocuit cu frecventa de banda larga, care apoi se simplifica, termenul ionosferic devenind
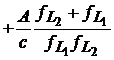 . (25)
. (25)
Revenind in (22), rezulta relatia de calcul a ![]() din ambiguitatea de
banda larga:
din ambiguitatea de
banda larga:
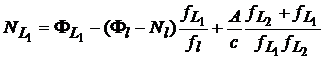 . (26)
. (26)
Inlocuind
in aceasta relatie L1 cu L2 si invers, se obtine
relatia de calcul pentru ![]() . Trebuie remarcat faptul ca distanta si corectia de
ceas nu mai apar. Termenul ionosferic ridica cele mai mari
semne de intrebare. Acest termen se va anula in cazul masuratorilor relative pe
baze scurte deoarece refractia ionosferica este aceeasi la ambele capete iar
calculele se executa folosind diferente de faza. Pentru baze lungi sau conditii
ionosferice neregulate, termenul ionosferic poate cauza probleme.
. Trebuie remarcat faptul ca distanta si corectia de
ceas nu mai apar. Termenul ionosferic ridica cele mai mari
semne de intrebare. Acest termen se va anula in cazul masuratorilor relative pe
baze scurte deoarece refractia ionosferica este aceeasi la ambele capete iar
calculele se executa folosind diferente de faza. Pentru baze lungi sau conditii
ionosferice neregulate, termenul ionosferic poate cauza probleme.
In afara
semnalului de banda larga, pot fi luate in considerare si alte combinatii
liniare ca de exemplu combinatia care elimina efectul ionosferic, ![]() . Dezavantajul acestei combinatii este ca ambiguitatea
corespondenta nu este un intreg. Se poate concluziona ca aplicarea oricareia
din cele doua metode prezinta un avantaj si un dezavantaj: fie ambiguitatea
poate fi determinata dar cu probleme generate de ionosfera, fie influenta
ionosferica este eliminata dar se distruge natura intreaga a ambiguitatii. S-a
propus folosirea altor combinatii liniare, intr-n domeniu destul de extins: de
la banda ingusta, cu lungimea de unda de 10.7 cm pana la banda foarte larga, cu
lungimea de unda de 172.4 cm.
. Dezavantajul acestei combinatii este ca ambiguitatea
corespondenta nu este un intreg. Se poate concluziona ca aplicarea oricareia
din cele doua metode prezinta un avantaj si un dezavantaj: fie ambiguitatea
poate fi determinata dar cu probleme generate de ionosfera, fie influenta
ionosferica este eliminata dar se distruge natura intreaga a ambiguitatii. S-a
propus folosirea altor combinatii liniare, intr-n domeniu destul de extins: de
la banda ingusta, cu lungimea de unda de 10.7 cm pana la banda foarte larga, cu
lungimea de unda de 172.4 cm.
Rezolvarea ambiguitatilor prin combinarea datelor de faza pe frecventa duala cu date de cod. La utilizarea tehnicilor de banda larga, termenul care provoaca cea mai mare incertitudine este refractia ionosferica, a carei valoare creste cu lungimea bazei. Acest neajuns poate fi eliminat prin combinarea datelor de faza cu cele de cod. Consideram modelele pentru fazele purtatoarelor si cod-distante pe frecventa duala, toate fiind exprimate in cicli:
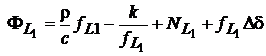 (27)
(27)
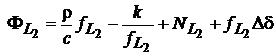 (28)
(28)
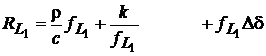 (29)
(29)
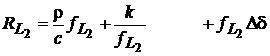 (30)
(30)
Termenul ionosferic a fost scris mai simplu, facandu-se
substitutia k=A/c. Avem la dispozitie
patru ecuatii cu patru necunoscute pentru fiecare epoca. Necunoscutele sunt
(/c +), k si ambiguitatile ![]() ,
, ![]() .
.
Calculul
ambiguitatilor se face prin intermediul ambiguitatii de scara larga ![]() , algoritmul de obtinere a relatiei de calcul fiind prezentat
in continuare.
, algoritmul de obtinere a relatiei de calcul fiind prezentat
in continuare.
Prin formarea diferentelor intre fazele purtatoarelor si cod-distante,
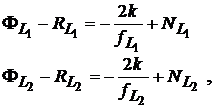 (31)
(31)
distanta geometrica si termenul de ceas sunt eliminate. Diferenta acestor doua ecuatii da
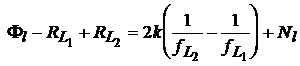 , (32)
, (32)
in care au fost introduse semnalul de banda larga ![]() si ambiguitatea de
banda larga Nl. Aducand la
acelasi numitor termenii din paranteza se obtine
si ambiguitatea de
banda larga Nl. Aducand la
acelasi numitor termenii din paranteza se obtine
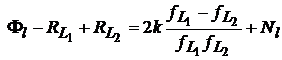 . (33)
. (33)
Termenul ionosferic k poate fi calculat prin impartirea ecuatiilor care dau
cod-distantele, (29) si (30), la ![]() respectiv
respectiv ![]()
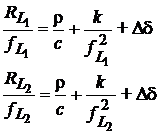 (34)
(34)
si scaderea celor doua relatii:
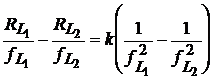 . (35)
. (35)
Aceasta poate fi scrisa sub forma
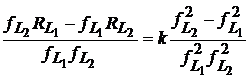 , (36)
, (36)
sau
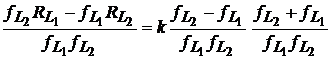 . (37)
. (37)
In final, dupa simplificare si impartire prin ![]() se obtine
se obtine
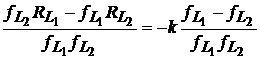 , (38)
, (38)
care poate fi substituita in (33) pentru eliminarea lui k. Acest lucru conduce la
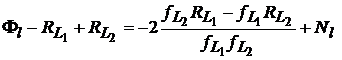 , (39)
, (39)
care poate fi rearanjata sub forma
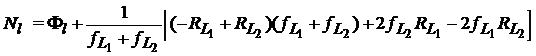 ,
,
(40)
sau
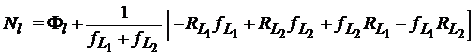 (41)
(41)
si in final
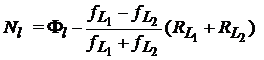 . (42)
. (42)
Aceasta ecuatie, destul de eleganta, permite determinarea ambiguitatii de scara larga Nl , pentru fiecare epoca si fiecare statie. Ecuatia este idependenta de lungimea bazei si de efectele ionosferice dar efetele multicai raman si afecteaza faza si codul, conform celor specificate la punctul 6.5. Efectele multicai sunt aproape exclusiv responsabile de variatia lui Nl cu cativa cicli de la o epoca la alta; problema poate fi rezolvata prin medierea aritmetica a valorilor pentru un anumit interval de timp.
Dispunand de ambiguitatile de banda larga, cu relatia (26) se pot obtine ambiguitatile unor faze oarecare, care sunt afectate de refractia ionosferica. Este insa posibila eliminarea efectului ionosferic, printr-o prelucrare matematica adecvata (prezentata in continuare).
Incepem din nou cu ecuatiile fazelor:
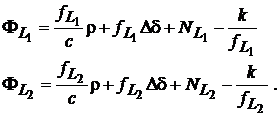 (43)
(43)
Inmultim prima ecuatie cu ![]() si pe a doua cu
si pe a doua cu ![]() . Prin scaderea relatiilor rezultate obtinem:
. Prin scaderea relatiilor rezultate obtinem:
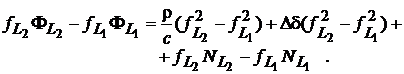 (44)
(44)
Introducand ambiguitatea de banda larga sub forma ![]() , aceasta relatie devine
, aceasta relatie devine
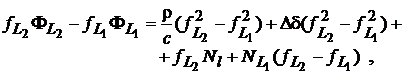 (45)
(45)
sau, tinand cont ca ![]() ,
,
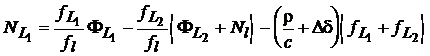 . (46)
. (46)
Aceasta ecuatie permite determinarea ambiguitatilor ![]() , neinfluentate de ionosfera. O remarca finala privind
formula de mai sus este ca aceasta este aproximativa deoarece combinarea unor
termeni continand Nl si
, neinfluentate de ionosfera. O remarca finala privind
formula de mai sus este ca aceasta este aproximativa deoarece combinarea unor
termeni continand Nl si ![]() (pentru eliminarea influentei ionosferei) distruge natura
intreaga a termenilor. Aceasta natura intreaga poate fi pastrata prin
calcularea separata a ambiguitatilor, mai intai Nl folosind (42) si apoi
(pentru eliminarea influentei ionosferei) distruge natura
intreaga a termenilor. Aceasta natura intreaga poate fi pastrata prin
calcularea separata a ambiguitatilor, mai intai Nl folosind (42) si apoi ![]() cu (46).
cu (46).
Modul de rezolvare descris mai sus nu este unic, putand fi folosite si alte proceduri pentru combinarea datelor din faza si cod. De asemenea, este de retinut ca aceasta tehnica ofera numai rezultate aproximative in aplicatiile cinematice (pentru determinarea instantanee a ambiguitatii). Daca exista cel putin o masuratoare suplimentara (cel putin cinci sateliti), atunci se poate aplica metoda celor mai mici patrate.
Atunci cand se compara diverse metode, un criteriu foarte important il constituie numarul de epoci necesare. Pentru o singura epoca, determinarea amiguitatilor este posibila daca (pentru baze scurte) sunt urmariti sapte sau mai multi sateliti; aceasta cerinta este cea mai restrictiva din toate cate apar la determinarile instantanee.
Tehnici de cautare
In tehnicile de cautare sunt folosite informatiile privind covarianta, rezultate din determinarea ambiguitatilor (reale) prin compensare. In interiorul unei regiuni care 'imbraca' valoarea reala a solutiei, toate valorile intregi sunt considerate drept candidate pentru ambiguitatea adevarata. Toate combinatiile posibile ale acestor ambiguitati sunt considerate ca valori cunoscute si sunt folosite in compensari separate. Se va obtine un set de solutii care, din punct de vedere al increderii, pot fi ordonate dupa valoarea crescatoare a erorii medii patratice. Prima dintre aceste solutii va fi considerata drept 'cea mai buna' si va fi considerata corecta daca raportul dintre erorile standard corespunzatoare ei si urmatoarei solutii este mai mare decat 2/3. Aceasta metoda poate fi utilizata numai pentru calculul unui singur vector de baza.
Intr-un paragraf anterior a fost mentionata o alta tehnica de cautare, numita fixarea secventiala (in trepte) a ambiguitatilor. Acesta metoda poatefi aplicata, dar necesita mult timp de efectuare a calculelor. O metoda putin mai sofisticata se bazeaza pe informatia statistica rezultata dintr-o compensare preliminara (a liniei de baza) si consta in:
estimarea ambiguitatilor si pozitiilor de determinat printr-o compensare standard;
folosirea informatiei statistice determinata prin compensare pentru fixarea ambiguitatilor la un anumit timp;
ambiguitatile determinate sunt folosite ca valori cunoscute si procedura este repetata;
toate ambiguitatile sunt valori intregi cunoscute si datele sunt recompensate, pentru obtinerea solutiei definitive.
O tehnica alternativa considera pozitia cunoscuta si determina ambiguitatile (necunoscute). Aceasta ar putea fi desfasurata in urmatorul mod:
se elimina ambiguitatile prin formarea diferentelor triple si se obtine o prima estimare a pozitiei (si a abaterii ei standard ), printr-o compensare;
centrat pe valoarea determinata, se construieste un cub de dimensiuni 888deexemplu 4 in fiecare directie si pentru fiecare coordonata), care se partitioneaza cu un grid regulat; acest cub contine matricea punctelor al caror punct central este chiar solutia obtinuta pe baza diferentelor triple;
fiecare din aceste puncte este considerat drept candidat pentru solutia corecta si in consecinta coordonatele ficaruia sunt inlocuite in ecuatia de observatii, procedand la noi compensari (de data aceasta se determina ambiguitatile);
din multimea de solutii pentru ambiguitati se alege drept corecta aceea pentru care 'inchiderea' pe valori intregi a fost cea mai buna;
cu valoarile ambiguitatilor astfel determinate se procedeaza la o noua prelucrare, cu diferentele simple, pentru calculul coordonatelor finale (care vor fi foarte apropiate de cele ale punctului din grid care a dat solutia cea mai buna pentru ambiguitati.
Figura 3. Tehnica de cautare
Metoda functiei de ambiguitate Principiul cubului gridat este folosit si pentru metoda functiei de ambiguitate. In expunerea metodei se pleaca de la modelul pentru diferentele simple,
![]() , (47)
, (47)
scris pentru punctele A si B si satelitul j, cu dimensiunea ciclului exprimata in radiani. Presupunand punctul A cunoscut, B va fi un candidat (unul din nodurile cubului gridat), deci primul termen din membrul drept este cunoscut si poate fi trecut in partea stanga a ecuatiei:
![]() . (48)
. (48)
Ambiguitatea ![]() poate fi reprezentata
circular. Un efect special rezulta daca termenul
poate fi reprezentata
circular. Un efect special rezulta daca termenul ![]() este
folosit ca argument al functiilor cosinus sau sinus, deoarece
este
folosit ca argument al functiilor cosinus sau sinus, deoarece ![]() este un intreg. Pentru
aceasta, intreaga expresie (48) este plasata in planul complex, prin
considerarea fiecarui membru ca putere la care se ridica
este un intreg. Pentru
aceasta, intreaga expresie (48) este plasata in planul complex, prin
considerarea fiecarui membru ca putere la care se ridica ![]() , unde
, unde ![]() :
:
![]() . (49)
. (49)
Aceasta relatie poate fi scrisa sub forma
![]() , (50)
, (50)
si este este reprezentata in planul complex in figura 4. Echivalenta
![]() (51)
(51)
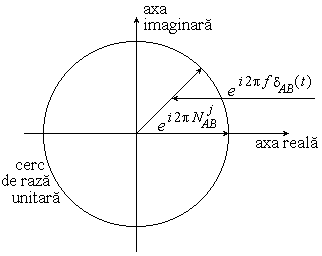
Figura 4 Reprezentarea vectorului in planul complex
permite reprezentarea unui vector unitar ale carui componente dupa axa reala si axa imaginara sunt cos() respectiv sin(). Pentru cazul nostru avem
![]() , (52)
, (52)
deoarece ![]() este un intreg.
Rezulta ca pentru o epoca si un satelit, din relatia (50) ramane
este un intreg.
Rezulta ca pentru o epoca si un satelit, din relatia (50) ramane
![]() . (53)
. (53)
Considerand nj sateliti, formarea sumei corespunzatoare epocii t conduce la
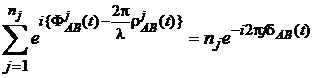 . (54)
. (54)
Daca se are in vedere existenta a mai mult decat o
singura epoca, trebuie tinut cont de faptul ca eroarea de ceas ![]() este variabila cu
timpul. Aceasta complicatie este rapid eliminata daca se tine cont de faptul ca
este variabila cu
timpul. Aceasta complicatie este rapid eliminata daca se tine cont de faptul ca
![]() este un vector unitar (vezi figura 4). Deoarece
este un vector unitar (vezi figura 4). Deoarece ![]() , din (54) se obtine
, din (54) se obtine
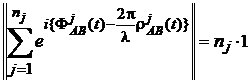 , (55)
, (55)
unde eroarea de ceas nu mai apare.
Pentru
exemplificare consideram patru sateliti si o situatie ideala, adica absenta
totala a erorilor (de masurare, de model si coordonate corecte pentru punctele A si B).
In acest caz, evaluarea partii stangi a ecuatiei (55) ar trebui sa produca
valoarea 4 (folosind diferentele simple ![]() obtinute din fazele
masurate si
obtinute din fazele
masurate si ![]() calculat din pozitiile
cunoscute ale statiei si satelitilor). Totusi, daca punctul B a fost ales incorect, rezultatul va fi
mai mic de 4. In situatii reale acest maximum nu poate fi niciodata realizat
din cauza erorilor de masurare si modelarii incomplete. Rezulta ca obiectivul
metodei il constituie obtinerea cu (55) a unui maxim, prin variatia
coordonatelor lui B.
calculat din pozitiile
cunoscute ale statiei si satelitilor). Totusi, daca punctul B a fost ales incorect, rezultatul va fi
mai mic de 4. In situatii reale acest maximum nu poate fi niciodata realizat
din cauza erorilor de masurare si modelarii incomplete. Rezulta ca obiectivul
metodei il constituie obtinerea cu (55) a unui maxim, prin variatia
coordonatelor lui B.
Daca ceasul receptorului este de inalta stabilitate, in interiorul unui interval de timp restrans, teoretic este posibil sa se includa mai mult decat o epoca de observatii astfel incat valoarea absoluta sa ramana aceeasi. Pentru nt epoci, contributia tuturor epocilor este data de relatia
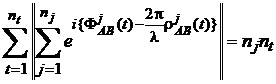 , (56)
, (56)
in care, pentru simplitate, s-a presupus observarea aceluiasi numar de sateliti la toate epocile. Membrul stang al acestei relatii este o functie de ambiguitate. Ca si pentru o singura epoca, trebuie gasit maximul functiei de ambiguitatet. In general, el va fi mai mic decat valoarea teoretica nt.nj.
Procedura de aplicare a metodei functiei de ambiguitate este simpla. Presupunem o solutie aproximativa pentru punctul B, obtinuta de exemplu cu diferente triple. Pe aceasta solutie se centreaza un cub partitionat cu ajutorul unui grid, fiecare punct nodal constituind un candidat pentru solutia finala. Se calculeaza valoarea functiei de ambiguitate (56) pentru toate diferentele simple. Punctul din grid care produce valoarea cea mai mare pentru functia de ambiguitate (care, teoretic, ar putea fi egala cu numarul total al diferentelor simple) este considerat drept solutia cea mai probabila. Cu aceasta solutie, ambiguitatile se calculeaza folosind diferentele duble. De asemenea, se poate efectua o prelucrare cu diferentele duble, pentru a avea o verificare a pozitiei lui B si a valorilor ambiguitatilor. In final, cu ambiguitatile fixate, se calculeaza coordonatele definitive ale punctului B.
Metoda
functiei de ambiguitate este complet insensibila la alunecarile de cicli. Acest
lucru se observa imediat in ecuatia (52), unde schimbarea ambiguitatii cu un
intreg arbitrar ![]() produce tot un intreg,
deci marimea
produce tot un intreg,
deci marimea ![]() ramane unitara. Prin
urmare si ecuatiile urmatoare raman neschimbate. Alte metode impun detectarea
si corectarea alunecarilor de cicli inaintea calcularii ambiguitatii.
ramane unitara. Prin
urmare si ecuatiile urmatoare raman neschimbate. Alte metode impun detectarea
si corectarea alunecarilor de cicli inaintea calcularii ambiguitatii.
Problema accelerarii procedurii este foarte importanta si a fost indelung studiata deoarece densitatea gridului influenteaza puternic volumul de calcule iar in unele situatii devine problematica gasirea corecta a valorii maxime (daca sunt mai multe maxime relative pentru functia de ambiguitate). Pentru ilustrare, presupunem un cub cu dimensiunile de 6m/6m/6m si un pas al gridului de 1 cm. Vor rezulta 6013 2.17.108 solutii posibile care trebuie sa fie verificate cu functia de ambiguitate (56).
2 Compensarea, filtrarea si potrivirea
2.1 Compensarea prin metoda celor mai mici patrate
Compensarea standard Pot fi utilizate numeroase tehnici de compensare dar aici se va prezenta numai metoda cea mai raspandita si anume compensarea prin metoda celor mai mici patrate cu parametri. Aceasta se bazeaza pe ecuatiile de observatie exprimate ca functii de parametrii necunoscuti. Deoarece uneori aceste functii nu sunt liniare, ele se liniarizeaza prin dezvoltari in serie Taylor, doua aspecte fiind de retinut relativ la acest lucru: 1) sunt necesare valori aproximative pentru parametri si 2) dezvoltarea in serie Taylor trebuie sa fie truncheata dupa al doilea termen, ca sa se obtina functii liniare de respectivele necunoscute. Modelul liniar al observatiilor rezultat poate fi reprezentat prin relatia matriceala
![]() , (57)
, (57)
unde

Introducand si notatiile
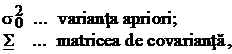
matricea cofactorilor observatiilor va fi
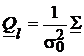 (58)
(58)
iar
![]() (59)
(59)
este matricea ponderilor. Considerand n observatii si u parametri necunoscuti, matricea coeficientilor ![]() va avea n randuri
si u coloane. Pentru n>u, sistemul (57) este supradeterminat si, in general,
inconsistent din cauza erorilor de masurare sau zgomotului. Pentru asigurarea
consistentei, la vectorul observatiilor este adunat vectorul zgomotului n si astfel ecuatia (57) se transforma
in
va avea n randuri
si u coloane. Pentru n>u, sistemul (57) este supradeterminat si, in general,
inconsistent din cauza erorilor de masurare sau zgomotului. Pentru asigurarea
consistentei, la vectorul observatiilor este adunat vectorul zgomotului n si astfel ecuatia (57) se transforma
in
![]() . (60)
. (60)
Numai una din solutiile acestui sistem satisface
principiul celor mai mici patrate (![]() ). Aplicarea acestui principiu asupra ecuatiilor
observatiilor (60) conduce la obtinerea sistemului ecuatiilor normale
). Aplicarea acestui principiu asupra ecuatiilor
observatiilor (60) conduce la obtinerea sistemului ecuatiilor normale
![]() , (61)
, (61)
a carui solutie
![]() (62)
(62)
poate fi scrisa mai simplu
![]() , (63)
, (63)
unde ![]() si
si ![]() .
.
Matricea
cofactorilor ![]() este obtinuta din
este obtinuta din ![]() , prin aplicarea legii propagarii covariantei:
, prin aplicarea legii propagarii covariantei:
![]() . (64)
. (64)
Prin efectuarea substitutiei ![]() , aceasta ecuatie se
reduce la
, aceasta ecuatie se
reduce la
![]() . (65)
. (65)
Compensarea secventiala (pe grupe). Consideram modelul (60) al observatiilor partitionat in doua subseturi:
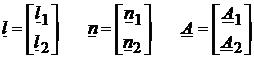 . (66)
. (66)
Folosind numai primul subset, in baza relatiilor (62) si
(65) poate fi calculata solutia preliminara ![]() cu:
cu:
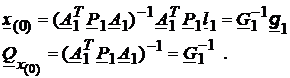 (67)
(67)
Presupunand ca nu exista corelatii intre cele doua subseturi de observatii, matricea ponderilor va fi o matrice bloc-diagonala:
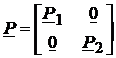 . (68)
. (68)
Matricea ![]() si vectorul
si vectorul ![]() pentru compensarea
intregului set de observatii se obtin prin adunarea matricilor respectiv
vectorilor corespunzatori celor doua subseturi:
pentru compensarea
intregului set de observatii se obtin prin adunarea matricilor respectiv
vectorilor corespunzatori celor doua subseturi:
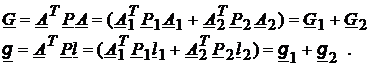 (69)
(69)
Daca modificarea solutiei preliminare ![]() datorita subsetului
aditional
datorita subsetului
aditional ![]() este notata cu
este notata cu ![]() , atunci
, atunci
![]() (70)
(70)
constituie noua formulare a compensarii. Aceasta ecuatie poate fi rearanjata sub forma
![]() , (71)
, (71)
unde membrul drept poate fi simplificat in baza primei
relatii (67), conform careia ![]() :
:
![]() . (72)
. (72)
Tinand cont ca, in baza relatiilor (69), ![]() si
si ![]() , obtinem
, obtinem
![]() , (73)
, (73)
sau
![]() , (74)
, (74)
de unde
![]() (75)
(75)
sau, in final
![]() (76)
(76)
unde s-a efectuat notatia
![]() . (77)
. (77)
Este de remarcat ca in (76) termenul ![]() poate fi considerat ca
valoare de asteptat pentru observatiile
poate fi considerat ca
valoare de asteptat pentru observatiile ![]() .
.
Obiectivul
urmator il constituie calculul corectiei ![]() ce trebuie adusa
matricii preliminare a cofactorilor
ce trebuie adusa
matricii preliminare a cofactorilor ![]() . Se porneste de la relatia
. Se porneste de la relatia
![]() , (78)
, (78)
in care ![]() este matricea unitate. Aceasta ecuatie poate fi scrisa si sub
forma
este matricea unitate. Aceasta ecuatie poate fi scrisa si sub
forma
![]() (79)
(79)
si, deoarece ![]() , se reduce la
, se reduce la
![]() (80)
(80)
sau
![]() (81)
(81)
si, facand substitutia ![]() , se obtine:
, se obtine:
![]() . (82)
. (82)
Comparand aceasta ecuatie cu (77), se mai poate introduce
si notatia ![]() , rezultand
, rezultand
![]() . (83)
. (83)
Matricea ![]() satisface relatia
satisface relatia
![]() , (84)
, (84)
bazata pe o formula dedusa de Bennet (1965). Aceasta
ecuatie poate fi aplicata la inversarea matricilor modificate de forma (![]() ) unde
) unde ![]() este cunoscuta a
priori. Ultima egalitate din (84) poate fi verificata prin inmultirea ambilor
membri, la stanga cu (
este cunoscuta a
priori. Ultima egalitate din (84) poate fi verificata prin inmultirea ambilor
membri, la stanga cu (![]() ) si la dreapta cu
) si la dreapta cu ![]() . Este foarte important de retinut din (84) ca determinarea
lui
. Este foarte important de retinut din (84) ca determinarea
lui ![]() pe baza primei
egalitati implica inversarea unei matrice de dimensiuni u
pe baza primei
egalitati implica inversarea unei matrice de dimensiuni u![]() u, u fiind numarul parametrilor
necunoscuti. Daca se foloseste cea de-a doua egalitate, atunci este necesara
inversarea unei matrice
u, u fiind numarul parametrilor
necunoscuti. Daca se foloseste cea de-a doua egalitate, atunci este necesara
inversarea unei matrice ![]() ,
, ![]() fiind numarul
observatiilor din al doilea subset. Deci, a doua modalitate de calcul este
recomandabila doar daca
fiind numarul
observatiilor din al doilea subset. Deci, a doua modalitate de calcul este
recomandabila doar daca ![]() < u.
< u.
Asupra
compensarii pe grupe este necesar sa facem o ultima precizare. Atat in
relatiile care dau ![]() - (76), (77) - cat si
in cele pentru calculul lui
- (76), (77) - cat si
in cele pentru calculul lui ![]() - (83), (77) - nu apar
explicit nici matricea
- (83), (77) - nu apar
explicit nici matricea ![]() nici vectorul
nici vectorul ![]() , aferente primului subset de observatii. Totusi, pot fi
facute substitutiile formale
, aferente primului subset de observatii. Totusi, pot fi
facute substitutiile formale ![]() si
si ![]() , modelul pentru compensatea secventiala putand fi formulat
ca
, modelul pentru compensatea secventiala putand fi formulat
ca
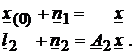 (85)
(85)
Acest model arata ca estimarile preliminare ![]() ale parametrilor
necunoscuti sunt introduse in compensarea secventiala ca observatii. Acest mod
de abordare este des utilizat, impreuna cu filtrarea Kalman.
ale parametrilor
necunoscuti sunt introduse in compensarea secventiala ca observatii. Acest mod
de abordare este des utilizat, impreuna cu filtrarea Kalman.
2.2 Filtrarea Kalman
Introducere. Consideram un sistem dinamic, de exemplu un vehicul in miscare. Parametrii necunoscuti (de exemplu coordonatele si viteza) fomeaza elementele vectorului starilor. Acest vector, dependent de timp, poate fi prezis pentru orice moment t, prin intermediul unui sistem de ecuatii. Valorile prezise pot fi imbunatatite pe baza observatiilor continand informatii despre oricare din componentele vectorului starilor.
Intregul proces este cunoscut sub numele de filtrarea Kalman si corespunde compensarii secventiale in cazul observatiilor statice. Prin urmare, se obtin estimarile optime ale necunoscutelor, pe baza observatiilor efectuate pana la epoca t. Totusi, nu este nevoie ca aceste date sa fie pastrate pentru epocile urmatoare.
Aspecte
preliminarii. Vectorul starilor (dependent
de timp) ![]() , alcatuit din parametrii necunoscuti ai sistemului dinamic,
poate fi modelat cu un sistem de ecuatii diferentiale de ordinul intai de forma
, alcatuit din parametrii necunoscuti ai sistemului dinamic,
poate fi modelat cu un sistem de ecuatii diferentiale de ordinul intai de forma
![]() , (86)
, (86)
unde
![]() derivata in raport cu timpul a vectorului
starilor;
derivata in raport cu timpul a vectorului
starilor;
![]() matricea dinamicilor;
matricea dinamicilor;
![]() zgomotul.
zgomotul.
La epoca initiala ![]() , vectorul starilor
, vectorul starilor ![]() si matricea cofactorilor
si matricea cofactorilor ![]() sunt presupuse a fi cunoscute. O solutie generala pentru
sistemul de ecuatii (86) exista numai daca matricea
sunt presupuse a fi cunoscute. O solutie generala pentru
sistemul de ecuatii (86) exista numai daca matricea ![]() are coeficienti
periodici sau constanti. In ultimul caz, aceasta solutie se poate scrie ca
are coeficienti
periodici sau constanti. In ultimul caz, aceasta solutie se poate scrie ca
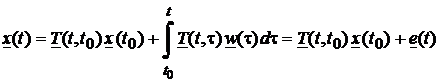 , (87)
, (87)
aici ![]() reprezentand matricea
de tranzitie. Aceasta matrice rezulta din dezvoltarea in serie Taylor a vectorului
de stare,
reprezentand matricea
de tranzitie. Aceasta matrice rezulta din dezvoltarea in serie Taylor a vectorului
de stare,
![]() , (88)
, (88)
care poate fi scrisa, substituind (86) si neglijand
zgomotul ![]() sub forma
sub forma
![]() , (89)
, (89)
sau, prin comparare cu (87),
![]() . (90)
. (90)
In acelasi fel, introducand notatia ![]() , matricea de tranzitie poate fi scrisa ca o serie
infinitafunctie de
, matricea de tranzitie poate fi scrisa ca o serie
infinitafunctie de ![]() :
:
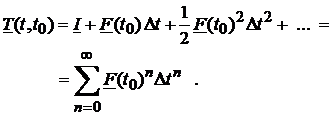 (91)
(91)
Matricea
cofactorilor ![]() a vectorului starilor
a vectorului starilor ![]() poate fi calculata
prin intermediul (87), folosind legea de propagare a covariantei:
poate fi calculata
prin intermediul (87), folosind legea de propagare a covariantei:
![]() (92)
(92)
Analizand relatiile (87) si (91) se poate trage concluzia
ca problema esentiala a filtrarii Kalman o reprezinta definirea matricii de
tranzitie ![]() si a matricii
cofactorilor
si a matricii
cofactorilor ![]() .
.
Punerea
problemei. Plecand de la o epoca
initiala ![]() , vectorul starilor
, vectorul starilor ![]() poate fi calculat
pentru orice epoca t, folosind
sistemul de ecuatii (87). Tinand cont de sistemul zgomotului
poate fi calculat
pentru orice epoca t, folosind
sistemul de ecuatii (87). Tinand cont de sistemul zgomotului ![]() , presupunem ca pentru epoca t sunt disponibile observatiile
, presupunem ca pentru epoca t sunt disponibile observatiile ![]() si matricea
corespunzatoare a cofactorilor
si matricea
corespunzatoare a cofactorilor ![]() . Aceste date pot fi raportate la la noul vector al
starilor
. Aceste date pot fi raportate la la noul vector al
starilor ![]() - obtinut eventual
dupa o liniarizare - dat de ecuatia
- obtinut eventual
dupa o liniarizare - dat de ecuatia
![]() . (93)
. (93)
Daca se considera vectorul starilor ![]() si vectorul
observatiilor
si vectorul
observatiilor ![]() ca niste cantitati
stochastice, atunci problema se reduce la o compensare secventiala:
ca niste cantitati
stochastice, atunci problema se reduce la o compensare secventiala:
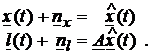 (94)
(94)
Acest sistem este echivalent cu (85). In aceasta situatie, solutiile rezulta imediat din (76) si 83), utilizand notatiile curente:
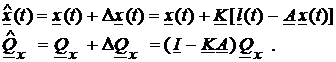 (95)
(95)
Matricea ![]() va fi, conform (84):
va fi, conform (84):
![]() . (96)
. (96)
Exemplu. Consideram un vehicul in miscare rectilinie, cu viteza
constanta v, a carui deplasare este
afectata de o acceleratie aleatoare a.
De asemenea, presupunem ca la epoca ![]() sunt cunoscute pozitia
(uni-dimensionala)
sunt cunoscute pozitia
(uni-dimensionala) ![]() cu varianta
cu varianta ![]() , viteza
, viteza ![]() cu varianta
cu varianta ![]() precum si varianta
zgomotului
precum si varianta
zgomotului ![]() . In plus, se presupune ca vehiculul este observata la epoca
. In plus, se presupune ca vehiculul este observata la epoca ![]() , observatia avand varianta
, observatia avand varianta ![]() . Vectorul starilor are drept componente pozitia si viteza
vehiculului. Deci, pentru epoca initiala avem:
. Vectorul starilor are drept componente pozitia si viteza
vehiculului. Deci, pentru epoca initiala avem:
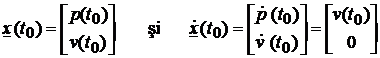 . (97)
. (97)
Inlocuind acesti vectori si acceleratia variabila a in (86), matricea dinamicii si
vectorul zgomot pentru epoca ![]() sunt:
sunt:
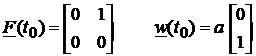 . (98)
. (98)
Din ecuatia (91), se obtine matricea de tranzitie
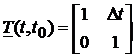 . (99)
. (99)
Presupunand ca in intervalul ![]() acceleratia este
constanta, cu (87) se obtine vectorul zgomot
acceleratia este
constanta, cu (87) se obtine vectorul zgomot
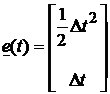 . (100)
. (100)
Este de remarcat faptul ca, datorita presupunerilor facute, elementele vectorului starilor prezise pot rezulta si din formula miscarii accelerate.
Matricea
cofactorilor ![]() corespunzatoare vectorului starilor prezise rezulta din
relatia (92):
corespunzatoare vectorului starilor prezise rezulta din
relatia (92):
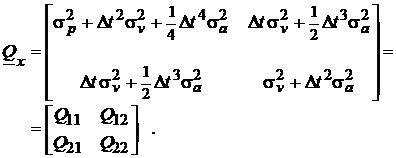 (101)
(101)
Deoarece ecuatia observatiei este ![]() , matricea
, matricea ![]() din relatia (94) se
reduce la un vector linie
din relatia (94) se
reduce la un vector linie
![]() , (102)
, (102)
iar matricea ![]() la un vector coloana
la un vector coloana
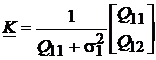 . (103)
. (103)
Acum, noul vector al starilor ![]() si matricea
corespunzatoare a cofactorilor
si matricea
corespunzatoare a cofactorilor ![]() pot fi calculate cu
relatiile (95).
pot fi calculate cu
relatiile (95).
2.3 Netezirea
Procesul de imbunatatire a estimarilor anterioare pentru vectorul starilor cu o noua masuratoare se numeste netezire. Spre deosebire de filtrarea Kalman in timp real, netezirea este o prelucrare ulterioara. In continuare va fi prezentata una din tehnicile de netezire posibil de aplicat. Folosind notatiile
![]() vectorul starilor prezise
vectorul starilor prezise
![]() vectorul starilor actualizate
vectorul starilor actualizate
![]() vectorul starilor netezite,
vectorul starilor netezite,
se poate deduce relatia pentru netezirea optima
![]() , (104)
, (104)
unde matricea castig este
![]() . (105)
. (105)
La epoca ultimelor masuratori, vectorul starilor actualizate este identic cu cel al starilor filtrate, deci poate fi lansat un algoritm invers. Din ecuatia (104) se poate concluziona ca procesul de netezire necesita cunoasterea vectorilor starilor prezise si actualizate, matricile cofactorilor la epocile actualizarilor precum si matricile de tramzitie intre actualizari. Fiind deci necesar un mare volum de date, destul de greu de obtinut si manevrat, metoda optima de netezire este deseori inlocuita cu metode empirice.
3 Compensari cu modelele matematice GPS
3.1 Liniarizarea
Analiand modelele de la capitolul 8, se observa ca singurul termen care contine necunoscute in forma neliniara este . In continuare se prezinta, in detaliu, modul de liniarizare a lui . Relatia
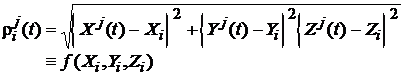 (106)
(106)
contine coordonatele necunoscute ale punctelor ![]() , in forma neliniara. Presupunand ca se cunosc valorile
aproximative
, in forma neliniara. Presupunand ca se cunosc valorile
aproximative ![]() ale necunoscutelor, atunci pot fi calculate distantele
aproximative
ale necunoscutelor, atunci pot fi calculate distantele
aproximative ![]() , cu relatia
, cu relatia
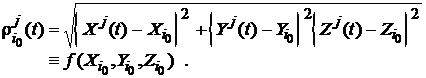 (107)
(107)
Dispunand de aceste valori, necunoscutele ![]() pot fi scrise ca
pot fi scrise ca
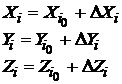 (108)
(108)
![]() fiind noile
necunoscute. In acest mod, necunoscutele initiale au fost divizate intr-o parte
cunoscuta (valorile aproximative
fiind noile
necunoscute. In acest mod, necunoscutele initiale au fost divizate intr-o parte
cunoscuta (valorile aproximative ![]() ) si o parte necunoscuta (corectiile
) si o parte necunoscuta (corectiile ![]() ). Aceasta divizare
prezinta marele avantaj ca functia
). Aceasta divizare
prezinta marele avantaj ca functia ![]() este posibil sa fie
inlocuita cu functia echivalenta
este posibil sa fie
inlocuita cu functia echivalenta ![]() , pe care o putem dezvolta in serie Taylor in jurul valorii
aproximative. Avem deci
, pe care o putem dezvolta in serie Taylor in jurul valorii
aproximative. Avem deci
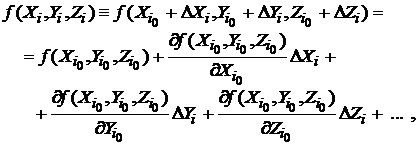 (109)
(109)
din dezvoltare fiind retinut numai termenii liniari;
altfel, necunoscutele ![]() vor apare din nou in
forma neliniara. Derivatele partiale sunt obtinute din (107)
vor apare din nou in
forma neliniara. Derivatele partiale sunt obtinute din (107)
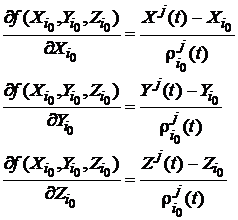 (110)
(110)
si reprezinta componentele versorului directiei din
satelit spre pozitia aproximativa a statiei. Inlocuind (107) si (110) in (109)
si tinad cont de echivalenta dintre ![]() si
si ![]() obtinem:
obtinem:
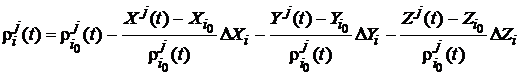 .
.
(111)
Aceasta ecuatie este o functie liniara de necunoscutele ![]() .
.
3.2 Modelul liniar pentru pozitionarea absoluta pe baza
cod-distantelor
Modelul este dat doar in forma sa elementara, influentele ionosferei, troposferei precum si altor surse de erori minore fiind neglijate. Conform ecuatiei (8.5), modelul pentru pozitionarea absoluta pe baza cod-distantelor masurate este
![]() , (112)
, (112)
care poate fi imediat liniarizat substituind (111):
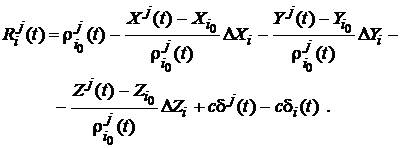 (113)
(113)
Prin separarea in partea dreapta a termenilor necunoscuti, aceasta relatie capata aspectul
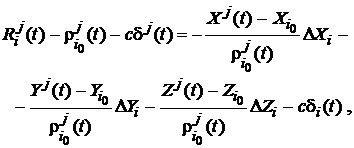 (114)
(114)
eroarea de ceas al satelitului fiind considerata deci
cunoscuta. Acest lucru decurge din faptul ca mesajul de navigatie transmis de
satelit contine coeficientii polinomului de evaluare a acestei erori (vezi
5.1.2). Modelul (114) contine, pentru epoca t,
patru necunoscute : ![]() . Ca urmare, pentru rezolvarea problemei sunt necesari patru
sateliti. Pentru scrierea mai comoda a sistemului de ecuatii efectuam notatiile
. Ca urmare, pentru rezolvarea problemei sunt necesari patru
sateliti. Pentru scrierea mai comoda a sistemului de ecuatii efectuam notatiile
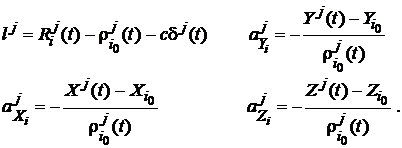 (115)
(115)
Sistemul de ecuatii va fi
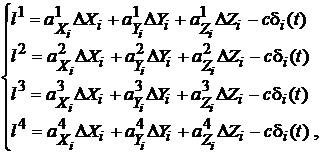 (116)
(116)
indicii superiori fiind utilizati pentru identificarea celor patru sateliti (nu au sensul de exponenti !). Introducand si notatiile
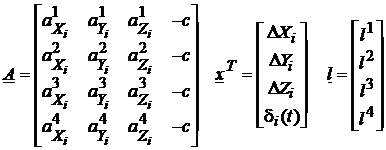 , (117)
, (117)
sistemul de ecuatii in forma matriceala va fi:
![]() . (118)
. (118)
Pentru acest prim exemplu de liniarizare a modelului
observatiilor GPS, vectorul ![]() si matricea
si matricea ![]() , explicitate pentru epoca t sunt:
, explicitate pentru epoca t sunt:
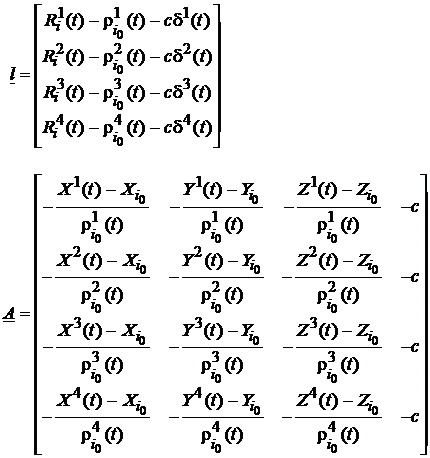 (119)
(119)
Sistemul (118) nu necesita o analiza detaliata. Prin
rezolvarea lui se obtin corectiile coordonatelor punctului ![]() si eroarea de ceas a
receptorului
si eroarea de ceas a
receptorului ![]() , pentru epoca observatiilor t. Coordonatele definitive ale punctului se obtin cu (108).
, pentru epoca observatiilor t. Coordonatele definitive ale punctului se obtin cu (108).
Pozitionarea absoluta pe baza cod-distantelor este aplicabila separat pentru fiecare epoca. Din acest motiv, acest mod de compensare este utilizat in aplicatiile cinematice.
3.3 Modelul liniar pentru pozitionarea absoluta pe baza
masuratorilor de faza
Procedura
este asemanatoare celei prezentata anterior. In ecuatia (8.8), ![]() este liniarizat apoi
termenii cunoscuti sunt trecuti in partea stanga. Se obtine relatia
este liniarizat apoi
termenii cunoscuti sunt trecuti in partea stanga. Se obtine relatia
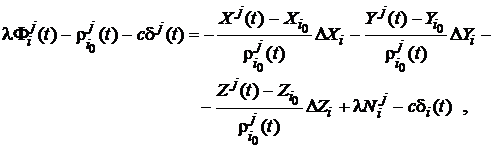 (120)
(120)
in care numarul necunoscutelor este marit de ambiguitati. Considerand inca o data cazul clasic (4 sateliti), componentele sistemului matriceal (118) vor fi:
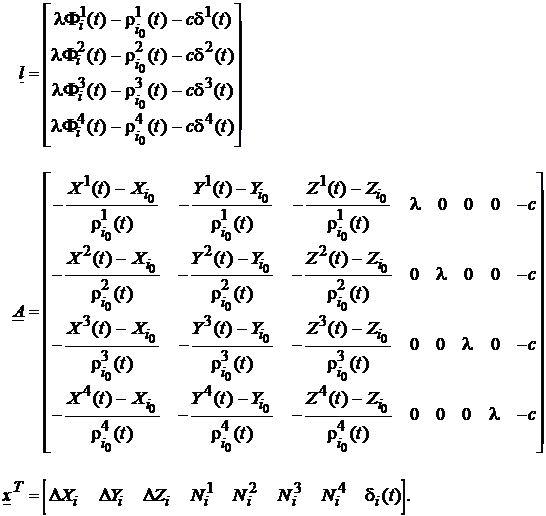
(121)
Evident, aceste patru
ecuatii nu sunt suficiente pentru determinarea celor opt necunoscute. De aici rezulta ca pozitionarea nu se poate face
pe baza observatiilor executate la o singura epoca. Pentru fiecare epoca in
plus, numarul necunoscutelor creste cu una (corectia de ceas al receptorului).
Deci pentru doua epoci avem opt ecuatii cu noua necunoscute (tot
nedeterminare). Pentru trei epoci se scriu 12 ecuatii cu 10 necunoscute,
sistemul fiind deja supradeterminat. Aceste necunoscute sunt: corectiile
coordonatelor punctului notate ![]() , ambiguitatile intregi ale celor patru sateliti notate
, ambiguitatile intregi ale celor patru sateliti notate ![]() si corectiile de ceas
al receptorului aferente celor trei momente de observatii -
si corectiile de ceas
al receptorului aferente celor trei momente de observatii - ![]() ,
, ![]() ,
, ![]() . Introducand notatiile
. Introducand notatiile
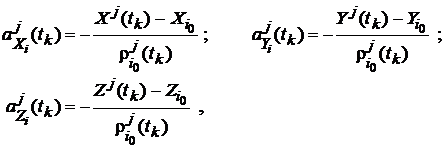 (122)
(122)
elementele sistemului matricial vor avea expresiile:
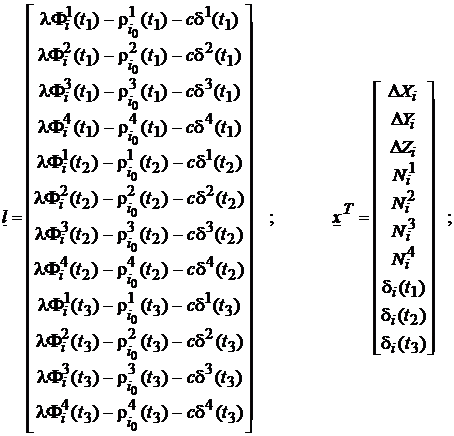
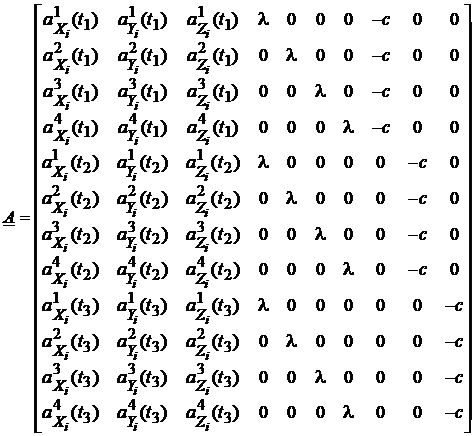 (123)
(123)
Rezolvarea acestui sistem supradeterminat trebuie facuta cu metoda celor mai mici patrate, descrisa la punctul 2.
3.4 Modelul liniar pentru pozitionarea relativa
Pentru pozitionarea relativa trebuie studiat numai cazul masuratorilor de faza. Liniarizarea ecuatiilor de observatii si chiar alcatuirea sistemului de ecuatii raman in principiu aceleasi pentru prelucrari ale fazelor sau ale combinatiilor de faze. In continuare se va prezenta in detaliu numai cazul diferentelor duble. Conform ecuatiei (8.22), modelul diferentelor duble este
![]() , (124)
, (124)
unde termenul ![]() continand pozitiile
este dat de relatia
continand pozitiile
este dat de relatia
![]() , (125)
, (125)
deci contine cele patru masuratori necesare pentru formarea unei diferente duble.
Fiecare din cei patru termeni poate fi liniarizat in conformitate cu (111), conducand in final la:
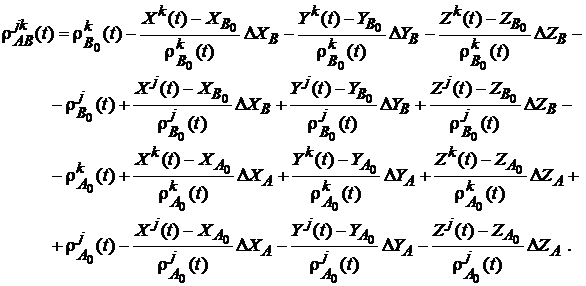
(126)
Pentru a putea da o forma lizibila sistemului de ecuatii
de forma ![]() , introducem notatiile
, introducem notatiile
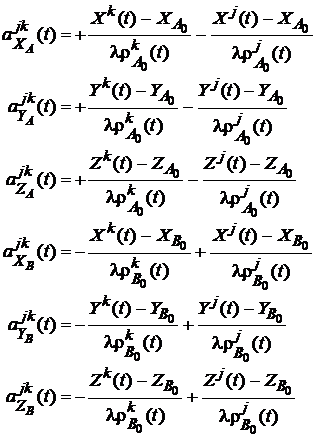 (127)
(127)
precum si, pentru pentru partea stanga,
![]() . (128)
. (128)
Acest termen contine atat masuratorile cat si termenii calculati cu valorile aproximative. Cu notatiile (127) si (128), ecuatia de observatii liniarizata va fi
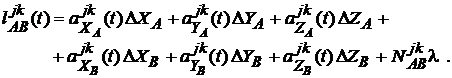 (129)
(129)
Evident, in aceasta ecuatie intervin doua puncte necunoscute (capetele liniei de baza). Pozitionarea relativa a punctului B in raport cu A se face insa considerand punctul A cunoscut, adica
![]() , (130)
, (130)
lucru care conduce la reducerea numarului necunoscutelor cu trei si la mici modificari in expresia termenului din partea stanga:
![]() . (131)
. (131)
Considerand
acum patru sateliti j, k, l,
m si doua epoci ![]() , componentele sistemului matriceal vor fi:
, componentele sistemului matriceal vor fi:
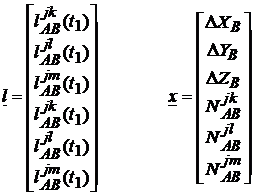
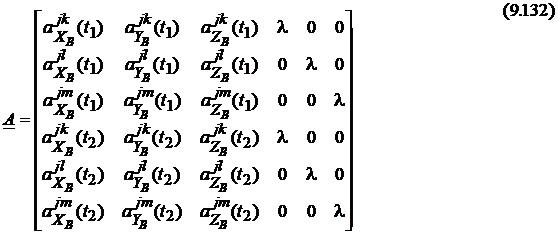
Sistemul este determinat, deci rezolvabil. Este de retinut faptul ca pentru o singura epoca numarul necunoscutelor este mai mare decat cel al ecuatiilor.
4 Compensarea retelelor
4.1 Solutia 'un singur vector'
Compensarea
propriu-zisa consta in gasirea solutiilor sistemului de ecuatii liniare cu
respectarea principiului celor mai mici patrate (![]() ), care impune cunoasterea matricii ponderilor. Deoarece
procesele de compensare sunt bine cunoscute de toti inginerii geodezi, in cele
ce urmeaza vor fi facute doar cateva observatii.
), care impune cunoasterea matricii ponderilor. Deoarece
procesele de compensare sunt bine cunoscute de toti inginerii geodezi, in cele
ce urmeaza vor fi facute doar cateva observatii.
Asa cum a fost aratat la punctul 8.2.2, fazele masurate si diferentele simple sunt necorelate iar diferentele duble si diferentele triple sunt corelate. Implementarea corelatiilor diferentelor duble este destul de simpla; se poate executa si o decorelare a acestora, folosind o ortonormalizare Gram-Schmidt. Pentru diferentele triple, implementarea corelatiilor este ceva mai dificila. Se pune chiar problema daca merita depus efortul de obtinere a corelatiilor diferentelor triple de vreme ce zgomotul acestor diferente nu permite obtinerea unei solutii exacte.
In cazul
observatiilor executate intr-o retea, metoda un singur vector presupune calculul vector cu vector, pentru toate
combinatiile posibile. Daca ![]() este numarul punctelor
stationate, atunci pot fi calculate
este numarul punctelor
stationate, atunci pot fi calculate ![]() linii de baza. Dintre
acestea numai
linii de baza. Dintre
acestea numai ![]() sunt teoretic
independente. Liniile redundante pot fi folosite pentru cercetarea inchiderilor
pe contururi poligonale (deci depistarea liniilor gresite) sau pentru o
compensare aditionala a vectorilor bazelor.
sunt teoretic
independente. Liniile redundante pot fi folosite pentru cercetarea inchiderilor
pe contururi poligonale (deci depistarea liniilor gresite) sau pentru o
compensare aditionala a vectorilor bazelor.
Exista
si alte moduri de abordare. De exemplu, calculele pot fi restrictionate la ![]() vectori, atent
selectionati. O alta metoda ia in considerare existenta a mai multe sesiuni de
observatii. Pentru fiecare sesiune sunt calculate toate liniile de baza
posibile, apoi vectorii rezultati din toate sesiunile sunt supusi unei
compensari in bloc.
vectori, atent
selectionati. O alta metoda ia in considerare existenta a mai multe sesiuni de
observatii. Pentru fiecare sesiune sunt calculate toate liniile de baza
posibile, apoi vectorii rezultati din toate sesiunile sunt supusi unei
compensari in bloc.
Dezavantajul principal al metodei un singur vector consta in faptul ca, din punct de vedere teoretic, solutia nu este corecta deoarece intre liniile de baza masurate simultan (intr-o sesiune) exista corelatii; aceste corelatii sunt ignorate la rezolvarea vector cu vector. Intercorelatiile intre liniile de baza vor fi tratate la punctul urmator.
4.2 Solutia 'multipunct'
Spre deosebire de cazul precedent, aici toate ponctele retelei sunt analizate simultan. Diferenta fundamentala consta in aceea ca aici sunt luate in considerare corelatiile intre liniile de baza.
Principalele corelatii au fost prezentate la punctul 8.2.2. Aceleasi aspecte teoretice pot fi extinse pentru cazul unei retele. In continuare vor fi prezentate niste exemple simple, pentru a se evita aparitia unor formule stufoase.
Exemplu de retea prelucrata cu diferente simple. Presupunem trei puncte de statie A, B, C din care a fost observat un singur satelit j, la o singura epoca t. Pot fi definite doua linii de baza independente. Luand A ca statie de referinta, pentru cele doua linii de baza A-B si A-C, satelitul j si epoca t pot fi formate doua diferente simple:
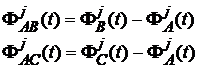 (133)
(133)
Introducand notatiile
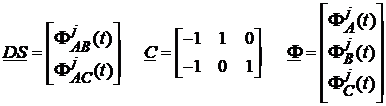 , (134)
, (134)
sistemul (33) poate fi scris matriceal ca ![]() . Pentru aflarea corelatiilor, aplicand legea de propagare a
covariantei
. Pentru aflarea corelatiilor, aplicand legea de propagare a
covariantei ![]() obtinem
obtinem
![]() , (135)
, (135)
deoarece conform relatiei (8.32), ![]() . Daca in (135) inlocuim matricea
. Daca in (135) inlocuim matricea ![]() cu expresia sa data de
(134) si efectuam inmultirea cu transpusa ei, rezulta
cu expresia sa data de
(134) si efectuam inmultirea cu transpusa ei, rezulta
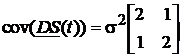 . (136)
. (136)
Acest rezultat arata ca cele doua diferente simple sunt corelate, lucru asteptat deoarece la formarea lor a contribuit un punct comun. Trebuie reamintit faptul ca la calculul unui singur vector, asa cum s-a aratat la punctul 8.2.2, diferentele simple nu sunt corelate.
Exemplu de retea prelucrata cu diferente triple. Deoarece diferentele simpe sunt corelate pentru un singur vector de baza, este de asteptat sa apara corelatii si in retea. Presupunem din nou trei puncte de statie A, B, C. Daca A este statie de referinta, bazele vor fi A-B si A-C. La o singura epoca t au fost observati patru sateliti j, k, l, m, j fiind considerat satelit de referinta.
Pentru ![]() puncte si
puncte si ![]() sateliti pot fi
formate
sateliti pot fi
formate ![]() diferente duble
independente. In exemplul considerat,
diferente duble
independente. In exemplul considerat, ![]() si
si ![]() , deci pot fi formate sase diferente duble. Conform ecuatiei
(8.25), acestea sunt:
, deci pot fi formate sase diferente duble. Conform ecuatiei
(8.25), acestea sunt:
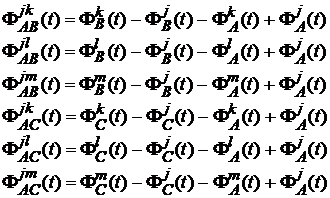 (137)
(137)
Pentru o exprimare matriceala a sistemului, mai comoda, introducem notatiile:
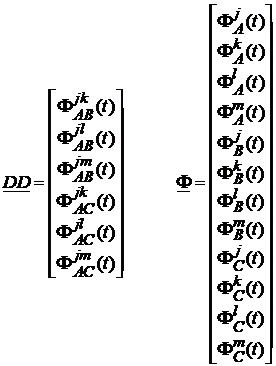
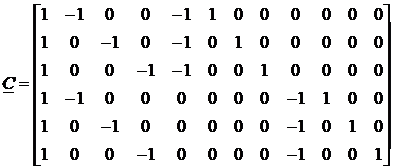 (138)
(138)
Sistemul poate fi scris:
![]() . (139)
. (139)
Matricea de covarianta este data de relatia
![]() (140)
(140)
care, avand in vedere ca fazele nu sunt corelate, se reduce la
![]() . (141)
. (141)
Produsul ![]() explicitat este o
matrice plina,
explicitat este o
matrice plina,
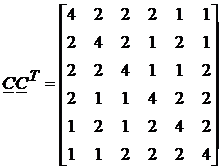 , (142)
, (142)
prin a carei inversare se obtine matricea ponderilor:
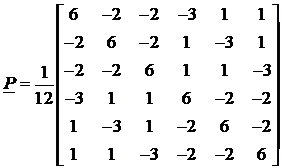 (143)
(143)
S-au efectuat diverse experimente pentru stabilirea importantei luarii in consideratie a corelatiilor. Pentru retele mici si cu laturi scurte (pana la 10 km), neglijarea corelatiilor conduce la erori de ordinul milimetrilor.
4.3 Comparatie intre metoda 'un singur vector de baza
si solutia 'multipunct'
Alegerea uneia sau alteia dintre metodele de prelucrare ar putea fi influentata de diverse consideratii, cateva dintre acestea fiind:
Metoda 'un singur vector de baza' nu permite modelarea optima a corelatiilor, deoarece intercorelatiile intre vectorii de baza sunt neglijate.
Programarea pe calculator este mult mai comoda la metoda 'un singur vector de baza'.
Timpul de calcul nu constituie o problema deosebita, programele performante rulate pe calculatoare puternice permitand obtinerea unei baze in cateva minute.
Alunecarile de cicli sunt mai usor de detectat si de corectat in modul 'multipunct'.
Identificarea vectorilor mai slab determinati este foarte comoda pentru 'un singur vector de baza', existand implicit si posibilitatea eliminarii lor.
Implementarea completa a corelatiilor la solutia 'multipunct' functioneaza numai in retelele in care observatiile executate in toate punctele se incadreaza aproximativ in acelasi sablon. Daca exista un numar apreciabil de abateri, este preferabil sa se calculeze corelatiile pe baza schitei retelei.
Chiar si in cazul abordarii 'multipunct', este discutabila modelarea corecta a tuturor corelatiilor (de exemplu in cazul efectuarii, in aceeasi retea, a unor masuratori pe frecventa duala -care elimina refractia ionosferica- si a unora numai pe L1).
5 Pierderea preciziei
Pozitia reciproca a satelitilor vizibili constituie un factor cu consecinte importante asupra calitatii rezultatelor, in special pentru pozitionarea absoluta si pentru determinarile cinematice. Pozitia reciproca se schimba permanent, datorita miscarii satelitilor pe orbitele lor. Pentru evaluarea influentei dispunerii geometrice a satelitilor se utilizeaza factorul DOP (Dilution of Precision), a carui definire va fi explicata in continuare.
Pentru
inceput consideram ca sunt observati patru sateliti. In cazul pozitionarii
absolute pe baza pseudodistantelor, ecuatiile de observatii liniarizate sunt
date de (118) iar cele patru necunoscute se obtin cu relatia inversa ![]() . Aspectul matricii
. Aspectul matricii ![]() este dat de (119),
este dat de (119),
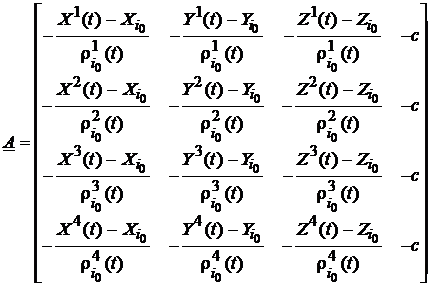 , (144)
, (144)
in care primele trei elemente din fiecare linie definesc
vectorii unitari ![]() , j=1,2,3,4
orientati din cei patru sateliti spre punctul de statie. Rezolvarea nu este
posibila daca matricea
, j=1,2,3,4
orientati din cei patru sateliti spre punctul de statie. Rezolvarea nu este
posibila daca matricea ![]() este singulara, altfel
spus daca determinantul este nul. Determinantul este proportional cu produsul
scalar triplu
este singulara, altfel
spus daca determinantul este nul. Determinantul este proportional cu produsul
scalar triplu
![]() ,
,
care din punct de vedere geometric exprima volumul
corpului format de intersectia vectorilor statie-sateliti cu sfera de raza
unitara avand centrul in punctul de statie. Cu cat acest volum este mai mare,
cu atat dispunerea satelitilor este mai buna. O buna conformatie geometrica
trebuie sa conduca la pierderi mici de precizie, deci valoarea DOP este
proportionala cu invesa volumului corpului. Configuratia critica apare atunci
cand corpul degenereaza intr-un plan. Acest lucru se intampla cand vectorii ![]() formeaza un con cu
varful in punctul de statie.
formeaza un con cu
varful in punctul de statie.
In cazul
general, valoarea DOP poate fi calculata prin inversarea matricii ecuatiilor
normale. Matricea cofactorilor ![]() rezulta din
rezulta din
![]() . (145)
. (145)
In acest caz, matricea ponderilor poate fi luata ca
matricea unitate. Matricea cofactorilor ![]() este de dimensiuni
este de dimensiuni ![]() , componentele sale caracterizand pozitia statiei (X,Y,Z) si ceasul receptorului. Notand
elementele matricei cofactorilor cu
, componentele sale caracterizand pozitia statiei (X,Y,Z) si ceasul receptorului. Notand
elementele matricei cofactorilor cu
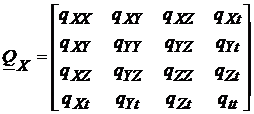 , (146)
, (146)
elementele diagonalei principale servesc la definirea urmatoarelor marimi DOP:
![]() pierderea
geometrica a preciziei;
pierderea
geometrica a preciziei;
![]() pierderea preciziei pozitiei;
pierderea preciziei pozitiei;
![]() pierderea preciziei temporale.
pierderea preciziei temporale.
(147)
Trebuie retinut ca explicatiile date mai sus asupra DOP (folosind corpul geometric) se refera la GDOP.
In (147),
valorile DOP sunt exprimate in sistemul ecuatorial ECEF. Daca se doreste
exprimarea intr-un sistem topocentric cu axele dirijate spre nord, est si
zenit, atunci atunci matricea globala ![]() trebuie transformata
intr-o matrice locala a cofactorilor
trebuie transformata
intr-o matrice locala a cofactorilor ![]() , folosind legea de propagare a covariantei. Notand cu
, folosind legea de propagare a covariantei. Notand cu ![]() acea parte a matricii
cofactorilor care contine componentele geometrice (deci renuntand la elementele
ce contin timpul), transformarea va fi data de relatia
acea parte a matricii
cofactorilor care contine componentele geometrice (deci renuntand la elementele
ce contin timpul), transformarea va fi data de relatia
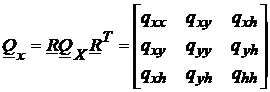 , (148)
, (148)
in care matricea de rotatie ![]() contine axele
sistemului local de coordonate, date de (10.51).
contine axele
sistemului local de coordonate, date de (10.51).
Pentru un PDOP local pot fi definite doua marimi DOP aditionale care caracterizeaza pierderile in precizia planimetrica respectiv altimetrica:
![]() pierderea
preciziei potitionarii orizontale
pierderea
preciziei potitionarii orizontale
![]() pierderea preciziei potitionarii
verticale.
pierderea preciziei potitionarii
verticale.
Pana in prezent a fost analizat numai cazul masuratorilor efectuate la o singura epoca. In etapa de planificare a efectuarii masuratorilor este important sa se cunoasca valorile DOP pentru intreaga durata a fiecarei sesiuni de observatii. Pentru acest lucru se intocmeste un grafic, pe baza valorilor DOP calculate pentru diverse epoci distantate la un interval convenabil ales. Un exemplu este dat in figura 5, unde sunt reprezentate valorile PDOP pentru o zi intreaga de observatii, calculele fiind facute cu un interval intre epoci de 15 minute. Pentru efectuarea calculelor nu se folosesc date de masurare ci elementele orbitale aproximative continute in fisierul cu date de almanah (almanac data), transmise prin mesajul de navigatie. Valorile DOP sunt folosite nu numai pentru pozitionarea absoluta ci si pentru determinarile relative, in acest caz ele fiind considerate ca valori DOP relative.
Pe langa importanta deosebita avuta in planificarea executarii masuratorilor, valorile DOP sunt foarte utile in interpretarea datelor la prelucrarea vectorilor de baza. De exemplu, datele cu un DOP slab pot fi eliminate de la inceput, pentru a nu influenta precizia rezultatelor finale.
Dupa
efectuarea prelucrarilor, se pot interpreta rezultatele pe baza legaturii care
exista intre DOP si acuratetea pozitionarii. Daca abaterea standard a
masuratorilor este ![]() atunci precizia pozitionarii este data de
produsul dintre
atunci precizia pozitionarii este data de
produsul dintre ![]() si valoarea DOP:
si valoarea DOP:
![]() . (150)
. (150)
Aplicand aceasta formula pentru valorile DOP definite anterior obtinem:
GDOP![]() precizia
geometrica in pozitie si timp;
precizia
geometrica in pozitie si timp;
GDOP![]() precizia
pozitionarii;
precizia
pozitionarii;
GDOP![]() precizia
timpului;
precizia
timpului;
GDOP![]() precizia
pozitionarii planimetrice;
precizia
pozitionarii planimetrice;
GDOP![]() precizia
pozitionarii altimetrice.
precizia
pozitionarii altimetrice.
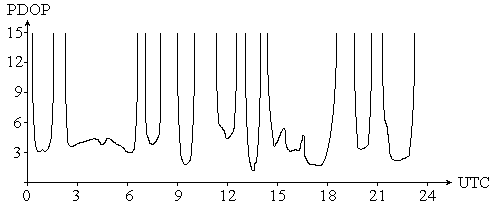
Figura 5. Reprezentarea grafica a PDOP
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||
|
||||||||||
Referate pe aceeasi tema
| ||||||||||
|
| ||||||||||
|
||||||||||
|
|
||||||||||








