
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Matlab
|
|
Qdidactic » stiinta & tehnica » informatica » matlab Reprezentarea polinoamelor. Interpolarea |
Reprezentarea polinoamelor. Interpolarea
Reprezentarea polinoamelor. Interpolarea
Polinoame
MATLAB-ul furnizeaza functii pentru operatii polinomiale standard cum ar fi calculul radacinilor, evaluarea polinoamelor, derivarea etc. O parte din aceste operatii precum si modul de reprezentare a polinoamelor ca vectori au fost descrise in capitolul de Fundamente de programare.
Functiile polinomiale se afla in directorul polyfun:
|
Functie |
Descriere |
|
|
Multiplica polinoamele. |
|
|
Imparte polinoamele. |
|
|
Returneaza coeficientii daca se dau radacinile; Polinomul caracteristic. |
|
|
Calcul derivatei unui polinom. |
|
|
Gasirea coeficientilor unui polinom din aproximarea unui set de date. |
|
|
Evaluarea unui polinom. |
|
|
Evaluarea unui polinom cu argument matriceal. |
|
|
Descompunere in fractii simple. |
|
|
Gasirea radacinilor unui polinom. |
q Dupa cum s-a precizat deja, MATLAB-ul reprezinta polinoamele ca vectori linie care contin coeficientii polinoamelor in ordinea descrescatoare a puterilor.
q Functiile uzuale care opereaza cu polinoame au fost prezentate (de exemplu roots). In continuare sunt parcurse alte cateva exemple utile. v Functia
poly returneaza
coeficientii unui polinom daca dispunem de radacinile
acestuia (este o functie inversa fata de roots):
» p=[1 -1 2 4 1];
» r=roots(p)
r =
1.0529 + 1.7248i
1.0529 - 1.7248i
-0.7995
-0.3063
» coef=poly(r)
coef =
1.0000 -1.0000 2.0000 4.0000 1.0000
O
alta utilizare a functiei poly este
aceea de calculare a coeficientilor polinomului caracteristic al unei
matrice:
A =
-1 -3 1
2 -2 -1
0 1 -3
» poly(A)
ans =
1 6 18 23
Radacinile acestui polinom sunt chiar valorile
proprii ale matricii A
|
v
Functia
polyval evalueaza un polinom pentru
o valoare specificata a argumentului.
Functia polyvalm permite evaluarea unui polinom in sens matriceal. In acest caz polinomul p din exemplul anterior: p(x) = x4 – x3 + 2x2 + 4x + 1 devine p(X) = X4 – X3 + 2X2 + 4X + I, unde X este o matrice patratica si I matricea unitate.
Exemplu:
» C=polyvalm(p,A)C =
-75 -61 81
58 -130 75
52 -23 49
v
Functiile
conv si deconv implementeaza
operatiile de inmultire si impartire a polinoamelor.
Exemple:
Fie a(x) = x2 + 2x +3 si b(x) = 4x2 + 5x + 6.
» a = [1 2 3]; b = [4 5 6];
» c = conv(a,b)
c =
4 13 28 27 18
» [q,r] = deconv(c,a)
q =
4 5 6
r =
0 0 0 0 0
v Functia polyder permite
calculul derivatei unui polinom.
Exemplu:
» p=[1 -1 2 4 1];
» pderivat=polyder(p)
pderivat =
4 -3 4 4
v Functia polyfit
gaseste coeficientii unui polinom (o curba) care
aproximeaza un set de date in sensul algoritmului celor mai mici
patrate:
p = polyfit(x,y,n)
x si y sunt vectorii care contin
setul de date iar n este ordinul polinomului ai
carui coeficienti vor fi furnizati la apelarea functiei.
Exemplu:
» x = [1 2 3 4 5]; y = [5.5 43.1 128 290.7 498.4];
» p = polyfit(x,y,3)
p =
-0.1917 31.5821 -60.3262 35.3400
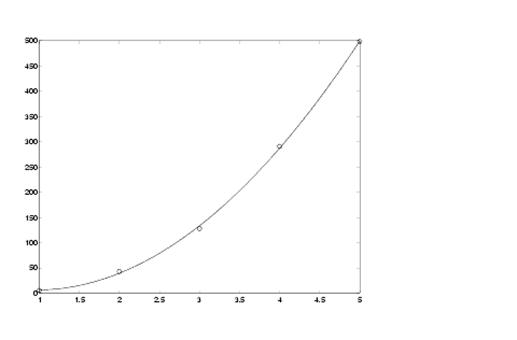
Pentru plotarea rezultatului se utilizeaza mai intai
functia polyval pentru o trasare cat mai
exacta a graficului polinomului si apoi se ploteaza estimarea
versus datele reale pentru comparatii.
» x2 = 1:.1:5;
» y2 = polyval(p,x2);
» plot(x,y,'o',x2,y2)
v Functia residue se
utilizeaza pentru descompunerea in fractii simple.
Se aplica in cazul raportului a doua polinoame b si a
![]()
unde r este un vector coloana, p tot un vector coloana care contine polii iar k un vector linie cu termenii directi.
Exemplu:
![]()
» b = [-4 8];
» a = [1 6 8];
» [r,p,k] = residue(b,a)
r =
-12
8
p =
-4
-2
k =
[]
Daca
se folosesc trei argumente de intrare (r p, si k),
functia residue
asigura conversia inapoi in forma polinomiala:
» [b2,a2] = residue(r,p,k)
b2 =
-4 8
a2 =
1 6 8
Interpolarea
Interpolarea este un proces de estimare a valorilor dintre date (puncte) cunoscute. Aplicatiile interpolarii sunt numeroase in domenii cum ar fi procesarea numerica a semnalelor si imaginilor.
MATLAB-ul dispune de mai multe tehnici de interpolare, alegerea unei metode sau alteia facandu-se in functie de acuratetea necesara, de viteza de executie si de gradul de utilizare a memoriei.
Functiile
de interpolare se afla in directorul polyfun
|
Functie |
Descriere |
|
|
Interpolare pe suprafete. |
|
|
Interpolare monodimensionala. |
|
|
Interpolare bi-dimensionala. |
|
|
Interpolare tri-dimensionala. |
|
|
Interpolare mono utilizand metoda FFT. |
|
|
Interpolare spline (cubica). |
Compararea unor metode de interpolare bi-dimensionala
In continuare este preluat si prezentat (informativ) un exemplu de folosire a unor metode de interpolare bi-dimensionala pentru o matrice de date 7 x 7.
- Generarea functiei peaks (cu rezolutie mica):
z = peaks(x,y);
surf(x,y,z)
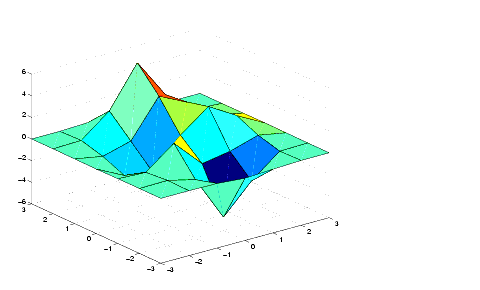
- Generarea unei suprafete mesh fine pentru interpolare:
- Interpolarea cu metoda celei mai apropiate vecinatati:
- Interpolarea cu metoda biliniara:
- Interpolarea cu metoda bicubica:
- Compararea graficelor corespunzatoare diferitelor metode de interpolare:
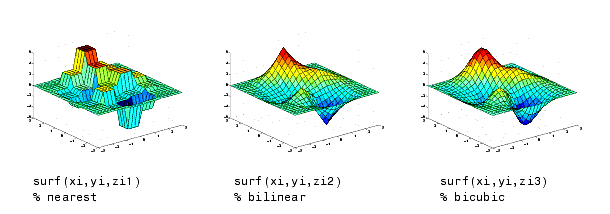
Compararea
contururilor suprafetelor in cazul diferitelor metode de interpolare:
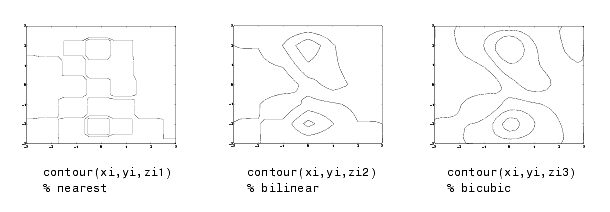
Se observa ca metoda bicubica produce cele mai netede contururi. O metoda cum ar fi cea a celor mai apropiate vecinatati este preferata insa in anumite aplicatii, cum ar fi cele medicale unde nu trebuie generate date noi.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Lucrari pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








