| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica DC Motor - DC Machine - speed control of shunt dc motors |
DC Motor - DC Machine - speed control of shunt dc motors
DC MOTORS
Summary:
The Equivalent Circuit of a DC Motor
The Magnetization Curve of a DC Machine
Separately Excited and
The Terminal Characteristics of a Shunt DC Motor
Nonlinear Analysis of a Shunt DC Motor
Speed Control of
The Effect of an Open Field Circuit
The Permanent-Magnet DC Motor
The Series DC Motor
Induced Torque in a Series DC Motor
The Terminal Characteristic of a Series DC Motor
Speed Control of Series DC Motors.
The Compounded DC Motor
The Torque-Speed Characteristic of a Cumulatively Compounded DC Motor
The Torque-Speed Characteristic of a Differentially Compounded DC Motor
The Nonlinear analysis of Compounded DC Motors
Speed Control in the Cumulatively Compounded DC Motor
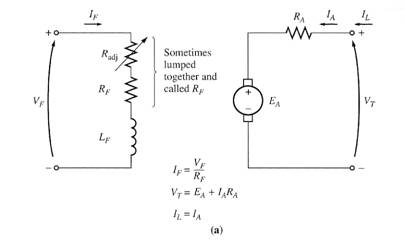
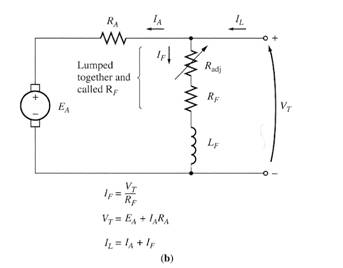
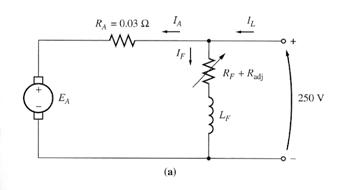
The Equivalent Circuit of a DC Motor
(a) The equivalent circuit (b) A simplified equivalent circuit
eliminating the brush voltage drop and combining Radj with the
field resistance.
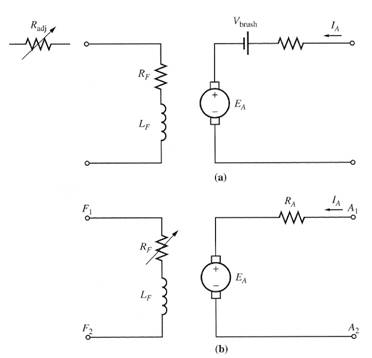
In this figure, the armature circuit is represented by an ideal voltage source EA and a resistor RA. This representation is really the Thevenin equivalent of the entire rotor structure, including rotor coils, interpoles and compensating windings, if present.
The brush voltage drop is represented by a small battery Vbrush opposing the direction of current flow in the machine.
The field coils, which produce the magnetic flux in the motor are represented by inductor LF and resistor RF. The separate resistor Radj represents an external variable resistor used to control the amount of current in the field circuit.
Some of the few variations and simplifications:
i- The brush drop voltage is often only a very tiny fraction of the generated voltage in the machine. Thus, in cases where it is not too critical, the brush drop voltage may be left out or included in the RA.
ii- The internal resistance of the field coils is sometimes lumped together with the variable resistor and the total is called RF.
iii- Some generators have more than one field coil, all of which appear on the equivalent circuit.
The internal generated voltage is given by:
EA = K
and the torque induced is
t
The Magnetization Curve of a DC Machine
EA is directly proportional to flux and the speed of rotation of the machine. How is the EA related to the field current in the machine?
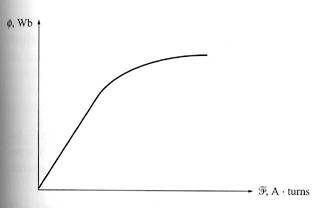
The field current in a dc machine produces a field mmf given by F=NFIF. This mmf produces a flux in the machine in accordance with its magnetization curve, shown below:
The
magnetization curve of a ferromagnetic material
Since the field current is directly proportional to the mmf and since EA is directly proportional to flux, it is customary to present the magnetization curve as a plot of EA vs field current for a given speed
The
magnetization curve of a dc machine expressed as a plot of EA versus
IF for a fixed speed wo.
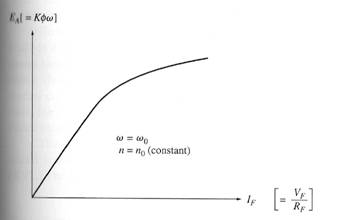
NOTE: Most machines are designed to operate near the saturation point on the magnetization curve. This implies that a fairly large increase in field current is often necessary to get a small increase in EA when operation is near full load.
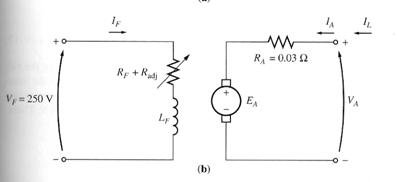
Separately Excited and
The equivalent
circuit of a separately excited dc motor The equivalent
circuit of a shunt dc motor
A separately excited dc motor is a motor whose field circuit is supplied from a separate constant-voltage power supply, while a shunt dc motor is a motor whose field circuit gets its power directly across the armature terminals of the motor.
When the supply voltage to a motor is assumed constant, there is no practical difference in behaviour between these two machines. Unless otherwise specified, whenever the behaviour of a shunt motor is described, the separately excited motor is included too.
The KVL equation for the armature circuit is:
VT = EA + IARA
The Terminal Characteristics of a Shunt DC Motor
A terminal characteristic of a machine is a plot of the machine's output quantities versus each other. For a motor, the output quantities are shaft torque and speed, so the terminal characteristic of a motor is a plot of its output torque versus speed.
How does a shunt dc motor respond to a load?
Suppose that the load on the shaft of a shunt motor is
increased. Then the load torque tload will
exceed the induced torque t
The output characteristic of a shunt dc motor can be derived from the induced voltage and torque equations of the motor plus the KVL.
KVL VT = EA + IARA
The induced voltage EA = Kso
VT = K + IARA
Since t
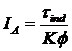
Combining the VT and IA equations:
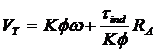
|
Finally, solving for the motor's speed:
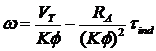
 This
equation is just a straight line with a negative slope. The resulting torque-speed characteristic of
a shunt dc motor is shown here:
This
equation is just a straight line with a negative slope. The resulting torque-speed characteristic of
a shunt dc motor is shown here:
Torque-speed
characteristic of a shunt or separately excited dc motor with compensating
windings to eliminate armature reaction
It is important to realize that, in order for the speed of the motor to vary linearly with torque, the other terms in this expression must be constant as the load changes. The terminal voltage supplied by the dc power source is assumed to be constant - if it is not constant, then the voltage variations will affect the shape of the torque-speed curve.
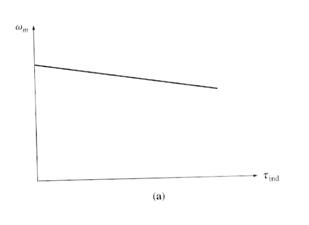
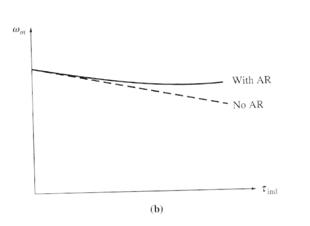 Another
effect internal to the motor that can also affect the shape of the torque-speed
curve is armature reaction. If a motor
has armature reaction, then as its load increases, the flux-weakening effects
reduce its flux. From the motor speed
equation above, the effect of reduction in flux is to increase the motor's
speed at any given load over the speed it would run at without armature
reaction. The torque-speed
characteristic of a shunt motor with armature reaction is shown below:
Another
effect internal to the motor that can also affect the shape of the torque-speed
curve is armature reaction. If a motor
has armature reaction, then as its load increases, the flux-weakening effects
reduce its flux. From the motor speed
equation above, the effect of reduction in flux is to increase the motor's
speed at any given load over the speed it would run at without armature
reaction. The torque-speed
characteristic of a shunt motor with armature reaction is shown below:
Torque-speed
characteristic of the motor with armature reaction present.
If a motor has compensating windings, there will be no flux weakening problems and the flux in the motor will be constant.
If a shunt dc motor has compensating windings so that flux is constant regardless of load, and the motor's speed and armature current are known at any one value of load, then it is possible to calculate its speed at any other value of load, as long as the armature current at that load is known or can be determined.
Example 9.1
A 50HP, 250V, 1200 r/min DC shunt motor with compensating windings has an armature resistance (including the brushes, compensating windings, and interpoles) of 0.06 W Its field circuit has a total resistance Radj + RF of 50 W, which produces a no-load speed of 1200r/min. There are 1200 turns per pole on the shunt field winding (Figure below)
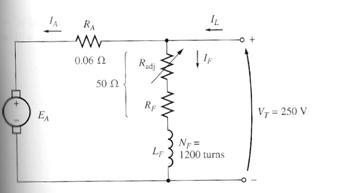
(a) Find the speed of this motor when its input current is 100A.
(b) Find the speed of this motor when its input current is 200A.
(c) Find the speed of this motor when its input current is 300A.
Nonlinear Analysis of a Shunt DC Motor
The flux and hence the internal generated voltage EA of a dc machine is a non linear function of its magnetomotive force. Therefore, anything that changes the mmf in a machine will have a non linear effect on the EA of the machine. Since the change in EA cannot be calculated analytically, the magnetization curve of the machine must be used. Two principal contributors to the mmf in the machine are its field current and its armature reaction, if present.
Since the magnetization curve is a plot of EA vs IF for a given speed o , the effect of changing a machine's field current can be determined directly from its magnetization curve.
If a machine has armature reaction, its flux will be reduced with each increase in load. The total mmf in a shunt dc motor is the field circuit mmf less the mmf due to armature reaction (AR):
Fnet = NFIF - FAR
Since the magnetization curves are expressed as plots of EA vs field current, it is customary to define an equivalent field current that would produce the same output voltage as the combination of all the mmf in the machine. The resulting voltage EA can then be determined by locating that equivalent field current on the magnetization curve. The equivalent field current:
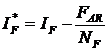
One other effect must be considered when non linear analysis is used to determine EA of a dc motor. The magnetization curves for a machine are drawn for a particular speed, usually the rated speed of the machine. How can the effects of a given field current be determined if the motor is turning at other than rated speed?
The equation for the induced voltage in a dc machine when speed is expressed as rev/min: EA = K'n
For a given effective field current, the flux in the machine is fixed, so the EA is related to speed by:
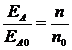
where EA0 and n0 represent the reference values of voltages and speed respectively. If the reference conditions are known from the magnetization curve and the actual EA is known, then it is possible to determine the actual speed n.
Example 9.2
A 50HP, 250V, 1200r/min DC shunt motor without compensating windings has an armature resistance (including the brushes and interpoles) of 0.06 W. Its field circuit has a total resistance Radj + RF of 50 W, which produces a no-load speed of 1200r/min. There are 1200 turns per pole on the shunt field winding, and the armature reaction produces a demagnetising magnetomotive force of 840 A turns at a load current of 200A. The magnetization curve of this machine is shown below:
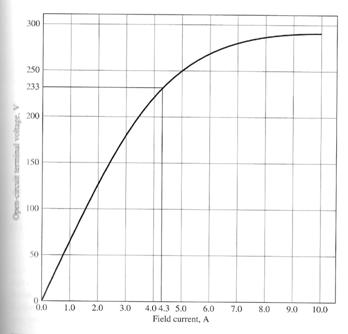
(a) Find the speed of this motor when its input current is 200A.
(b) This motor is essentially identical to the one in Example 9.1 except for the absence of compensating windings. How does its speed compare to that of the previous motor at a load current of 200A?
Speed Control of
Two common methods (as already been seen in Chapter 1 simple linear machine):
i- Adjusting the field resistance RF (and thus the field flux)
ii- Adjusting the terminal voltage applied to the armature.
Less common method:
iii- Inserting a resistor in series with the armature circuit.
Changing the Field Resistance
If the field resistance increases, then the field current decreases (IF↓ = VT/RF↑), and as the field current decreases, the flux decreases as well. A decrease in flux causes an instantaneous decrease in the internal generated voltage EA↓ (=K↓), which causes a large increase in the machine's armature current since,
![]()
The induced torque in a motor is given by t
Look at this example:

Figure above shows a shunt dc motor with an internal resistance of 0.25Ω. It is currently operating with a terminal voltage of 250V and an internal generated voltage of 245V. Therefore, the armature current flow is IA = (250V-245V)/0.25Ω= 20A.
What happens in this motor if there is a 1% decrease in flux? If the flux decrease by 1%, then EA must decrease by 1% too, because EA = K Therefore, EA will drop to:
EA2 = 0.99 EA1 = 0.99 (245) = 242.55V
The armature current must then rise to
IA = (250-242.55)/0.25 = 29.8 A
Thus, a 1% decrease in flux produced a 49% increase in armature current.
So, to get back to the original discussion, the increase in
current predominates over the decrease in flux. so, t
However, as the motor speeds up, EA rises, causing IA
to fall. Thus, induced torque t
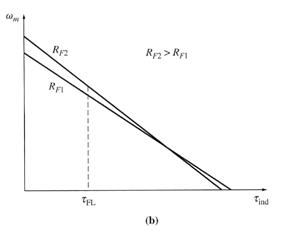
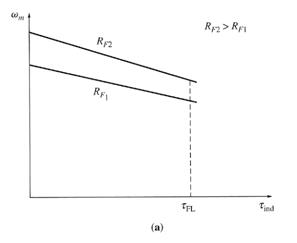
The effect of
field resistance RF speed control on a shunt motor's
torque-speed characteristics. (a) over the motor's normal operating range (b) over the entire range from no load to
stall conditions
WARNING:
The effect of increasing the RF is shown in figure (b) above. Notice that as the flux in the machine decreases, the no-load speed of the motor increases, while the slope of the torque-speed curve becomes steeper.
This figure shows the terminal characteristic of the motor over the full range from no-load to stall conditions. It is apparent that at very slow speeds an increase in field resistance will actually decrease the speed of the motor. This effect occurs because, at very low speeds, the increase in armature current caused by the decrease in EA is no longer large enough to compensate for the decrease in flux in the induced torque equation. With the flux decrease actually larger than the armature current increase, the induced torque decreases, and the motor slows down.
Some small dc motors used for control purposes actually operates at speeds close to stall conditions. For these motors, an increase in RF might have no effect, or it might even decrease the speed of the motor. Since the results are not predictable, field resistance speed control should not be used in these types of dc motors. Instead, the armature voltage method should be employed.
Changing the Armature Voltage
This method involves changing the voltage applied to the armature of the motor without changing the voltage applied to the field.
If the voltage VA is increased, then the IA
must rise [ IA = (VA ↑ -EA)/RA]. As IA increases, the induced
torque t
But, as the speed increases, the EA (=K↑)
increases, causing the armature current to decrease. This decrease in IA decreases the
induced torque, causing t
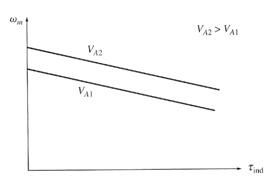
The effect of
armature voltage speed control
Inserting a Resistor in Series with the Armature Circuit
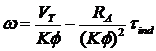 If a
resistor is inserted in series with the armature circuit, the effect is to
drastically increase the slope of the motor's torque-speed characteristic,
making it operate more slowly if loaded. This fact can be seen from the speed equation:
If a
resistor is inserted in series with the armature circuit, the effect is to
drastically increase the slope of the motor's torque-speed characteristic,
making it operate more slowly if loaded. This fact can be seen from the speed equation:
The insertion of a resistor is a very wasteful method of speed control, since the losses in the inserted resistor are very large. For this reason, it is rarely used.
Field Resistance Control
The lower the field current in a shunt (or separately excited) dc motor, the faster it turns: and the higher the field current, the slower it turns. Since an increase in field current causes decrease in speed, there is always a minimum achievable speed by field circuit control. This minimum speed occurs when the motor's field circuit has the maximum permissible current flowing through it.
If a motor is operating at its rated terminal voltage, power and field current, then it will be running at rated speed, also known as base speed. Field resistance control can control the speed of the motor for speeds above base speed but not for speeds below base speed. To achieve a speed slower than base speed by field circuit control would require excessive field current, possibly burning up the field windings.
Armature Voltage Control
The lower the armature voltage on a separately excited dc motor, the slower it turns, and the higher the armature voltage, the faster it turns. Since an increase in armature voltage causes an increase in speed, there is always a maximum achievable speed by armature voltage control. This maximum speed occurs when the motor's armature voltage reaches its maximum permissible level.
If a motor is operating at its rated terminal voltage, power and field current, then it will be running at rated speed, also known as base speed. Armature voltage control can control the speed of the motor for speeds below base speed but not for speeds above base speed. To achieve a speed faster than base speed by armature voltage control would require excessive armature voltage, possibly damaging the armature circuit.
These two techniques of speed control are obviously complementary. Armature voltage control works well for speeds below base speed, and field resistance control works well for speeds above base speed.
There is a significant difference in the torque and power limits on the machine under these two types of speed control. The limiting factor in either case is the heating of the armature conductors, which places an upper limit on the magnitude of the armature current IA.
For armature voltage control, the flux in the motor is constant, so the maximum torque in the motor is tmax =Kmax
This maximum torque is constant regardless of the speed of the rotation of the motor. Since the power out of the motor is given by P=t, the maximum power is Pmax = tmaxThus, the max power out is directly proportional to its operating speed under armature voltage control.
On the other hand, when field resistance control is used, the flux does change. In this form of control, a speed increase is caused by a decrease in the machine's flux. In order for the armature current limit is not exceeded, the induced torque limit must decrease as the speed of the motor increases. Since the power out of the motor is given by P=tand the torque limit decreases as the speed of the motor increases, the max power out of a dc motor under field current control is constant, while the maximum torque varies as the reciprocal of the motor's speed.
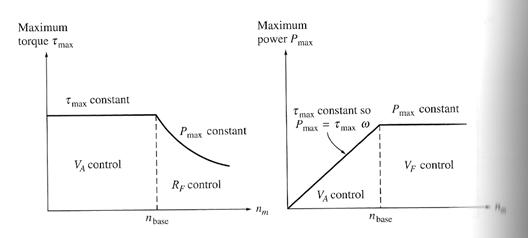
Power and torque limits as a function of speed for a shunt motor under armature voltage and field resistance control
 Example
9.3
Example
9.3
Figure above shows a 100hp, 250 V, 1200 r/min shunt dc motor with an armature resistance of 0.03 ohms and a field resistance of 41.67 ohms. The motor has compensating windings, so armature reaction can be ignored. Mechanical and core losses may be assumed to be negligible for the purposes of this problem. The motor is assumed to be driving a load with a line current of 126A and an initial speed of 1103 r/min. To simplify the problem, assume that the amount of armature current drawn by the motor remains constant.
(a) If the machine's magnetization curve is as in Example 9.2, what is the motor's speed if the field resistance is raised to 50 ohms?
Example 9.4
The motor in Example 9.3 is now connected separately excited as
shown below. The motor is initially
running with
The Effect of an Open Field Circuit
As the field resistance increased, the speed of the motor increased with it. What would happen if this effect were taken to the extreme, if the field resistance really increased? What would happen if the field circuit were actually opened while the motor is running?
From the previous discussion, the flux in the machine will drop, and EA will drop as well. This would cause a really large increase in the armature current, and the resulting induced torque would be quite a bit higher than the load torque of the motor. Therefore, the motor's speed starts to rise and just keeps going up.
In ordinary shunt dc motors operating with light fields, if the armature reaction effects are severe enough, the effect of speed rising can take place. If the armature reaction on a dc motor is severe, an increase in load can weaken its flux enough to actually cause the motor's speed to rise. However, most loads have torque-speed curves whose torque increases with speed, so the increased speed increases its load, which increases the armature reaction, weakening the flux again. The weaker flux causes a further increase in speed, further increase the load, etc. etc. until the motor overspeeds. This condition is known as runaway.
4. The Permanent-Magnet DC Motor
A permanent magnet dc motor (PMDC) is a dc motor whose poles are made of permanent magnets. PMDC motor offer a number of benefits compared with shunt dc motors in some applications.
Advantage: Since the motors do not require an external field circuit, they do not have the field circuit copper losses. Because no field windings are required, they can be smaller than corresponding shunt dc motors.
Disadvantages
Permanent magnets cannot produce as high flux density as an externally supplied shunt field., so a PMDC motor will have a lower induced torque per ampere of armature current than a shunt motor of the same size. Also, PMDC motors run the risk of demagnetization.
A PMDC motor is basically the same machine as a shunt dc motor, except that the flux of a PMDC motor is fixed. Therefore, it is not possible to control the speed of the PMDC motor by varying the field current or flux. The only methods of speed control available for a PMDC motor are armature voltage control and armature resistance control.
5. The Series DC Motor
A series DC motor is a dc motor whose field windings consist of relatively few turns connected in series with the armature circuit.
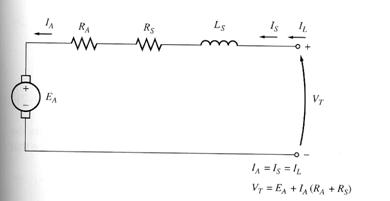
The KVL for this motor is VT = EA + IA (RA + RS)
Induced Torque in a Series DC Motor
The basic behaviour of a series dc motor is due to the fact that the flux is directly proportional to the armature current, at least until saturation is reached. As the load on the motor increases, its flux increases too. As seen earlier, an increase in flux in the motor causes a decrease in its speed. The result is that a series dc motor has a sharply drooping torque-speed characteristic.
The induced torque is t
The flux in this machine is directly proportional to its armature current (at least until metal saturates). Therefore, the flux in the machine can be given by cwhere c is a constant of proportionality. Thus,
t
Series dc motors are therefore used in applications requiring very high torques. Example: starter motors in cars, elevator motors, tractor motors etc.
The Terminal Characteristic of a Series DC Motor
The assumption of a linear magnetization curve implies that the flux in the motor will be given by cThis equation will be used to derive the torque-speed characteristic curve for the series motor.
Derivation of the torque-speed characteristic:
1. VT = EA + IA (RA + RS)
![]()
2.
3. Also, EA = K, thus substituting this in the KVL gives:
![]()
If the flux can be eliminated from this
expression, it will directly relate the torque of a motor to its speed. Notice that IA = c
and t
![]()
Substituting the flux equation into equation in part 3, results in:
The
torque-speed characteristic of a series dc motor
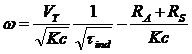
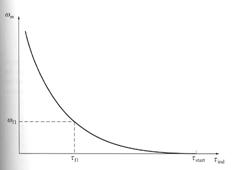
Speed Control of Series DC Motors.
Unlike with the shunt dc motor, there is only one efficient way to change the speed of a series dc motor. That method is to change the terminal voltage of the motor. If terminal voltage is increased, the speed will increase for any given torque.
The Compounded DC Motor
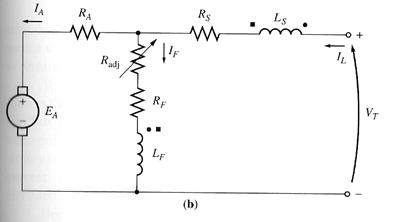
A compounded dc motor is a motor with both a shunt and a series field. This is shown below:
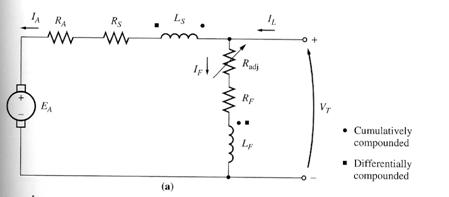
The equivalent
circuit of compounded dc motor: (a) long-shunt
connection. (b)
short-shunt connection.
The KVL for a compounded dc motor is:
VT = EA + IA (RA + RS)
and the currents are:
IA = IL - IF
IF = VT/RF
The net mmf and the effective shunt field current are:
Fnet = FF ± FSE - FAR
IF* = IF ± (NSE/NF) IA - FAR/NF
+ve sign associated with a cumulatively compounded motor
-ve sign associated with a differentially compounded motor
The Torque-Speed Characteristic of a Cumulatively Compounded DC Motor (CC)
There is a component of flux which is constant and another component which is proportional to its armature current (and thus to its load). Thus, CC motor has a higher starting torque than a shunt motor (whose flux is constant) but a lower starting torque than a series motor (whose entire flux is proportional to armature current).
The CC motor combines the best features of both the shunt and series motors. Like a series motor, it has extra torque for starting; like a shunt, it does not overspeed at no load.
At light loads, the series field has a very small effect, so the motor behaves approximately as a shunt dc motor. As the load gets very large, the series flux becomes quite important and the torque-speed curve begins to look like a series motor's characteristic.
A comparison of the torque-speed characteristics of each of these types of machines is shown below:
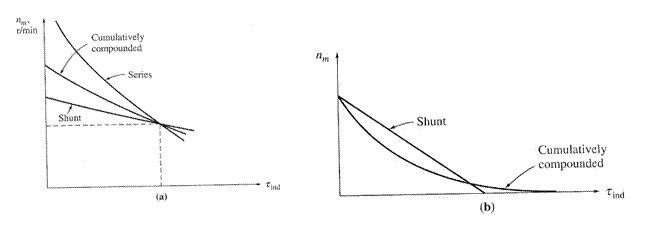
The torque-speed characteristic of a cumulatively compounded dc
motor compared to series and shunt motors with the same full-load rating. The torque-speed characteristic of a cumulatively compounded dc
motor compared to a shunt motor with the same no-load speed.
The Torque-Speed Characteristic of a Differentially Compounded DC Motor
In a differentially compounded dc motor, the shunt mmf and series
mmf subtract from each other. This means
that as the load on the motor increases, IA increases and the flux
in the motor decreases. But as the flux
decreases, the speed of the motor increases. This speed increase causes another increase in load, which further
increases
This instability is much worse than that of a shunt motor with armature reaction. It is so bad that a differentially compounded motor is unsuitable for any application.
Differentially compounded motor is also impossible to start. At starting conditions, the armature current and the series field current are very high. Since the series flux subtracts from the shunt flux, the series field can actually reverse the magnetic polarity of the machine's poles. The motor will typically remain still or turn slowly in the wrong direction while burning up, because of the excessive armature current. When this type of motor is to be started, its series field must be short-circuited, so that it behaves as an ordinary shunt motor during the starting period.
Speed Control in the Cumulatively Compounded DC Motor
Same as for a shunt motor.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||