| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Poezii
|
|
Qdidactic » didactica & scoala » literatura » poezii Poeme geometrice |
Poeme geometrice
|
Punct divin Fiind dat triunghiul care are trei laturi egale Deci e din categoria celor echilaterale Si considerand oricare punct pe cercul circumscris Vom descoperi o lege cu un caracter precis Caci unind cele trei varfuri cu-acest punct, care e cheia, Vom gasi doua distante cu suma egala cu-a treia. Falsul ecuator Voi presupune ca avem O ata lunga pe mosor, Ce-ntrece numai cu un metru Lungimea de ecuator. Si desfacand in minte ata, Incerc perfect sa inconjor, Cu multa truda si migala, Pamantul la Ecuator. Atunci apare cu temei Un semn de intrebare-n fata: Pisica mea cea dragalasa Poate sa treaca pe sub ata? Secrete diagonale Desenati cu un creion un poligon Numarati ale sale laturi si diagonale Demonstrati o regula generala Si aflati o formula universala. Postludiu bisector 'Geometrul adesea adanc se concentreaza' Dante - Divina Comedie Oricare-ar fi doua laturi ce-apartin unui triunghi Se unesc, precum se stie, intr-un punct formand un unghi Si de-aicea se desprinde o dreapta despartitoare Despre care stim cu totii ca se cheama bisectoare Si avand aceste date, fara orice alte sfaturi Singuri veti afla o lege despre cele doua laturi, Caci de doua ori raportul cu produsul lor si suma E, fata de bisectoare, mai mare intotdeauna. Planeta strapunsa 'Cum as putea oare sa-i cer Sa numere ce este-n cer?' L.F.Magnitchi - Aritmetica, 1703 O planeta, Nu stiu dupa care reteta, A fost strapunsa De o racheta Nu stiu cum pe acolo ajunsa. Si de atunci acest sferoid Desi foarte solid A ramas cu o gaura Perfect cilindrica De la un capat la altul Lasata de bolid Care In practica Masoara, Se pare, O subunitate galactica Pe generatoare. Puteti calcula, oare, Indata, Ce volum are
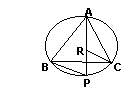
Aceasta planeta ciudata? Duel diagonal 'Doua paralele una langa alta Tot fugeau in zare' M.Cantor - Intalnirea paralelelor Un trapez isoscel desenez cat mai fidel si constat pe hartie ca linia sa mijlocie e egala in lungime cu a lui inaltime iar acum demonstrez ca un astfel de trapez are ale sale diagonale strict perpendiculare. Comensurabilitate 'Nu merita numele de om, acela care nu stie ca diagonala patratului este incomensurabila cu latura sa' Platon Un teren dreptunghiular de arie cat un ar, are, masurat cu metrul, cincizeci si opt in perimetru, dar, daca-l masori la scoala, cat are-n diagonala? Interior Spune, daca poti sa afli, octogonul regulat Care-ncape cel mai bine intre laturi de patrat? Ecou pitagoreic 'De nu-ntelegi stiinta mea sa intri nu-i permis' Pitagora Intr-un triunghi oarecare, una din laturi la patrat face exact cat suma de patrate a celorlalte doua laturi alaturate plus (atunci cand unghiul opus este obtuz) sau minus (atunci cand unghiul amintit e ascutit) dublul produs al uneia dintre aceste laturi cu proiectia celeilalte pe ea. Suprafete 'Nimeni sa nu intre in casa mea daca nu e geometru' Platon Unind mijloace de laturi La orice trapez Am vazut ca pot sa aflu Sau sa calculez, Cu destula usurinta Si fara mister, Aria celui ce este Nou patrulater. POEME GEOMETRICE – RASPUNSURI Punct divin Fie triunghiul echilateral ABC inscris in cerc (vezi figura), iar pe acest cerc consideram un punct oarecare P. Din acest punct construim segmentele PA, PB, PC despre care trebuie sa demonstram relatia enuntata. Pe segmentul AP consideram un punct R cu prprietatea ca segmentele PR si PC sunt cungruente, deci triunghiul PRC este isoscel. Insa unghiul <APC este de 60 , si subintinde acelasi arc de cerc ca si unghiul <ABC, ceea ce inseamna ca triunghiul PRC este echilateral. Acum vom observa ca triunghiurile ARC si BPC sunt congruente, intrucat AB = BC, RC = PC iar unghiurile <ARC si <BPC au fiecare cate 120 Ca urmare, rezulta ca segmentele AR si BP sunt congruente, de unde se poate vedea ca segmentul AP este egal cu suma segmentelor BP si PC.
|
||||
|
Falsul ecuator Fie r raza Pamantului la ecuator. Lungimea ecuatorului este 2r, masurata in metri, iar lungimea atei va fi 2r+1=2R, masurata tot in metri. Atunci 2R-2r = 1, deci R-r = 0,5. Rezulta ca distanta dintre cele doua cercuri concentrice (diferenta dintre razele acestora), este 0,5, adica ceva mai mult de 15 centimetri. Asadar, se poate accepta faptul ca o pisica se poate strecura pe sub aceasta ata. |
||||
|
Secrete diagonale Fie P , P , . . . , Pn cele n varfuri ale unui poligon cu n laturi. Daca pornim cu constructia diagonalelor incepand cu punctul P , atunci din acest punct si din urmatorul P vom putea construi cate n-3 diagonale. Incepand insa cu punctul P si urmatoarele, numarul diagonalelor ce pot fi construite scade cu cate o unitate pentru fiecare punct, pana in punctul Pn-2 cand se va putea duce doar o singura diagonala iar din punctele Pn-1 si Pn nu se va mai putea duce nici o diagonala. Prin urmare, numarul total de diagonale pentru un poligon cu n laturi va fi : N = 1 + 2 + . . . + (n-3) + (n-3) = n(n-3)/2. |
||||
|
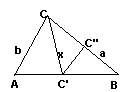
Postludiu bisector In triunghiul ABC consideram bisectoarea CC' si ducem paralela C'C'' la latura AC. Notam BC = a si AC = b iar bisectoarea CC' o notam cu x (vezi figura). Din asemanarea triunghiurilor AC'C'' si ABC gasim ca DC''/BC = C'C''/AC sau (a-CC'')/a = C'C''/b.
Din triunghiul CC'C'' care este isoscel avem ca CC'' = C'C'', de unde gasim ca CC'' = ab/(a+b). Dar in tringhiul CC'C'' avem si x < 2CC''. Asadar, se gaseste inegalitatea din enuntul problemei, adica x < 2ab/(a+b). |
||||
|
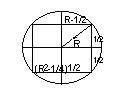
Planeta strapunsa Fie R raza sferei (planetei). Din figura de mai jos deducem ca raza gaurii cilindrice va fi radacina patrata din R -1/4, iar inaltimea calotelor sferice va fi de R-1/2. Pentru a determina volumul corpului ramas prin indepartarea gaurii cilindrice si a celor doua calote sferice vom scadea volumul acestora din volumul planetei initiale.
Volumul planetei este 4R /3. Volumul calotei se obtine din formula urmatoare: 4h(3r +h )/6, unde h reprezinta inaltimea iar r este raza. Asadar, volumul calotei sferice este p(4R -3R +1/4)/6, iar volumul cilindrului este p(R Prin diferenta se obtine volumul planetei gaurite, adica /6 u.g. Observatie : Prin u.g. s-a notat unitatea de masura care in problema apare sub denumirea de 'unitate galactica'. |
||||
|
Duel diagonal In figura de mai jos se considera AB = a si DC = b. Atunci MN = (a + b)/2 = DD' = CC' (ipoteza). Cum AD' = BC' = (a-b)/2, rezulta ca AC' = BD' = h+(a-b)/2. Asta inseamna ca triunghiurile ACC' si BDD' sunt dreptunghice isoscele si folosind unghiurile lor de 450, gasim imediat ca AC este perpendiculara peBD.
|
||||
|
Comensurabilitate Daca d este diagonala, iar x si y sunt laturile dreptunghiului atunci, din datele problemei, deducem urmatoarele relatii: xy = 100 Dar d2 = x2
+ y2 = (x+y) 2 - 2xy = 641. |
||||
|
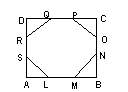
Interior Se considera un patrat de latura 1. Octogonul regulat de arie maxima inscris in patrat este cel care se poate vedea in figura de mai jos.
Notam cu x latura acestui octogon si rezulta ca AL = MB = (1-x)/2. Cum triunghiurile SAL, MBN, OCP, QDR sunt dreptunghice isoscele, avem, aplicand teorema lui Pitagora, ca 2((1-x)/2) = x , ecuatie din care gasim singura solutie valabila: x = V2 - 1. |
||||
|
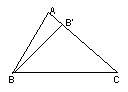
Ecou pitagoreic Avem de-a face cu faimoasa teorema a lui Pitagora sub forma ei generalizata.
Consideram cazul triunghiului ABC cu unghiul <A ascutit. Fie BB' proiectia punctului B pe latura AC. Folosind teorema lui Pitagora in triunghiurile dreptunghice BCB' si BAB' gasim ca: BC = AB + B'C - AB' = AB + (AC-AB') = AB + AC - 2AB'.AC. In mod analog se rezolva si cazul unghiului obtuz. |
||||
|
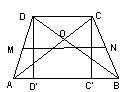
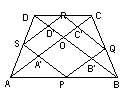
Suprafete In figura de mai jos punctele P, Q, R, S sunt mijloacele laturilor trapezului ABCD. Construim diagonalele AC si BD si fie O punctul lor de intersectie. Aria patrulaterului OA'PB' este jumatatea ariei triunghiului OAB (segmentele A'P, B'P si A'B' sunt linii mijlocii).
In mod analog, ariile patrulaterelor OB'QC', OC'RD' si OD'SA' sunt egale fiecare cu jumatati de arii ale triunghiurile OBC, OCD si respectiv, ODA. In consecinta, prin insumare, aria patrulaterului PSQR este o jumatate din aria trapezului dat. |
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Lucrari pe aceeasi tema
| |||
|
| |||
|
|||
|
|
|||