
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Anova in seriile de experiente monofactoriale |
Anova in seriile de experiente monofactoriale
Curs
Prin serii de experiente se intelege executarea aceleiasi experiente elementare concomitent in mai multe localitati, succesiv in mai multi ani sau succesiv in mai multe localitati si mai multi ani. Necesitatea unor astfel de experiente este impusa de faptul ca anumite caracteristici geodezice ale terenurilor destinate exploatatiilor agricole, unor constructii industraiale sau civile etc. variaza atat in spatiu (de la o locatie la alta) cat si in timp (de la un an la altul). Pentru exemplificare este suficient sa amintim ca adancimea apei freatice variaza in mod simtitor, in acelas loc, de la un an la altul iar gradul de alunecare a terenului, la o anumita adancime, este sensibil diferit de la o locatie la alta.
Analiza variabilitatii monofactoriale intr-o serie de experiente seamana destul de mult cu ceea ce s-a spus la variabilitatea monofactoriala in experiente elementare, obisnuite. Diferenta consta in faptul ca, in seriile de experiente, alaturi de variabilitatea datorata deosebirilor dintre variante, de cea datorata blocurilor si/sau coloanelor si de cea datorata erorilor, se manifesta si o variabilitate datorata localitatilor/anilor de experiemntare precum si una datorata interactiunii dintre variante si ani/localitati. Matematic, in termeni de varianta, acest model de variabilitate totala poate fi reprezentat astfel:
![]()
Formula de mai ne arata ca, de fapt, seria de experiente monofactoriale transforma acest tip de experiente intr-una bifactoriala, localitatea sau anul actionand ca un factor experimental suplimentar introdus de cercetator in scopul sporirii preciziei rezultatelor obtinute. In cazul in care seria de experiente monofactoriale este executata atat in locatii diferite cat si in ani diferiti, se ajunge, de fapt, la o experienta trifactoriala de tipul variante × localitati × ani (V × L × A.). Pentru astfel de serii de experiente, formula de mai sus devine:
![]()
Pentru necesitatile prezentului curs, sa se considere urmatorul exemplu: Se da umiditatea solului (U%), determinata in trei repetitii, pe sase sisteme de inlaturare a excesului de umiditate de pe terenurile agricole, la adancimea de 40 cm. Toate sistemele sunt amplasate in aceeasi localitate, pe acelasi tip de sol si se afla in al 5-lea, respectiv al 6-lea an de exploatare. Sa se arate care din sistemele incercate au cea mai mare/cea mai mica eficienta in eliminarea excesului de umiditate.
Tabelul 11.1.
Rezultatele masuratorilor de umiditate a solului (U%), la adancimea
de 40 cm, in doi ani consecutivi, pe sase sisteme de inlatutrare a excesului de umiditate
|
|
An 1 |
Suma B |
An 2 |
Suma B |
||||||||||||||
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
B2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
B3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Rezulta (tabel 11.1) ca experienta, in cei doi ani de experimentare, a fost amplasata in blocuri randomizate, in trei repetitii. Se poate deci scrie: v = 6; n = 3; a = 2; N= 36.
In scopul continuarii calculelor necesitate de analiza variantei, este necesara asezarea acestor date in ordine sistematica, pe variante si repetitii. Tehnica de executare a acestei operatiuni a fost discutata detaliat la analiza variantei monofactoriale in asezari obligate, asa ca ea nu va mai fi repetata aici ci doar prezentata in tabelul 11.2.
Tabelul 11.2
Aszarea sistematica a rezultatelor, pe variante si repetitii
|
Metoda de eliminare a excesului de umiditate |
LOCALITATEA 1, AN 1 |
LOCALITATEA 1, AN |
∑VT |
Media varian- tei |
||||||
|
I |
II |
III |
∑V-1 |
I |
II |
III |
∑V-2 |
|||
|
1.Desecare biologica.,Mt. |
|
|
|
|
|
|
|
|
|
|
|
2.Scurgere de suprafata |
|
|
|
|
|
|
|
|
|
|
|
3.Canale deschise |
|
|
|
|
|
|
|
|
|
|
|
4.Colmatarea terenului |
|
|
|
|
|
|
|
|
|
|
|
5.Drenaje ceramice |
|
|
|
|
|
|
|
|
|
|
|
6.Drenaje frontale |
|
|
|
|
|
|
|
|
|
|
|
∑B |
|
|
|
|
|
|
|
|
|
|
Si in acest caz, este necesar sa reamintim cheile de verificare a corectitudinii transcrierii datelor: sumele blocurilor, din fiecare an, trebuie sa fie identice cu cele calculate in tabelul 11.1; apoi, ∑Ban1 + ∑Ban2 = ∑x (in cazul exemplificat, 547,7 + 525,8 = 1073,5).
Etapele analizei variantei se desfasoara, pana la un punct, in mod asemanator celui descris la variabilitatea bifactoriala.
a). Calcularea scazatorului
(termenului de corectie) : ![]()
![]() =
= ![]() =
=
b). Calcularea SPA. Datele tabelului 11.2. evidentiaza trei categorii principale de efecte ale variantelor, ale anilor de experimentare si ale interactiunii V × A, si anume;
- valorile individuale ale coloanelor ∑V-1 si ∑V-2 reprezinta efectul combinatiei
variantelor, al anilor experimentali si al interactiunii V × A;
- valorile individuale ale randului ∑B reprezinta efectul combinatiei repetitiilor si al anilor experimentali A × R;
- suma valorile individuale ale coloanelor ∑V-1 si ∑V-2 reprezinta efectul anilor experimentali .
Se poate, deci, scrie:
SPAT = Sx2 - C = 35,22 +.. . + 25,92 + 32,32 + . .+ 32,12 - 32011,2 = 337,82
SPAcomb R × A = ![]()
SPAcombV×A =![]()
SPAA = ![]()
SPAR = SPA combR×A - SPAA = 49,2 - 13,32 = 35,88
SPAV = ![]()
SPAV×A = SPA combV×A - (SPAA + SPAV)= 234,63 - 13,32 - 144,0 = 77,30
SPAE = SPAT-(SPAR+SPAA+SPAV+SPA V×A) = 337,82-35,88-13,32-144,0-77,3=67,31
c). Calcularea gradelor de libertate se face dupa formula cunoscuta : GL = n - 1. In cazul exemplului analizat, GLT=35, GLR=(n1-1)+(n2-1) =4, GLA=1, GLV= 5, GLA V= 5 iar GLE=35-15 = 20.
d) Intocmirea tabelului variantelor. La
acest tip de experiente, tabelul variantelor va trebui sa
cuprinda SPA si GL pentru toate elementele calculate anterior, iar
proba F se va calcula atat fata de varianta erorii (![]() ) cat si fata de varianta
interactiunii V × A (
) cat si fata de varianta
interactiunii V × A (![]() ).
).
Datele din tabelul variantelor arata ca variabilitatea totala a datelor experimentale este, cu adevarat, datorata deosebirilor dintre variante si mult mai putin erorilor experimentale. Interactiunea V × A pare a nu avea o influenta semnificativa asupra variabilitatii datelor experimentale.
Tabelul 11.3.
Tabelul variantelor
pentru seria de experiente monofactoriala, v=6, n=3; a=2
|
Cauza variabilitatii |
SP |
GL |
s˛ |
PROBA F |
|||
|
Fata de |
Fata de |
||||||
|
Totala |
|
|
|
|
|
|
|
|
Blocuri |
|
|
|
|
|
|
|
|
Ani (loc) |
|
|
|
|
|
|
|
|
Variante |
|
|
|
8,56>2,71;4,10 |
1,86<5,05 |
||
|
V x A |
|
|
|
4,59>2,71;4,10 |
|
|
|
|
Eroare |
|
|
|
|
|
|
|
e). Calcularea abaterii standard a diferentei (![]() ) se face atat pentru eroare (sd(e)) cat si pentru
interactiunea V × A (sd(i))
) se face atat pentru eroare (sd(e)) cat si pentru
interactiunea V × A (sd(i))
![]() =
= 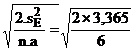 =1,06 %U
=1,06 %U ![]() =
= 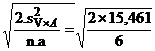 = 2,27 %U
= 2,27 %U
f). Calcularea DL se face dupa formula cunoscuta: DL
= ![]() × t . Valorile t, pentru P5%, P1%,
P0,1% si GLE= 20 sunt (tabel anexa 4): 2,09; 2,84 si 3,85. Vor trebui calculate doua seturi de
valori DL : pentru stabilirea semnificatiei diferentelor intre variante
pe baza
× t . Valorile t, pentru P5%, P1%,
P0,1% si GLE= 20 sunt (tabel anexa 4): 2,09; 2,84 si 3,85. Vor trebui calculate doua seturi de
valori DL : pentru stabilirea semnificatiei diferentelor intre variante
pe baza ![]() si pentru stabilirea
semnificatiei diferentelor intre variante pe baza
si pentru stabilirea
semnificatiei diferentelor intre variante pe baza ![]() . Pentru
usurarea calculelor, este recomandabil ca acest lucru sa fie realizat
sub forma tabelara.
. Pentru
usurarea calculelor, este recomandabil ca acest lucru sa fie realizat
sub forma tabelara.
Tabelul11.4.
Calcularea DL (%U) pentru pentru seria
de experiente monofactoriala, v=6, n=3; a=2
|
|
Pe baza |
Pe baza |
|
DL5% |
|
|
|
DL1% |
|
|
|
DL0,1% |
|
|
g). Intocmirea tabelului de sinteza a rezultatelor
experimentale. Procedeul este foarte asemanator cu cel folosit pentru
experientele monofactoriale elementare cu deosebirea ca, in seriile
de experiente, se va testa semnificatia diferentelor fata
de martor si pe baza DL calculate
cu ajutorul ![]() .
.
Tabelul 11.5
Sinteza rezultatelor experimentale
pentru seria de experiente monofactoriala, v=6, n=3; a=
|
Varianta |
Umid. sol % |
± d. %umid. |
Semnificatia diferentei |
|
|
Fata de |
Fata de |
|||
|
1.Desecare biolog.,Mt. |
|
|
|
|
|
2.Scurgere de supraf. |
|
|
|
|
|
3.Canale deschise |
|
|
ooo |
o |
|
4.Colmatarea teren. |
|
|
|
|
|
5.Drenaje ceramice |
|
|
|
|
|
6.Drenaje frontale |
|
|
oo |
|
DL 5% = 2,2 4,6
DL 5% = 3,0 6,4
DL 5% = 4,1 8,7
h). Interpretarea rezultatelor experimentale.
Cea mai drastica reducere a umiditatii solului, la adancimea de 40 cm, se realizeaza prin utilizarea canalelor deschise si a drenajelor frontale in scopul inlaturarii excesului de umiditate din sol cauzat de precipitatii.Umiditatea solului, in aceste doua variante de drenaj, a fost distinct si foarte semnificativ mai mica decat in varianta martor (desecare biologica). Scurgerea de suprafata, colmatarea terenului si drenajele ceramice au avut cele mai slabe efecte de reducere a umiditatii solului, identice cu cele al martorului. Canalele deschise au tendinta de a ramane constant superioare in eliminarea excesului de umiditate indiferent de fluctuatiile regimului pluviometric de la un an la altul.
Dintre metodele testate, de departe cea mai eficienta s-a dovedit desecarea prin canale deschise care, indiferent de conditiile anului experimental (cantitatea de precipitatii cazuta) a inregistrat o reducere semnificativa a umiditatii solului la adancimea de 40 cm.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








