
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Momentele unei variabile aleatoare discrete |
Momentele unei variabile aleatoare discrete
Momentele unei variabile aleatoare discrete
Se considera doua variabile aleatoare ![]() si
si ![]() si se presupune ca
si se presupune ca![]() poate lua valorile
poate lua valorile ![]() , iar
, iar ![]() poate lua valorile
poate lua valorile ![]() Pentru
fiecare pereche
Pentru
fiecare pereche ![]() , fie
, fie ![]() probabilitatea ca
probabilitatea ca ![]() sa ia valoarea
sa ia valoarea ![]() si
si ![]() sa ia valoarea
sa ia valoarea ![]() , adica:
, adica:
![]()
![]()
![]()
DEFINITIE Probabilitatile
![]()
![]()
![]() constituie repartitia
comuna a variabilelor aleatoare
constituie repartitia
comuna a variabilelor aleatoare ![]() ,
, ![]() .
.
DEFINITIE
Variabilele aleatoare ![]() si
si ![]() sunt independente, daca
pentru orice
sunt independente, daca
pentru orice ![]() ,
, ![]() si orice
si orice
![]()
![]() are loc:
are loc:
![]() .
.
Se considera acum mai mult de doua
variabile aleatoare. Fie ![]() ,
, ![]() variabile aleatoare,
unde variabila aleatoare
variabile aleatoare,
unde variabila aleatoare ![]() ia valorile
ia valorile ![]() ,
, ![]() .
.
DEFINITIE Probabilitatile :
![]()
constituie repartitia comuna a
variabilelor aleatoare ![]()
DEFINITIE
Variabilele aleatoare ![]() sunt independente,
daca pentru orice
sunt independente,
daca pentru orice ![]()
![]()
![]()
![]()
DEFINITIE Variabilele aleatoare ![]() [1] sunt
independente, daca orice numar finit de variabile aleatoare din acest sir sunt
independente.
[1] sunt
independente, daca orice numar finit de variabile aleatoare din acest sir sunt
independente.
Introducem acum o caracteristica numerica foarte importanta, asociata unei variabile aleatoare.
DEFINITIE Numarul
![]()
se numeste valoarea medie
a variabilei aleatoare ![]()
EXEMPLU In experimentul cu zarul :
![]()
DEFINITIE Fie ![]() un numar intreg,
un numar intreg, ![]() . Numarul
. Numarul
![]()
se numeste moment de
ordinul ![]() al variabilei aleatoare
al variabilei aleatoare ![]()
OBSERVATIE Momentul de ordinul ![]() este valoarea medie.
este valoarea medie.
DEFINITIE Numarul
![]()
se numeste dispersia variabilei
aleatoare ![]()
Cu ajutorul acestor notiuni introduse, se pot demonstra o serie de proprietati.
PROPRIETATEA 1 Fie ![]() o variabila aleatoare si
o variabila aleatoare si
![]() un numar intreg,
un numar intreg, ![]() . Atunci
. Atunci
![]()
Demonstratie Fie variabila aleatoare ![]() cu repartitia
cu repartitia
![]()
Atunci variabila aleatoare ![]() va avea evident repartitia :
va avea evident repartitia :

cu alte cuvinte, valorile ![]() si
si ![]() au aceeasi
probabilitate
au aceeasi
probabilitate ![]() ,
,
![]() si deci
si deci
![]() (
(![]() )
)
Din proprietatea anterioara se deduce imediat:
PROPRIETATEA 2 Fie ![]() o variabila aleatoare
care poate lua o singura valoare
o variabila aleatoare
care poate lua o singura valoare ![]() cu probabilitatea
cu probabilitatea ![]() (adica
(adica![]() ). Atunci:
). Atunci:
![]() .
.
PROPRIETATEA 3 Fie ![]() o variabila aleatoare si
o variabila aleatoare si
![]() un numar real. Atunci:
un numar real. Atunci:
![]() .
.
|
Demonstratie. Fie variabila
aleatoare ![]() cu valorile
cu valorile ![]() , avand probabilitatile
, avand probabilitatile ![]() si fie
si fie ![]() . Aceasta noua variabila
aleatoare ia valorile
. Aceasta noua variabila
aleatoare ia valorile ![]() cu aceleasi probabilitati
cu aceleasi probabilitati ![]() si deci:
si deci:
![]() (
(![]() )
)
PROPRIETATEA 4 Fie ![]() variabile aleatoare
variabile aleatoare ![]() . Atunci valoarea medie a sumei acestor variabile
aleatoare este egala cu suma valorilor medii, adica:
. Atunci valoarea medie a sumei acestor variabile
aleatoare este egala cu suma valorilor medii, adica:
![]() .
.
Demonstratie. Fie mai intai numai doua variabile aleatoare ![]() si
si ![]() . Se presupune ca variabila
aleatoare
. Se presupune ca variabila
aleatoare ![]() ia valorile
ia valorile ![]() cu probabilitatile
cu probabilitatile ![]() , iar variabila aleatoare
, iar variabila aleatoare ![]() ia valorile
ia valorile ![]() cu probabilitatile
cu probabilitatile ![]() . De asemenea fie :
. De asemenea fie :
![]() ,
, ![]() ,
, ![]() .
.
Fie ![]() ; aceasta noua variabila aleatoare ia valoarea
; aceasta noua variabila aleatoare ia valoarea ![]() cu probabilitatea
cu probabilitatea ![]() ,
, ![]() ,
, ![]() . Prin urmare :
. Prin urmare :
![]()
![]()
![]()
Suma ![]() , este suma probabilitatilor
tuturor evenimentelor de forma
, este suma probabilitatilor
tuturor evenimentelor de forma ![]() , unde indicele
, unde indicele ![]() este acelasi pentru toti termenii sumei, iar
indicele
este acelasi pentru toti termenii sumei, iar
indicele ![]() variaza de la un termen la altul, parcurgand
toate valorile de la
variaza de la un termen la altul, parcurgand
toate valorile de la ![]() la
la ![]() . Deoarece evenimentele
. Deoarece evenimentele ![]() pentru indici
pentru indici ![]() diferiti sunt incompatibile doua cate doua,
suma
diferiti sunt incompatibile doua cate doua,
suma ![]() este probabilitatea producerii
unui eveniment oarecare din cele
este probabilitatea producerii
unui eveniment oarecare din cele ![]() evenimente
evenimente ![]() ,
, ![]() . Dar, a spune ca s-a produs un eveniment oarecare din evenimentele
. Dar, a spune ca s-a produs un eveniment oarecare din evenimentele
![]() ,
, ![]() , este echivalent cu a spune ca s-a produs evenimentul
, este echivalent cu a spune ca s-a produs evenimentul ![]() . Intr-adevar, daca s-a produs
unul din evenimentele
. Intr-adevar, daca s-a produs
unul din evenimentele ![]() ,
, ![]() , este evident ca s-a produs si evenimentul
, este evident ca s-a produs si evenimentul ![]() ; reciproc, daca s-a produs
evenimentul
; reciproc, daca s-a produs
evenimentul ![]() , atunci intrucat variabila
aleatoare
, atunci intrucat variabila
aleatoare ![]() ia neaparat una din valorile sale posibile
ia neaparat una din valorile sale posibile ![]() , trebuie sa se produca si un
eveniment oarecare din evenimentele
, trebuie sa se produca si un
eveniment oarecare din evenimentele ![]() ,
, ![]() . Asadar,
. Asadar, ![]() fiind probabilitatea producerii unui eveniment
oarecare din evenimentele
fiind probabilitatea producerii unui eveniment
oarecare din evenimentele ![]() ,
, ![]() , este egala cu probabilitatea evenimentului
, este egala cu probabilitatea evenimentului ![]() , adica
, adica
![]()
![]() .
.
In mod analog se deduce:
![]()
![]() .
.
Tinand seama de aceste expresii in relatia
![]() , se obtine :
, se obtine :
![]()
![]()
Pentru mai mult de doua variabile aleatoare, se procedeaza prin inductie. Fie
![]()
si se presupune teorema adevarata
pentru ![]() . Atunci :
. Atunci :
![]()
Aplicand proprietatea pentru doua variabile aleatoare, se obtine :
![]()
![]()
![]()
PROPRIETATEA 5 Dispersia unei variabile aleatoare ![]() este data de relatia :
este data de relatia :
![]() .
.
Demonstratie. ![]()
![]() ,
,
daca se tine seama de proprietatea precedenta. Mai departe, aplicand de doua ori proprietatea 1., se obtine :
![]() .
. ![]()
PROPRIETATEA 6 Fie ![]() si
si ![]() doua variabile aleatoare independente. Atunci
valoarea medie a produsului acestor variabile aleatoare este egala cu produsul
valorilor medii, adica :
doua variabile aleatoare independente. Atunci
valoarea medie a produsului acestor variabile aleatoare este egala cu produsul
valorilor medii, adica :
![]()
Demonstratie. Se presupune ca variabila aleatoare ![]() ia valorile
ia valorile ![]() cu probabilitatile
cu probabilitatile ![]() , iar variabila aleatoare
, iar variabila aleatoare ![]() ia valorile
ia valorile ![]() cu probabilitatile
cu probabilitatile ![]() . De asemenea :
. De asemenea :
![]() ,
, ![]() ,
, ![]()
si cum f si g sunt variabile independente:
![]()
![]()
![]()
Fie ![]() ; aceasta noua variabila aleatoare ia valoarea
; aceasta noua variabila aleatoare ia valoarea![]() cu probabilitatea
cu probabilitatea ![]()
![]()
![]() . Prin urmare:
. Prin urmare:
![]()
![]()
![]()
PROPRIETATEA 7 Fie ![]() variabile aleatoare
variabile aleatoare ![]() independente doua cate
cate doua. Atunci dispersia sumei
acestor variabile aleatoare este egala cu suma dispersiilor, adica:
independente doua cate
cate doua. Atunci dispersia sumei
acestor variabile aleatoare este egala cu suma dispersiilor, adica:
![]()
Demonstratie. Din proprietatea 6 se deduce
![]()
![]()
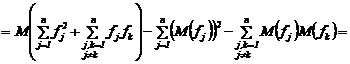
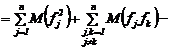
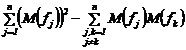
Daca se tine seama de faptul ca
variabilele aleatoare ![]() sunt independente,
atunci din proprietatea 6 rezulta ca cele doua sume duble de mai sus se reduc si
deci :
sunt independente,
atunci din proprietatea 6 rezulta ca cele doua sume duble de mai sus se reduc si
deci :
![]()
![]()
![]() .
.
PROPRIETATEA 8 (Inegalitatea
lui Cebisev) Fie ![]() o variabila aleatoare si
o variabila aleatoare si
![]() un numar pozitiv
oarecare. Atunci
un numar pozitiv
oarecare. Atunci
![]() ,
,
sau
![]()
Demonstratie Fie ![]() o variabila aleatoare
care ia valorile
o variabila aleatoare
care ia valorile ![]() cu probabilitatile
cu probabilitatile ![]() . Dispersia variabilei aleatoare
. Dispersia variabilei aleatoare ![]() este :
este :
![]()
Fie ![]() este un numar
oarecare; daca din suma de mai sus se elimina toti termenii pentru care
este un numar
oarecare; daca din suma de mai sus se elimina toti termenii pentru care ![]() si raman
numai termenii pentru care
si raman
numai termenii pentru care ![]() , suma poate numai sa se
micsoreze, adica
, suma poate numai sa se
micsoreze, adica
![]() .
.
Aceasta suma se
va micsora si mai mult daca in fiecare termen al ei vom inlocui factorul ![]() prin valoarea
inferioara
prin valoarea
inferioara![]() :
:
![]()
Suma din partea dreapta reprezinta suma
probabilitatilor tuturor acelor valori ![]() ale variabilei aleatoare
ale variabilei aleatoare ![]() care se abat de la valoarea medie
care se abat de la valoarea medie ![]() de o parte si de alta cu mai mult de
de o parte si de alta cu mai mult de ![]() ; conform proprietatii de
aditivitate a doua evenimente incompatibile, aceasta este probabilitatea ca
variabila aleatoare
; conform proprietatii de
aditivitate a doua evenimente incompatibile, aceasta este probabilitatea ca
variabila aleatoare ![]() sa ia una din aceste valori. Cu alte cuvinte,
aceasta suma este
sa ia una din aceste valori. Cu alte cuvinte,
aceasta suma este ![]() . Adica :
. Adica :
![]()
ceea ce permite aprecierea probabilitatii
abaterilor mai mari decat un numar ![]() dat
dinainte, cu conditia numai sa fie cunoscuta dispersia
dat
dinainte, cu conditia numai sa fie cunoscuta dispersia ![]() .
.
Cu ajutorul proprietatilor 7 si 8 se poate demonstram urmatorul rezultat foarte important, cunoscut sub numele de legea numerelor mari.
PROPRIETATEA
9 Fie ![]() un sir de variabile
aleatoare independente care au aceeasi repartitie si deci, aceeasi valoare
medie
un sir de variabile
aleatoare independente care au aceeasi repartitie si deci, aceeasi valoare
medie ![]() si aceeasi dispersie
si aceeasi dispersie ![]() . Atunci, pentru orice
. Atunci, pentru orice ![]() si
si
![]() arbitrari,
arbitrari, ![]()
![]() , exista un numar natural
, exista un numar natural ![]() astfel incat indata ce
astfel incat indata ce
![]() , are loc :
, are loc :
![]()
Demonstratie. Din proprietatile 1 si 4, se deduce:
![]()
si deci, aplicand proprietatea 8, se obtine:
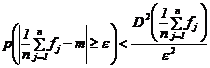
Dar:
![]() ,
,
de unde rezulta:
![]() .
.
Fiind dati
![]()
![]() , se poate determina un numar natural
, se poate determina un numar natural ![]() , care depinde de
, care depinde de ![]() si
si
![]() , astfel incat indata ce
, astfel incat indata ce ![]() , sa rezulte :
, sa rezulte :
Prin urmare :
![]()
Cu alte cuvinte, proprietatea 9 arata ca
daca variabilele aleatoare ![]() sunt independente si daca au aceeasi medie
sunt independente si daca au aceeasi medie ![]() si aceeasi
dispersie
si aceeasi
dispersie ![]() , atunci pentru un
, atunci pentru un ![]() suficient de mare, expresia
suficient de mare, expresia ![]() va diferi oricat de putin de
va diferi oricat de putin de ![]() cu o probabilitate oricat de apropiata de
cu o probabilitate oricat de apropiata de ![]() .
.
Studiul independentei a doua variabile aleatoare se poate realiza si prin intermediul coeficientului de corelatie.
DEFINITIE Se numeste corelatie a doua variabile aleatoare, media produsului abaterilor acestora:
![]() .
.
PROPRIETATE 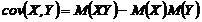
Demonstratie ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
DEFINITIE Se numeste coeficient de corelatie:
![]() .
.
TEOREM{ Corelatia a doua variabile aleatoare independente este nula.
Demonstratie Daca variabilele X, Y sunt
independente, atunci si ![]() , respectiv
, respectiv ![]() sunt independente.
sunt independente.
PROPRIET{TI
1) ![]() ;
;
2) ![]() daca si numai daca intre
variabilele X si Y exista o relatie de legatura liniara.
daca si numai daca intre
variabilele X si Y exista o relatie de legatura liniara.
Demonstratie 1) Fie 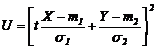 ,
, ![]() .
. ![]() ,
, ![]()
![]() . Calculand media
variabilei aleatoare U, se obtine :
. Calculand media
variabilei aleatoare U, se obtine :
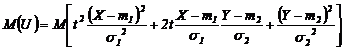
![]()
![]()
![]()
![]()
![]()
![]() .
.
Calculand discriminantul si impunand conditia ca acesta sa fie pozitiv, rezulta proprietatea data.
2) Fie ![]() ,
, ![]() ,
, ![]() .
.
![]()
![]()
![]()
![]()
![]()
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








