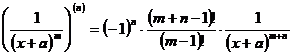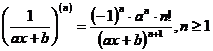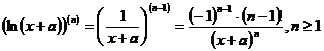| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Derivatele de ordinul n - functii polinomiale |
Derivatele de ordinul n - functii polinomiale
Despre derivatele de ordinul n
Unul dintre cele mai frecvente tipuri de subiecte de admitere din ultimii ani include calculul derivatelor de ordinul n pentru functii apartinand unor tipuri diferite. In materialul de fata, vom prezenta modul in care se determina acestea pentru anumite clase de functii.
Fireste ca in toate
cazurile vom considera o functie 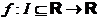 , I fiind un interval, care este de n ori derivabila pe I (de
cele mai multe ori, este chiar indefinit derivabila pe I, adica
derivabila de n ori,
, I fiind un interval, care este de n ori derivabila pe I (de
cele mai multe ori, este chiar indefinit derivabila pe I, adica
derivabila de n ori, ![]() ). In cele mai multe cazuri, nu vom mai
specifica domeniul de definitie/derivabilitate pentru functiile care apar;
aceasta ramane misiunea utilizatorilor.
). In cele mai multe cazuri, nu vom mai
specifica domeniul de definitie/derivabilitate pentru functiile care apar;
aceasta ramane misiunea utilizatorilor.
- Functii polinomiale.
![]()
Avem succesiv:
![]()
![]()
![]()
![]()
Cu
alte cuvinte, dupa n derivari succesive, un polinom de
gradul n se reduce la o
Ex. rezolvat 1 Sa se arate ca
daca polinomul ![]() admite radacina
admite radacina ![]() de multiplicitate
de multiplicitate ![]() , atunci
, atunci ![]() este radacina a primelor (m-1) derivate ale lui f.
este radacina a primelor (m-1) derivate ale lui f.
Solutie. Se scrie f sub forma:
![]() (1.1)
(1.1)
Derivam aceasta relatie si obtinem:
![]()
Daca notam:
![]()
rezulta:
![]() (1.2)
(1.2)
Rationamentul continua cu derivarea succesiva a relatiilor obtinute, rezultand dupa efectuarea unor notatii similare:
![]() (1.3)
(1.3)
.
![]() ceea
ce incheie demonstratia.
ceea
ce incheie demonstratia.
Ex. rezolvat 2 (admitere in clasa a XI-a, 1987) Sa se determine parametrii ![]() astfel incat polinomul
astfel incat polinomul ![]() sa fie divizibil cu
sa fie divizibil cu ![]() .
.
Solutie
Divizibilitatea cu ![]() echivaleaza cu
echivaleaza cu ![]() radacina dubla si deci (conform exercitiului precedent) se
pun conditiile
radacina dubla si deci (conform exercitiului precedent) se
pun conditiile ![]() . Dar:
. Dar:
![]()
Rezolvand sistemul, gasim: ![]() .
.
- Functii rationale.
Trebuie spus de la bun inceput ca nu toate functiile rationale se
deriveaza 'frumos' de n ori. Un bun exemplu este ![]() ; calculul derivatei de ordinul n pentru o astfel de functie
depaseste cadrul programei de liceu.
; calculul derivatei de ordinul n pentru o astfel de functie
depaseste cadrul programei de liceu.
Care sunt
atunci acele functii rationale de care ne vom ocupa? Pai
numai cele de forma ![]() unde
unde ![]() admite numai radacini
reale. In acest caz, putem scrie:
admite numai radacini
reale. In acest caz, putem scrie:
![]() unde
unde
![]() sunt radacinile lui Q.
sunt radacinile lui Q.
Dupa cum se cunoaste (vezi manualul de Analiza de clasa a XII-a), functia f admite o descompunere in elemente simple de forma:
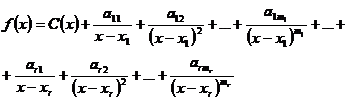
unde C(x) este un polinom (catul impartirii lui P la Q).
2.1 Derivata de ordinul n a functiei ![]() ,
, ![]()
Calculam succesiv:
![]()
![]()
Procedam prin
metoda inductiei matematice: presupunem ca pentru ![]() avem
avem ![]() (* trebuie sa
aratam ca
(* trebuie sa
aratam ca ![]() .
.
Derivam relatia (*) si rezulta:
|
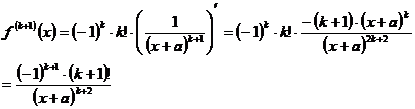
Am obtinut asadar relatia:
|
|
2.2 Aplicatii
A)
Derivata de ordinul n a functiei ![]()
Similar cu rationamentul de mai sus, rezulta ca:
|
|
B)
Derivata de ordinul n a functiei ![]()
Se procedeaza tot prin inductie matematica, obtinand:
|
|
C)
Ex. rezolvat 3. Fie ![]() . Calculati
. Calculati ![]() .
.
Solutie. Descompunem f in elemente simple sub forma:
![]()
Dupa aducerea
la acelasi numitor si identificarea coeficientilor, rezulta ![]() . Deci
. Deci ![]()
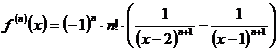 .
.
Functii trigonometrice, exponentiale, logaritmice etc.
3.1 Functia ![]()
Arhicunoscuta de la fizica (descrie ecuatia unei oscilatii armonice fara pierderi de energie). Calculam succesiv:
![]()
![]()
![]()
![]()
Am ajuns la ceva care
seamana cu functia data, numai ca are un factor de amplificare egal cu ![]() . Am putea sa demonstram formule de
genul:
. Am putea sa demonstram formule de
genul:
![]()
numai ca pentru ![]() ar trebui sa stabilim
o alta formula etc. Aceasta lipsa de unitate nu ar fi deloc de natura sa simplifice forma rezultatului final.
ar trebui sa stabilim
o alta formula etc. Aceasta lipsa de unitate nu ar fi deloc de natura sa simplifice forma rezultatului final.
Ne amintim de formulele de reducere la primul cadran, invatate la trigonometrie in clasa a IX-a (speram noi J) si rezulta:
![]()
![]()
![]()
Acum presupunem (pasul
de inductie) ca ![]() si trebuie sa demonstram ca:
si trebuie sa demonstram ca:
![]() .
.
Intr-adevar, ![]() (tinand seama
ca are loc identitatea
(tinand seama
ca are loc identitatea ![]() ):
):
![]() . Rezulta deci:
. Rezulta deci:
|
|
3.2 Functia ![]()
Rezulta in mod imediat prin inductie dupa n ca:
|
|
3.3 Functia ![]() .
.
Avem ![]() si de aici incolo
rezulta ca:
si de aici incolo
rezulta ca:
|
|
Ex. rezolvat 4 (dat la admitere prin 1983 mi se pare). Sa
se demonstreze ca functia ![]() nu este polinomiala.
nu este polinomiala.
Solutie.
Daca functia data ar fi polinomiala de grad ![]() , ar trebui ca
, ar trebui ca ![]() . Dar
. Dar ![]() . Contradictia este evidenta.
. Contradictia este evidenta.
4. Leibniz, meine Liebe .
Fireste ca daca toate functiile carora li
se poate calcula derivata de ordinul n s-ar reduce la
functii de unul din tipurile de mai sus, materialul s-ar termina aici. Exista
insa o celebra formula datorata lui Leibniz (unul din intemeietorii,
alaturi de
![]() (4.1)
(4.1)
OBSERVATIE. In formula de mai sus,![]() .
.
Nu demonstram aici formula lui Leibniz. Probabil ca viitoarele manuale de clasa a XI-a o vor face; cred ca tratatele serioase de Analiza Matematica (cum ar fi cel alcatuit de Miron Nicolescu/M. Dinculeanu/S.Marcus in 1966) cuprind demonstratia acestei formule. In prezentul manual, a figurat ca exercitiu pana cand a fost scoasa pentru a nu obosi inutil mintea greu incarcata a bietilor liceeni. Ciudat insa ca la admiterea in diverse facultati in ultimii ani (in special la ASE), aceasta formula a fost necesara in rezolvarea unor subiecte.
INTREBARE (gen 'Vrei sa fii miliardar?') Cu ce formula din Algebra de clasa a X-a 'aduce' relatia lui Leibniz ?
In fine, nu mai divagam inutil. Continuam prin a prezenta cele doua tipuri majore de exercitii care necesita utilizarea formulei (4.1).
4.1 Derivata de ordinul n a unui produs in care unul din factori se "stinge" dupa un numar de pasi.
Fara indoiala ca ati realizat ca e vorba de produse in care unul din factori este un polinom. In acest caz, din dezvoltarea completa a formulei (4.1) vor ramane un numar relativ redus de termeni. Sa luam un exemplu.
Ex. rezolvat 5 Calculati ![]() , unde
, unde ![]() .
.
Solutie Avem
![]() . Deci:
. Deci:
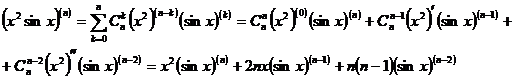
![]()
4.2 Cand nimeni nu cedeaza .
. sau cu alte cuvinte, exista si cazuri
in care nici unul din factori nu se "stinge" dupa ![]() pasi. Un astfel de exemplu este urmatorul:
pasi. Un astfel de exemplu este urmatorul:
Ex. rezolvat. 6. Sa se calculeze derivata de ordinul n a functiei:
![]()
Solutie Avem ![]() unde
unde ![]() si
si ![]() . Dupa cum am vazut in paragrafele anterioare,
. Dupa cum am vazut in paragrafele anterioare, ![]() in vreme ce
in vreme ce ![]() . Conform formulei (4.1)
avem:
. Conform formulei (4.1)
avem:
![]()
![]()
(am despartit
termenul care contine ![]() de restul sumei)
de restul sumei)
![]()
![]()
Interesant, nu-i asa? Probabil ca exercitiul asta la Bac'2001 ar declansa o miscare sociala de amploarea mineriadei din iunie 1990, tinta fiind un anume minister cu sediul pe General Berthelot.
Este foarte probabil ca vom reveni cu o continuare a acestui material, in care vor fi ceva exercitii propuse pe la tot felul de admiteri. Ca sa aveti totusi ceva de lucru, try these:
Exercitii propuse Sa se calculeze ![]() :
:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) 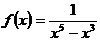
OBSERVATIE IMPORTANTA (for your sake). Nu memorati mecanic formule de genul (2.1) sau (3.2). Este suficient sa stiti sa le deduceti corect; oricum, nu va poate lua mai mult de 3-4 minute. Formula lui Leibniz se poate retine usor daca faceti legatura cu formula de care aminteam din materia clasei a X-a.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||









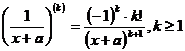 (2.1)
(2.1)