
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Statistica
|
|
Qdidactic » didactica & scoala » matematica » statistica Corelatia statistica - metoda celor mai mici patrate |
Corelatia statistica - metoda celor mai mici patrate
In procesul de cercetare a legaturilor cauzale existente intre fenomenele naturale avem de-a face cu contopirea actiunilor unei multitudini de factori (cauze), dintre care unii esentiali, altii neesentiali, unii pot fi determinati, altii nu. Tocmai de aceea, in cercetarea legaturii reciproce dintre doua fenomene apar dificultati mari deoarece pot sa existe cauze necunoscute. In astfel de situatii este util sa determinam gradul de corelare si apoi sa analizam separat unele din aceste cauze. Cu alte cuvinte, trebuie sa definim relatii posibile intre diferiti factori, evenimente, atribute sau caracteristici care ar putea avea o influenta, cel putin partiala asupra datelor experimentale. In acest mod este posibila stabilirea unui tablou al conditiilor in care se desfasoara un anumit fenomen natural, fapt care duce la modelarea matematica a sa. Astfel de probleme se cerceteaza cu mult succes prin metodele statisticii, unde teoria corelatiei are o pondere insemnata.
Eficienta aplicarii metodei corelatiei depinde de punerea (enuntarea) corecta a problemei in studiu precum si de aplicarea corecta a statisticii matematice.
Caracterul complex al dependentei statistice pune pe primul plan problema identificarii existentei legaturilor. Calculul indicatorilor de corelatie este admis cu conditia stabilirii anticipate a unei legaturi cauzale reale intre fenomenele cercetate. Statistica nu poate sa rezolve o astfel de problema fara ajutorul stiintei din domeniul careia face parte fenomenul studiat. Cu alte cuvinte, specialistul din domeniul respectiv trebuie sa cunoasca temeinic notiunile analizei statistice implicate pentru a da o interpretare corecta a rezultatelor. Pentru a asigura deductii suficient de intemeiate, este necesar includerea in cercetare, daca este posibil, a tuturor factorilor cu actiune esentiala.
In multe procese naturale, pe linga complexa intrepatrundere cu alte fenomene (procese), acestea mai sunt supuse unor evolutii care la prima vedere pot fi considerate probabiliste (aleatoare). De aceea, pentru cunoasterea modului de evolutie probabila in viitor - prognoza unui anumit fenomen - trebuie sa ne bazam pe cunoasterea evolutiei trecute, precum si pe situatia prezenta. Experienta unui mare numar de observatii (probe) au dus la concluzia ca intre diferitele marimi variabile pot exista urmatoarele tipuri de relatii:
a) Relatia de dependenta, Y depinde de X sau invers. O modificare a unei variabile duce la o modificare a celei de-a doua. In cazul unei astfel de relatii s-ar putea aminti existenta relatiei cauzale in care o variabila este cauza, iar cealalta este efectul, cauza fiind un fenomen sau un complex de fenomene care provoaca, genereaza sau determina un alt fenomen - efectul. Operatia logica prin care efectul este dedus din cauza se numeste inferenta cauzala.
b) Relatia de interdependenta, Y depinde de X si X depinde de Y. In acest caz modificarea unei variabile provoaca modificarea celei de-a doua variabile, iar modificarea acesteia din urma are influenta asupra primei variabile.
c) Relatia de tranzitie, X se transforma partial sau total in Y si invers.
d) Corelatia statistica sau covarianta. Pentru X exista intotdeauna Y si invers. Este o relatie reciproca dintre doua variabile, dintre care una in mod logic apeleaza la alta si pe baza analizei datelor experimentale se poate pune in evidenza o asociere intre ele.
e) Relatia stochastica; daca se realizeaza X atunci cu o anumita probabilitate se realizeaza si Y, sau invers.
In cele ce urmeaza vom analiza cu precadere corelatia statistica.
O problema importanta pentru cercetarea corelatiilor este problema determinarii functiei de regresie, care sa exprime relatia cantitativa dintre fenomenul efect si fenomenul cauza. Forma legaturii dintre fenomene si descrierea printr-o ecuatie analitica, pe baza carora se definesc valorile fenomenului efect, in functie numai de factorul sau factorii luati in considerare (cauze).
Pentru ajustarea seriei de valori empirice trebuie sa se aleaga acea ecuatie care oglindeste in modul cel mai corespunzator caracterul legaturii cercetate. De buna alegere a functiei de regresie depinde rezultatele analizei de corelatie, valoarea estimatiilor variabilei dependente. Stabilirea formei legaturii tine seama de natura dependentei fenomenului cercetat (de obicei se reprezinta grafic).
La fenomenele simple, unde cauzele actioneaza separat, relatia dintre fenomenul-efect si fenomenul-cauza se reprezinta sub forma:
y=f(x)
unde x reprezinta cauza, iar y efectul.
La fenomenele complexe, dependenta se exprima sub forma generala:
y = f(x1 , x2 ,, xn)
Fenomenul y este generat de actiunea comuna a factorilor x1 ,x2 ,.., xn (cauze), din care luam insa in calcul numai o parte.
Sa admitem ca am luat in calcul factorul x1. Intrebarea care se pune este urmatoarea: in ce conditii indicatorii corelatiei obtinuti exprima masura reala a influentei variabilei x1 asupra variabilei y? Numai cu conditia ca factorul x1 sa fie hotarator in determinarea lui y, ceilalti fiind nesemnificativi. In cazul in care fenomenul este sub actiunea unui complex de factori esentiali si aceasta este situatia obisnuita, pentru a exprima influenta si gradul de intensitate a legaturilor in raport cu un singur factor trebuie sa eliminam influenta celorlati.
Sa consideram o colectivitate statistica caracterizata prin marimile X si Y. Efectuand o serie de determinari experimentale (sau observatii) asupra acestei colectivitati, putem intocmi tabela datelor respective:
X | x1, x2 , , xn
Y | y1 , y2 , , yn
Repartitia empirica a celor doua variabile se poate afisa grafic, intr-un sistem de axe XOY, unde vom reprezenta punctele de coordonate xi si yi. Un ansamblu de astfel de puncte se numeste camp de corelatie, tabel de corelatie sau nor statistic.
Daca punctele Mi(xi ,yi) sunt distribuite de-a lungul unei fasii, care in general, urmeaza o curba determinata, spunem ca intre marimile respective exista o dependenta functionala. Daca punctele Mi(xi ,yi) nu arata o dependenta functionala stricta, dar exista o tendinta ca valorile lui Y sa depind de cele ale lui X desi nu in mod riguros, intre marimile X si Y exista o corelatie Aceasta poate sa fie liniara (fig. 1) sau neliniara (fig. 2). In cazul cand intre X si Y nu exista nici un fel de dependenta, campul de distributie se va prezenta asemanator cu acela aratat in fig. 3, 4. Cele doua caracteristici sunt independente.
 Figura 2 Distributie neliniara
Figura 2 Distributie neliniara
 Figura 1 Distributie liniara
Figura 1 Distributie liniara
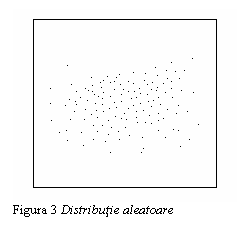
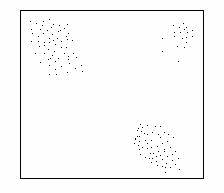 Figura 4 Distributie
grupata
Figura 4 Distributie
grupata
Intr-un caz particular, dependenta corelationara se poate transforma intr-o dependenta functionala, dar cu un anumit grad de certitudine. Apare problema de stabili cantitativ (numeric) in ce masura dependenta corelationala se apropie sau se departeaza de dependenta functionala.
In foarte multe cazuri, din observarea fenomenelor naturale sau a proceselor sociale, fara a cunoaste natura exacta a acestora si nici cauzele prin care este pusa in evidenta o anumita caracteristica, se pot trage concluzii foarte importante prin examinarea corelatiei dintre aceste trasaturi si alte evenimente. In acest mod se poate aprecia existenta unei relatii statistice intre doua sau mai multe variabile, adica, in astfel de cazuri se vorbeste despre corelatii dintre marimile care indica o dependenta reciproca.
In cazul cand se considera numai doua variabile, se pot stabili corelatii simple, iar cand numarul variabilelor este mai mare de doi, avem corelatii multiple.
Din punct de vedere al formei unei relatii statistice, spunem ca ea este directa atunci cand cresterea unei variabile, duce la o crestere a celeilalte variabile, si o denumim inversa cand o crestere a unei variabile duce la o descrestere a celeilalte.
Relatiile statistice definite prin corelatii pot avea aspect liniar sau neliniar; prin urmare vom distinge corelatii liniare si corelatii neliniare sau curbilinii.
In cazul in care sunt implicate mai multe variabile vom avea corelatie partiala cand se considera constante unele variabile si corelatie partiala cand se iau in considerare variatiile tuturor marimilor.
Metoda celor mai mici patrate.
Dependenta functionala a unei variabile y fata de alta variabila x poate fi studiata empiric, pe cale experimentala, efectuindu-se o serie de masuratori asupra variabilei y pentru diferite valori ale lui x. Rezultatele se pot prezenta sub forma de tabel sau grafic.
Problema care se pune in acest caz este de a gasi reprezentarea analitica a dependentei functionale cautate, adica de a alege o formula care sa descrie rezultatele experimentului.
|
Formula se alege dintr-o multime de formule de tip determinat, de exemplu.
y = ax + b , y = ax2 + bx + c , y = aebx + c , y = a + h sin( ωt + φ )
Cu alte cuvinte, problema consta in a determina parametrii a, b, c, ai formulei, in timp ce tipul formulei este cunoscut dinainte ca urmare a unor considerente teoretice sau dupa forma prezentarii grafice a materialului empiric.
Sa notam, la modul general cand avem n parametrii, dependenta functionala prin:
y = f(x; a0 ,a1 ,,an)
Parametrii a0, a1,, an nu se pot determina exact pe baza valorilor empirice y1, y2,,yn ale functiei, deoarece acestea din urma contin erori aleatoare. Este vorba de obtinerea unei estimatii 'suficient de bune'.
Formularea problemei
Daca toate masuratorile valorilor functiei sunt y1, y2,,yn atunci estimatiile parametrilor a0, a1,, an se determina din conditia ca suma patratelor abaterilor valorilor masurate yk de la cele calculate f(xk; a0, a1,, an), adica expresia
![]()
sa ia valoarea minima.
Consideratia formulata se pastreaza si pentru determinarea estimatiilor parametrilor unei functii de mai multe variabile. Adica un efect si doua cauze. De exemplu, pentru functia z de doua variabile x si y, estimatiile parametrilor a , a1,, an se determina din conditia ca expresia:
![]()
sa fie minima.
Aflarea valorilor parametrilor a , a1,, an, care conduc la cea mai mica valoare a functiei
![]()
revine la rezolvarea sistemului de ecuatii
![]()
![]()
![]()
Daca formula empirica depinde liniar de parametrii necunoscuti atunci sistemul de mai sus va fi de asemenea liniar.
Dreapta de regresie.
In cazul cel mai simplu se studiaza numai doua variabile X, Y si se doreste gaairea dependentei:
Y = aX + b
in ipoteza ca X este cauza si Y este efectul.
In urma celor n probe se cunosc datele (xi ,yi), i=1,, n si trebuie sa determinam coeficientii a si b astfel incat suma
![]()
sa fie minima. Se obtine
![]()
![]()
unde sx este dispersia variabilei x, iar sy este dispersia variabilei y.
Marimea
![]()
se mumeste corelatia
variabilelor X si Y. Raportul ![]() se numeste coeficient de
corelatie a variabilelor X, Y si masoara
intensitatea dependentei liniare dintre variabilele X si Y.
se numeste coeficient de
corelatie a variabilelor X, Y si masoara
intensitatea dependentei liniare dintre variabilele X si Y.
In in final se va obtine ecuatia de regresie:
![]()
Aceasta dependenta reprezinta o dreapta numita dreapta de regresie a variabilei Y in raport cu variabila X.
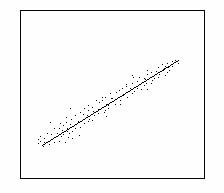
Dreapta de regresie
Observatie. Se poate vorbi si de dependenta variabilei X in functie de Y. Urmand un calcul asemanator se ajunge la dreapta de regresie a variabilei X in raport cu Y:
![]()
Se observa
ca cele doua drepte de regresie coincid daca si numai
daca![]() .
.
Observatii
1. Trebuie sa facem observatia ca, indiferent de gradul de imprastiere al punctelor, intotdeauna se poate gasi o dreapta de regresie, dar in cazul unei dispersii mari aceasta devine inutila. De aceea un studiu preliminar a distributiei punctelor in plan sau spatiu se impune cu necesitate.
2. Coeficientul de corelatie este o marime foarte importanta in cadrul regresiei liniare. El masoara gradul de dependenta liniara intre cauza si efect si are o valoare cuprinsa intre –1 si 1. Apropierea de 1 implica o dependenta liniara puternica intre marimi, iar apropierea de zero indica o lipsa a corelatiei. Valorile negative semnifica o corelatie inversa.
EXEMPLE
In cele ce urmeaza vom lua doua exemple. In primul exemplu vom determina o dreapta de regresie, corespunzatoare debitului si al pH-ului, masurate in perioada ianuarie -decembrie 1993 pe raul Aries. Datele au fost obtinute de la R.A. Apele Romane.
|
PH |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Debit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
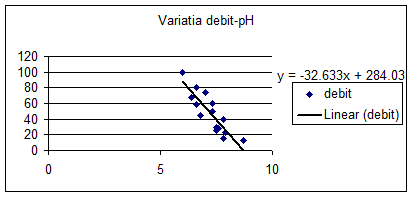
Figura 45 Dreapta de regresie
Se observa ca pH-ul scade odata cu cresterea debitului. La debite mai mari procesele hidrice (dizolvare, dilutie etc) fiind mai accentuate. La valori mai mici ale debitului, pH-ul creste devenind usor acid (7,6 – 7,9) sau acid (8,7). Coeficientul de corelatie este r=-0,87946; avem astfel o corelatie inversa stransa.
In al doilea exemplu am determinat curba de regresie corespunzatoare variatiei debitului si suspensiilor. Datele au fost obtinute in urma analizelor fizico-chimice efectuate pe Valea Zalaului, de pe teritoriul municipiului Zalau in anul 1995.
|
debit |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
susp. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
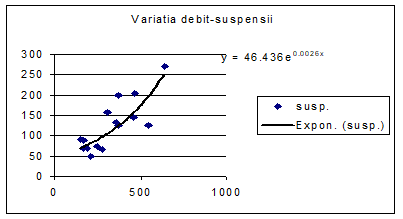
Figura 46 Curba exponentiala de regresie
In figura 46 se distinge faptul ca odata cu cresterea debitului cantitatea de suspensii din apa creste exponential. Datorita curentului, particulele de dimensiuni mari de pe fundul albiei sunt antrenate in miscare, devenind suspensii. In cazul unor debite mai mici, cand scurgerea este mai lina, doar particulele de dimesiuni mici sunt antrenate in miscare. Facem observatia ca acesta lege nu este atat de reprezentativa ca si cea din exemplul precedent.
Calculele au fost facute cu programul de calcul tabelar Excel.
Regresia multipla.
Consideram cazul in care variabila Z depinde de doua variabile X si Y. Se doreste obtinerea dependentei
Z = a X + b Y + c
astfel incat suma
![]()
sa fie minima. Se obtine
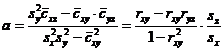
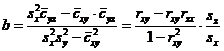
si ecuatia de regresie:
![]()
Reprezentata geometric aceasta ecuatie este un plan in spatiul oxyz. Interpretarea este urmatoatrea: acest plan este planul care ajusteaza cel mai bine sirurile xi si yi, i=1,, n. Cu alte cuvinte, daca Z reprezinta efectul, X si Y reprezinta cauzele, in consecinta, Z arata dependenta liniara de cele doua variabile X si Y luate impreuna.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








