
| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Informatica
|
|
Qdidactic » stiinta & tehnica » informatica Determinarea arborelui de acoperire minim al unui graf ponderat. Algoritmul lui Prim |
Determinarea arborelui de acoperire minim al unui graf ponderat. Algoritmul lui Prim
Determinarea arborelui de acoperire minim al unui graf ponderat. Algoritmul lui Prim
1. Scopul lucrarii este prezentarea modului de determinare a arborelui de acoperire minim pentru grafuri ponderate impreuna cu un exemplu pentru implementarea grafurilor cu matrici de adiacenta.
2. Aspecte teoretice.
2.1. Grafuri ponderate si arborele de acoperire minim
Grafurile ponderate sunt cele in care tuturor arcelor li se asociaza ponderi (greutate, cost, valoare etc.). In ceea ce priveste reprezentarea unor astfel de grafuri, structurile de date utilizate sunt similare ca si in cazul grafurilor neorientate si neponderate, cu urmatoarele deosebiri:
- in cazul reprezentarii prin matrice de adiacenta, matricea va contine ponderi in locul valorilor booleene
 -
in cazul reprezentarii prin structuri de adiacenta,
fiecarui element din cadrul listelor de adiacente i se poate
adauga un camp suplimentar pentru memorarea ponderii.
-
in cazul reprezentarii prin structuri de adiacenta,
fiecarui element din cadrul listelor de adiacente i se poate
adauga un camp suplimentar pentru memorarea ponderii.
O problema fundamentala in cazul grafurilor ponderate o reprezinta determinarea arborelui de acoperire minim. Un arbore de acoperire a unui graf ponderat este un arbore liber (graf conex aciclic) care cuprinde toate nodurile din multimea de noduri ale grafului, dar numai anumite arce care conecteaza aceste noduri. Costul unui arbore de acoperire este suma costurilor tuturor arcelor cuprinse in arbore.
Un arbore de acoperire minim al unui graf ponderat este arborele de acoperire al carui cost este cel putin la fel de mic ca si costul oricarui arbore de acoperire al grafului. Pentru un graf pot exista mai multi arbori de acoperire minimi.
Exista mai multi algoritmi utilizati in acest sens, dintre care se remarca algoritmul lui Prim si tehnica cautarii bazate pe prioritate. Indiferent de metoda utilizata, determinarea arborelui de acoperire minim se bazeaza in esenta pe urmatoarea proprietate a arborilor de acoperire minimi: fie G = (N, A) un graf conex si o functie de cost definita pe multimea arcelor sale, A. Fie U o submultime proprie a multimii N de noduri. Daca (u, v) este un arc cu costul cel mai scazut astfel incat u U si v N - U, atunci exista un arbore de acoperire minim care include pe (u, v) ca si arc.
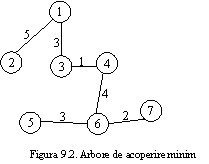
In figura 9.2 este reprezentat un arbore de acoperire minim pentru graful de mai sus.
2.2. Algoritmul lui Prim
Principiul algoritmului este urmatorul: fie G graful ponderat pentru care se doreste determinarea arborelui de acoperire minim si fie N multimea nodurilor acestuia. Algoritmul incepe prin selectia unui nod de pornire si introducerea lui in multimea U. In continuare, intr-o maniera ciclica, se selecteaza la fiecare pas arcul cu cost minim (u, v) care conecteaza un nod din multimea U cu un alt nod din multimea V = N - U si se adauga acest arc arborelui de acoperire minim, iar nodul v lui U. Ciclul se repeta pana cand toate nodurile au trecut in submultimea U, adica U = N.
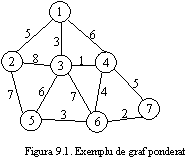
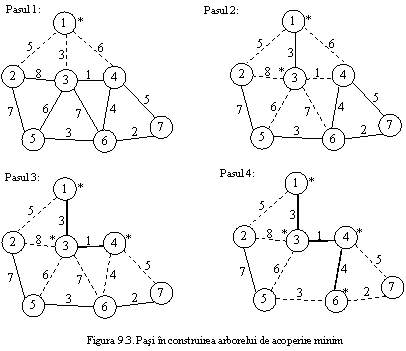
Mai jos sunt prezentati primii pasi pentru determinarea arborelui de acoperire minim pentru graful din figura 9.1, pornind de la nodul 1 (initial U = ) (cu * sunt marcate nodurile alese, linia ingrosata reprezinta arcele alese, cea intrerupta - arcele candidate la urmatoarea alegere, adica cele ce leaga noduri alese cu noduri nealese inca si dintre care va fi ales cel cu costul minim, linia obisnuita - arcele care conecteaza noduri nealese, iar arcele nealese care conecteaza nodurile deja alese nu mai sunt reprezentate pentru ca nu mai pot face parte din arbore).
|
Implementarea propriu-zisa a algoritmului lui Prim prezentata in continuare se refera la cazul implementarii grafurilor prin matrici de adiacenta. O modalitate simpla de a afla arcul cu costul cel mai redus dintre submultimile de noduri U si V = N - U, este aceea de a pastra la fiecare pas doua tablouri:
- tabloul apropiat - pastreaza pe pozitia i nodul din U care este la momentul curent cel mai apropiat de nodul i din N - U;
- tabloul costMin - pastreaza pe pozitia i costul arcului (i, apropiat[i]).
Aceasta pentru ca pentru introducerea unui nod din N - U in U nu avem nevoie decat de un arc. Asa cum se vede in figura 9.3, la pasul 3, avem in multimea de arce candidate si (1, 2) cu costul 5, si (3, 2) cu costul 8. Pentru a introduce nodul 2 vom alege un arc cu costul cel mult 5, deci oricum nu vom alege arcul (3, 2) si putem sa-l eliminam dintre arcele candidate. Astfel, la fiecare pas, vom avea arcul cu cost minim care leaga fiecare nod neales cu unul ales si din aceasta multime va fi ales arcul cu cost minim.
La fiecare pas se parcurge tabloul costMin pentru a gasi nodul k din N - U cel mai apropiat de un nod din U. Se tipareste arcul (apropiat[k], k) ca apartinand arborelui de acoperire minim, dupa care se actualizeaza tablourile costMin si apropiat, luand in considerare ca nodul k a fost adaugat lui U.
Se va face conventia ca daca arcul (i, j) nu exista, arc[i, j] are o valoare mare, specifica, mai mare decat orice cost posibil, dar mai mica decat valoarea infinit utilizata in cadrul algoritmului. De asemenea, ori de cate ori se gaseste un nod k pentru a fi introdus in arborele de acoperire (multimea U), se face costMin[k] egal cu infinit (o valoare foarte mare, mai mare decat cea de la initializarea arcelor inexistente), astfel incat acel nod sa nu mai poata fi selectat in continuare si inclus in U. Deci, valoarea infinit este mai mare decat costul oricarui arc al grafului sau decat costul asociat lipsei arcului.
In figura 9.4 sunt prezentati primii pasi in constructia arborelui de acoperire minim folosind cele doua tablouri, pornind tot de la nodul 1. Sunt date valorile elementelor tablourilor apropiat si, respectiv, costMin la fiecare pas. Pentru o urmarire mai usoara, pentru tabloul apropiat am tiparit pe fiecare pozitie cheia nodului cel mai apropiat si nu indicele lui in matrice (cu I am simbolizat valoarea infinit, iar cu M - valoarea mare).
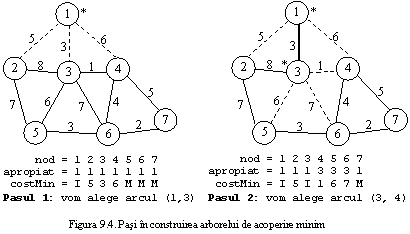
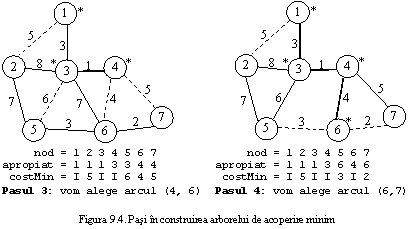
Pasul 5: nod = 1 2 3 4 5 6 7
apropiat = 1 1 1 3 6 4 6
costMin = I 5 I I 3 I I -> vom alege arcul (6 5)
Pasul 6: nod = 1 2 3 4 5 6 7
apropiat = 1 1 1 3 6 4 6
costMin = I 5 I I I I I -> vom alege arcul (1 2)
Astfel, pentru graful din figura 9.1, aplicarea algoritmului lui Prim conduce la arborele de acoperire minim format din arcele: (1, 3), (3, 4), (4, 6), (6, 7), (6, 5) si (1,2), reprezentat in figura 9.2.
3. Problema rezolvata
Se dau n orase, impreuna cu costul cablului necesar conectarii directe a anumitor perechi de orase. Sa se aleaga acele conectari directe care asigura existenta unei legaturi intre oricare doua orase dintre cele n date (intre care poate exista legatura), astfel incat costul total al cablului pentru conectare sa fie minim si sa se calculeze acest cost.
Rezolvare
Problema se rezolva determinand arborele de acoperire minim pentru graful conectarilor intre orase. Vom aplica algoritmul lui Prim, implementat cu observatiile de mai sus in functia Prim. Datele problemei vor fi citite dintr-un fisier cu formatul: numarul de conectari directe, apoi, pentru fiecare conectare directa: identificatorii celor doua orase conectate si costul conectarii (identificatorii si costul se considera a fi un numere intregi). Pentru graful din figura 9.1 fisierul arata astfel:
12 1 2 5 1 3 3 1 4 6 2 3 8 2 5 7 3 4 1 3 5 6 3 6 7 4 6 4 4 7 5
5 6 3 6 7 2
Programul functioneaza si daca graful nu este conex. Daca graful contine noduri izolate, in fisier vom avea, de exemplu, pentru un nod izolat cu cheia 8: 8 8 0
#include <stdio.h>
#include <conio.h>
#include <stdlib.h>
#define nrMaxN 20
#define mare 2000
#define inf 20000
typedef struct _nodGnodG;
nodG nod[nrMaxN];
int arc[nrMaxN][nrMaxN], nrN, nrA,
costMin[nrMaxN], apropiat[nrMaxN];
int m[3], i, j, k, min, idxMin, costTotal;
FILE *f;
int CautaNod(int k)
void AfisImplGraf(void)
printf('- %dn ', nod[i].cheie);
}
void Prim()
for(j=0;j<nrN-1;j++)
if(min!=mare)
costMin[idxMin] = inf;//marcam nodul ca inclus
for(k=1;k<nrN;k++)//actualizam apropiat si costMin
if(arc[idxMin][k]<costMin[k]&&
costMin[k]<inf)
}
int main(void)
fscanf(f, '%d', &nrA);
nrN = 0;//nr. de noduri
for(i=0;i<nrA;i++)
}
arc[p[0]][p[1]] = arc[p[1]][p[0]] = m[2];
//adaug muchia
}
fclose(f);
AfisImplGraf();
printf('nConectarile alese sunt:n');
Prim();
printf('nCostul conectarii in acest mod este %d.', costTotal);
getch();
return 0;
4. Probleme propuse
4.1. Un graf este complet daca fiecare nod este conectat in mod direct cu toate celelalte noduri. Dandu-se un graf neorientat, ponderat si complet cu N>5 noduri, generat aleator, sa se determine:
arborele de acoperire minim pentru graful dat, utilizand algoritmul lui Prim
care sunt arcele prin suprimarea carora arborele de acoperire minim rezultat pentru noul graf se modifica fata de cel determinat initial?
Sa se realizeze o statistica despre cum variaza costul total al arborilor de acoperire minimi in functie de costul arcului care se suprima.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
||||||||||||||||||||||||
Proiecte pe aceeasi tema | ||||||||||||||||||||||||
|
| ||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||








