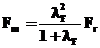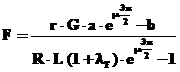Aeronautica Comunicatii Drept Informatica Nutritie Sociologie Tehnica mecanica Tehnica mecanica Qdidactic » stiinta & tehnica » tehnica mecanica Aplicatii tehnice ale staticii Aplicatii tehnice ale staticii APLICATII  TEHNICE ALE STATICII 1. Generalitati Obiectul acestui capitol este studiul echilibrului unor sisteme de corpuri intilnite in tehnica sub denumirea de dispozitive mecanice simple .Aceste dispozitive simple sunt folosite pentru deplasarea punctului de aplicatie ale unor forte mari numite forte rezistente ( caz particular greutati ) cu ajutorul unor forte sau cupluri de valori mai mici denumite forte sau cupluri motoare , accesibile unor actionari manuale . 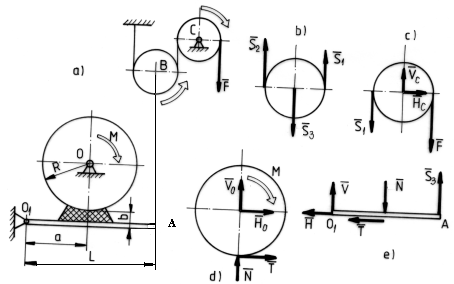Functionarea acestor dispozitive simple poate fi explicata pe baza unor notiuni utilizate in Teoria Sistemelor si indicate in fig. 1. Fig.1. Unde : Fr , Mr - forta , respectiv cuplul rezistent Fm , Mm - forta , respectiv cuplul motor Deoarece toate ecuatiile de echilibru ale corpurilor considerate rigide , ce alcatuiesc sistemul aflat in studiu , sunt liniare si omogene in raport cu elementele mecanice motoare si rezistente , dupa ce se elimina din aceste ecuatii reactiunile rezulta intotdeauna o relatie de forma : Fm = lF Fr unde : lF este raportul de transmitere a fortei , si este o marime adimensionala . Raportul de transmitere a fortei este cuprins intre doua limite care corespund : una tendintei de miscare la limita in sensul fortei rezistente si cealalta tendintei de miscare in sensul fortei motoare . Deci putem scrie                                                                      (2) In absenta frecarilor :                                                                                                                                           (3) Din analiza relatiei (2) rezulta doua modalitati de impiedicare a celor doua tendinte de miscare denumite : autofranare si autoblocare . Fenomenul de autofranare O masina sau un mecanism cu un singur grad de mobilitate are doua posibilitati de miscare : una in sensul provocat de forta de rezistenta , si cealalta in sensul determinat de forta motoare.Este cunoscut faptul ca in tehnica se cauta a se evita prima posibilitate intrucat s-ar putea provoca accidente , masinile respective fiind prevazute cu dispozitive care blocheaza acest sens al miscarii (frane , clicheti) . Este insa de dorit ca o asemenea miscare sa fie impiedicata si prin actiunea sistemului de forte care apar intre corpurile rigide ce alcatuiesc masina , in acest caz apare fenomenul de autofranare. Conditia de autofranare este:                                                                                     (4) unde semnul egal indica un echilibru la limita de alunecare . 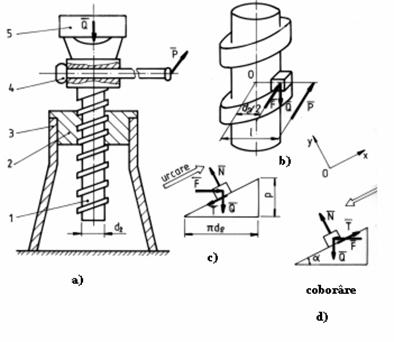Fenomenul de autoblocare In functionarea dispozitivelor simple pot exista anumite pozitii pentru care incercarea de a-l pune in miscare in sensul determinat de forta motoare sa conduca la valori infinit de mari ale acesteia ; in acest caz apare fenomenul de autoblocare . Fenomenul de autoblocare si de autofranare va fi analizat in mod concret la mecanismul surub-piulita. 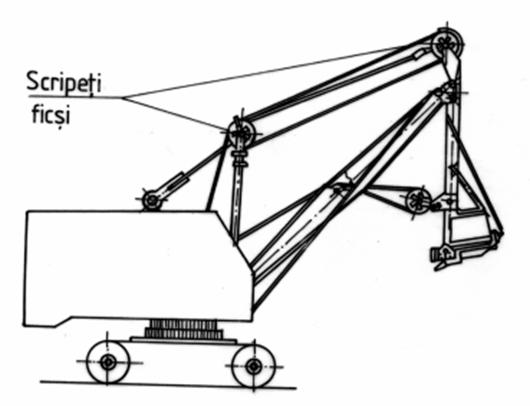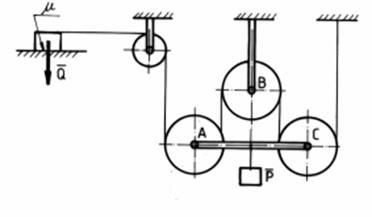Dispozitivele mecanice simple pot fi impartite in doua tipuri : a.     tipul parghiilor : parghia , aparate de cantarit , sisteme de parghii articulate , scripeti si sisteme de scripeti . b.     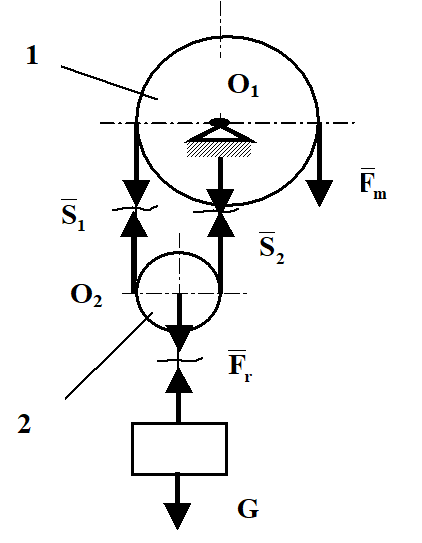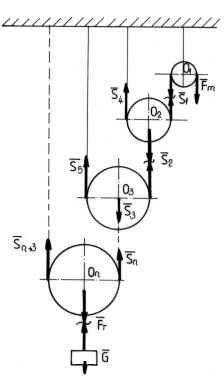tipul planului inclinat : planul inclinat , pana , surubul , mecanismul surub-piulita 2. Sisteme de scripeti 2.1. Scripetele simplu Scripetele este alcatuit dintr-un disc de raza R, pe a carui periferie s-au executat unul sau mai multe santuri de ghidare pe unde poate sa treaca un cablu sau un lant , care materializeaza firul teoretic . Scripetele se numeste fix sau mobil dupa cum axul sau este fixat sau se poate deplasa . 2.2. 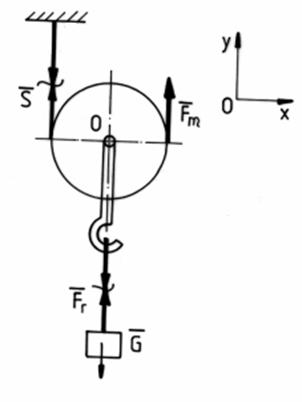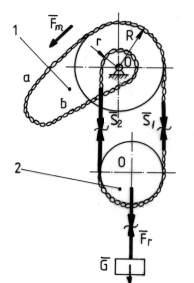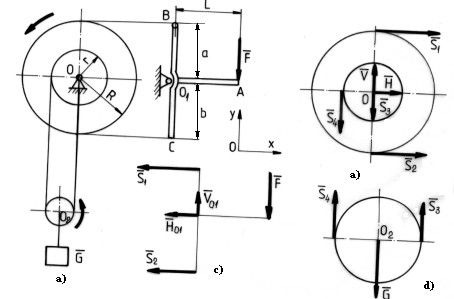Scripetele fix Se considera un scripete fixat cu articulatia O , al carui fus are raza r si coeficientul de frecare . De un capat al firului se pune corpul care trebuie ridicat , greutatea corpului constituind forta de rezistenta , iar de celalalt capat se trage in jos cu o forta care reprezinta forta motoare . 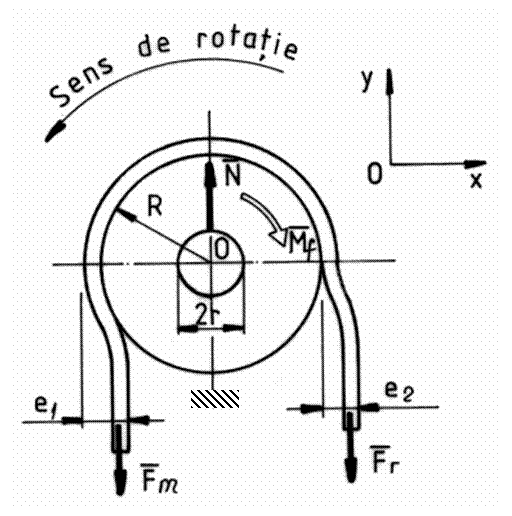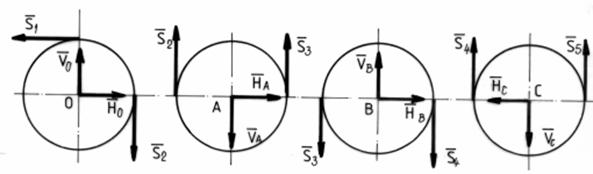Deoarece cablurile nu sunt perfect flexibile ci opun rezistenta la schimbarea formei , atunci cand scripetele se roteste , ramura care se infasoara se opune trecerii de la forma rectilinie la cea circulara , iar ramura care se desfasoara se opune trecerii de la forma circulara la forma rectilinie si ,ca urmare, apar abaterile e1 si e2 ( fig.2 ) Fig.2 Pentru schema de calcul din fig.2 ecuatiile scalare de echilibru sunt : SFiy = 0 ; N = Fm + Fr (5) SMio = 0  ; Fm ( R - e1 ) - Fr ( R + e2 ) = 0 (6) la limita :         Mf = m r N (7) Rezolvand ecuatiile (5) , (6) si (7) obtinem :

Deoarece l_F > , forta motoare F_m este mai mare decat cea rezistenta F_r , fapt care reduce avantajul scripetelui cu ax fix numai la schimbarea sensului de actionare .

In fig.3 sunt aratate modalitati de folosire a scripetilor ficsi in cadrul elementelor componente ale unui excavator .

Fig.3

2.3.Scripetele mobil

Pentru scripetele mobil eliberat de legaturi din fig.4 , ecuatia scalara de echilibru este :

S F_iy = 0     ; S = F_r - F_m (9)

Relatia (8) poate fi scrisa pentru S si F_m sub forma :

F_m = l_F S (10)

Introducand (10) in (9) obtinem :

(11)

Fig.4

Din analiza relatiei (11) rezulta F_m < F_r

Pentru a beneficia de avantajul reducerii fortei motoare oferit de catre scripetele mobil cat si de cel al schimbarii sensului de actionare , in tehnica se folosesc combinatii de scripeti mobili si ficsi sub denumirea de sisteme de scripeti .

Din cadrul sistemelor de scripeti se vor studia : scripetele dublu , scripetele diferential si palanul exponential .

2.4. Scripetele dublu

Un sistem format dintr-un scripete fix (1) si unul mobil (2) se numeste scripete

dublu si este prezentat in figura 5.

Fig.5

Pentru fig.5 , folosind relatiile (9) si (11) obtinem :

Pentru scripetele fix (1)

F_m = l_F S₁ (12)

2.5. Scripetele diferential

Scripetele diferential ( prezentat in figura 6) este compus dintr-un troliu (1) si scripetele mobil (2) , peste care este trecut un lant continuu de care se trage cu forta atat pe ramura a cat si pe ramura b .

Fig.6

Izoland corpurile putem scrie:

S F_iy = 0 ; S₁ + S₂ = F_r (17)

Aplicatia

Sa se determine relatia dintre F_m si F_r la un sistem de scripeti format dintr-un scripete fix (1) si n scripeti mobili (2) din fig.7.

Fig.7

Rezolvare

Aplicand relatiile (8) si (11) obtinem :

de unde :

Neglijand frecarile rezulta : l care introdus in (22) se obtine :

3. Mecanismul surub-piulita

In fig.8 a , este reprezentat un cric mecanic , utilizat pentru ridicarea si coborarea greutatii . Cricul este alcatuit din :

- surub avand filetul cu profil patrat ;

- piulita fixa avand filetul cu acelasi profil ;

- suport de sustinere ;

- brat de actionare ;

- greutatea  care trebuie ridicata .

Cunoscand : coeficientul de frecare m dintre surub si piulita , lungimea l a bratului (4) , diametrul mediu al filetului d₂ , si unghiul de inclinare a al filetului , se pune problema determinarii fortei aplicata bratului (4) pentru ridicarea greutatii .

Fig.8

In baza analogiei functionale existente intre mecanismul surub-piulita si planul inclinat rezulta ca strangerea sau desfacerea piulitei unei asamblari filetate aflate sub actiunea unei forte axiale este echivalenta cu ridicarea respectiv coborarea unui corp de greutate pe un plan inclinat , avand unghiul de inclinare al filetului a ( fig. 8 c,d ) .

In aceasta acceptiune , pentru fig.8 c , pot fi scrise ecuatiile scalare de echilibru :

SF_ix = 0 ; Fcosa T Qsina (25)

SF_iy = 0 ; N = Qcosa + Fsina (26)

T m N (27)

tinand cont ca :

m = tg j

prin rezolvarea relatiilor (25 + 27) se obtine :

F Q tg (a j (29)

Analizand fig. 27 , b , rezulta :

Observatii

1. Daca (a j p T tg (a j rezulta P deci mecanismul

surub - piulita este autoblocat .

2. Pentru echilibrul surubului la limita de miscare in sensul desfacerii (fig. 8 , d)

se obtine :

Daca P = 0 , rezulta a j (33)

Relatia (33) reprezinta conditia ca surubul sa se autofraneze , adica sa nu se desurubeze din piulita sub actiunea fortei  chiar daca = 0 .

Aplicatia 2

Se considera cricul mecanic din fig. 8 , a , pentru care se cunosc :

d₂ = 52 mm , p = 12,7 mm , l = 8,00 mm ,coeficientul de frecare dintre surub si piulita

m = 0,1 , coeficientul de frecare dintre greutatea Q = 400 N si suprafata frontala de sustinere

(de forma inelara de raza medie d₁ = 50 mm ) m

Sa se determine :

unghiul mediu a al inclinarii filetului ;

daca surubul se autofraneaza ;

momentul necesar strangerii surubului ;

momentul de frecare pe suprafata frontala de sustinere ;

momentul total necesitat de ridicarea greutatii  ;

forta P necesara actionarii bratului (4) pentru ridicarea greutatii Q ;

forta P folosita pentru coborarea greutatii Q .

Rezolvare

deci surubul se autofraneaza .

5) M_t = M + M_f = 1,965 + 1,2 = 3,065 N m

M_t1 = M₁ + M_f = 0,2298 + 1,2 = 1,4298 N m

Aplicatia  3

Fig.9,a

Fig.9,b Fig.9,c Fig.9,d Fig.9,e

Fig.9,f Fig.9,g

Rezolvare

Izoland corpurile se obtin schemele de calcul din fig. 9 ,b , c , d, e , f , g , pentru care ecuatiile scalare de echilibru sunt :

T = mN ;          N = Q ; S₁ = T (1)

S₂ = l_FS₁ ;       S₃ = l_FS₂ ; S₄ = l_FS₃ ;     S₅ = l_FS₄ (2)

S₂ + S₃ = V_A ; S₄ + S₅ = V_B ; V_A + V_B = P (3)

Rezolvand sistemul de ecuatii (1),(2) si (3) se obtine :

P = l_F l_F l _F m Q

Aplicatia 4

Pe tamburul exterior al unui troliu este infasurata o banda legata de punctele B si C ale unei parghii. De axul scripetelui mobil O₂ avand raportul de transmisie l_F , este suspendata greutatea . Cunoscand coeficientul de frecare m dintre banda si troliu , sa se determine valoarea minima a fortei F necesare pentru franarea troliului .

Fig.10

Rezolvare

aM_iO1 = 0 ; F L - S₂b + S₁a = 0

aM_iO = 0 ; S₂R + S₄r S₁R = 0 (I)

aF_iy = 0     ; S₃ + S₄ - G = 0

la care se adauga relatiile :

(II)

Rezolvand (I) si (II) se obtine :

Aplicatia 5

Arborele unei transmisii mecanice este actionat de momentul M de la un electromotor . Cunoscand coeficientul de frecare m dintre sabot si arbore precum si raportul de transmisie l_F al fiecarui scripete , sa se determine valoarea minima a fortei F necesara pentru ca arborele sa fie franat .

Rezolvare

Izoland corpurile se obtin schemele de calcul din fig.11 , b , c , d , e , pentru care pot fi scrise ecuatiile scalare de echilibru :

aF_iy = 0     ; S₁ + S₂ = S₃

aM_iO1 = 0 ; S₃L + Tb Na = 0 (I)

aM_iO = 0 ; TR - M = 0

la care se adauga relatiile :

F = l_F S₁ ; S₁ = l_F S₂ ; T = m N (II)

Rezolvand sistemul format din (I) si (II) se obtine :

Contact |- ia legatura cu noi -|
Adauga document |- pune-ti documente online -|
Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -|
Copyright © |- 2024 - Toate drepturile rezervate -|

Tehnica mecanica

Auto

Documente online pe aceeasi tema Crearea filmului ce urmeaza a fi foto-expus pe sita serigrafica Instructiuni de sudare Calculul unui acumulator de presiune - recipient de hidrofor Simetria la translatiile temporale - simetriile si legile de conservare - mecanica Instructiuni de sudare - specificatia procedurii de sudare (WPS) Chiestionar mecanica Sistemul de by-pass inalta presiune Puterea electromotorului - alegerea motorului - randamentul total al transmisiei Aplicatii tehnice ale staticii Tehnologia prelucrarii electrochimice - principalele operatii

Ramai informat Informatia de care ai nevoie Acces nelimitat la mii de documente. Online e mai simplu. Contribuie si tu! Adauga online documentul tau.