| Aeronautica | Comunicatii | Drept | Informatica | Nutritie | Sociologie |
| Tehnica mecanica |
Tehnica mecanica
|
|
Qdidactic » stiinta & tehnica » tehnica mecanica MACHINERY FUNDAMENTALS - A Simple Rotating Loop between Curved Pole Faces |
MACHINERY FUNDAMENTALS - A Simple Rotating Loop between Curved Pole Faces
DC MACHINERY FUNDAMENTALS
Summary:
A Simple Rotating
The Voltage Induced in a Rotating
Getting DC voltage out of the Rotating Loop
The Induced Torque in the Rotating
Commutation in a Simple Four-Loop DC Machine
Problems with Commutation in Real Machine
Armature Reaction
L di/dt Voltages
Solutions to the Problems with Commutation
The Internal Generated Voltage and Induced Torque Equations of Real DC Machine
The Construction of DC Machine
Power Flow and Losses in DC Machines
A Simple Rotating
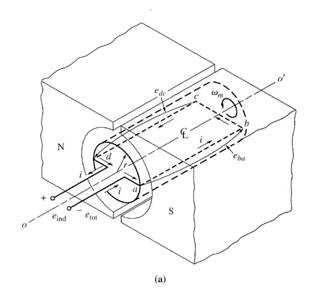 The simplest rotating dc machine is shown below:
The simplest rotating dc machine is shown below:
It consists of
a single loop of wire rotating about a fixed axis. The rotating part is called rotor, and
the stationary part is the stator. The magnetic
field for the machine is supplied by the magnetic north and south
poles. Since the air gap is of
uniform width, the reluctance is the same everywhere under the pole faces.
The Voltage Induced in a Rotating
 If the rotor is rotated, a voltage will be induced in the wire
loop. To determine the magnitude and
shape of the voltage, examine the figure below:
If the rotor is rotated, a voltage will be induced in the wire
loop. To determine the magnitude and
shape of the voltage, examine the figure below:
To determine the total voltage etot on the loop, examine each segment of the loop separately and sum all the resulting voltages. The voltage on each segment is given by eind = (v x B) l
Thus, the total induced voltage on the loop is: eind = 2vBl
When the loop rotates through 180°, segment ab is under the north pole face instead of the south pole face. At that time, the direction of the voltage on the segment reverses, but its magnitude remains constant. The resulting voltage etot is shown below:
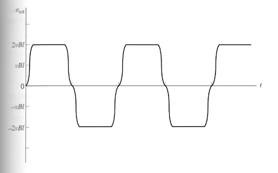
There is an alternative way to express the eind equation, which clearly relates the behaviour of the single loop to the behaviour of larger, real dc machines. Examine the figure below:
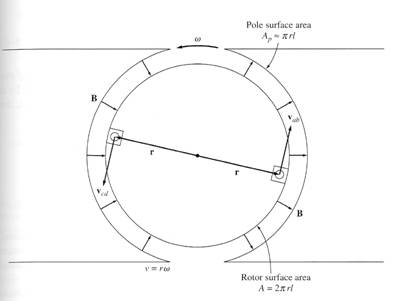
The tangential velocity v of the edges of the loop can be expressed as v = rω. Substituting this expressing into the eind equation before gives:
eind = 2rωBl
The rotor surface is a cylinder, so the area of the rotor surface A is equal to 2πrl. Since there are 2 poles, the area under each pole is Ap = πrl. Thus,
![]()
Since the flux density B is constant everywhere in the air gap under the pole faces, the total flux under each pole is = APB. Thus, the final form of the voltage equation is:
![]()
In general, the voltage in any real machine will depend on the same 3 factors:
- the flux in the machine
- The speed of rotation
- A constant representing the construction of the machine.
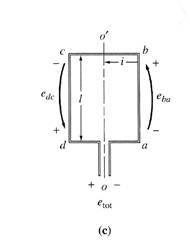
Getting DC voltage out of the Rotating
The voltage out of the loop is alternately a constant positive and a constant negative value. How can this machine be made to produce a dc voltage instead of the ac voltage?
This can be done by using a mechanism called commutator and brushes, as shown below:
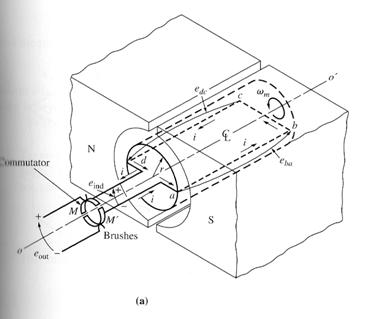
Here 2 semicircular conducting segments are added to the end of the loop, and 2 fixed contacts are set up at an angle such that at the instant when the voltage in the loop is zero, the contacts short-circuit the two segments.
Thus, every time the voltage of the loop switches direction, the contacts also switches connections, and the output of the contacts is always built up in the same way. This connection-switching process is known as commutation. The rotating semicircular segments are called commutator segments, and the fixed contacts are called brushes.
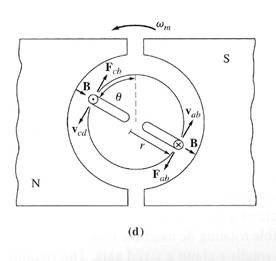
The Induced Torque in the Rotating
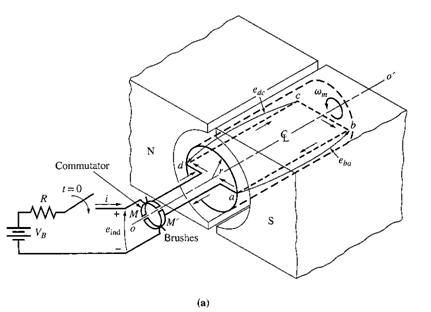 Suppose a battery is now connected to the machine as shown here,
together with the resulting configuration:
Suppose a battery is now connected to the machine as shown here,
together with the resulting configuration:
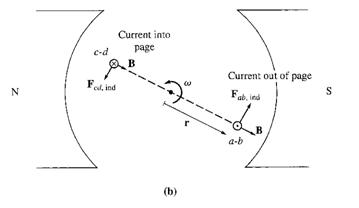
How much torque will be produced in the loop when the switch is closed? The approach to take is to examine one segment of the loop at a time and then sum the effects of all the individual segments. The force on a segment of the loop is given by : F = i (l x B) , and the torque on the segment is t = r F sin θ.
The resulting total induced torque in the loop is:
t
By using the fact that AP = πrl and = APB, the torque expression can be reduced to:
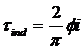
In general, the torque in any real machine will depend on the same 3 factors:
- The flux in the machine
- The current in the machine
- A constant representing the construction of the machine.
2. Commutation in a Simple Four-Loop DC Machine
Commutation is the process of converting the ac voltages and currents in the rotor of a dc machine to dc voltages and currents at its terminals. A simple 4 loop, 2 pole dc machine is shown here:
at ωt=0°
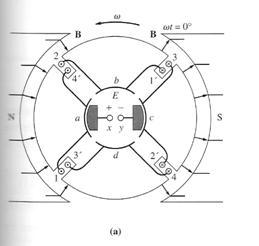
This machine has 4 complete loops buried in slots carved in the laminated steel of its rotor. The pole faces of the machine are curved to provide a uniform air-gap width and to give a uniform flux density everywhere under the faces.
The 4 loops of this machine are laid into the slots in a special manner. The "unprimed" end of each loop is the outermost wire in each slot, while the "primed" end of each loop is the innermost wire in the slot directly opposite. The winding's connections to the machine's commutator are shown below:
|
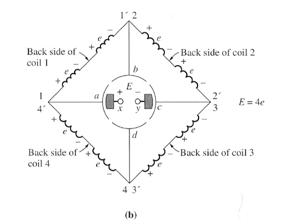
Notice that loop 1 stretches between commutator segments a and b, loop 2 stretches between segments b and c, and so forth around the rotor.
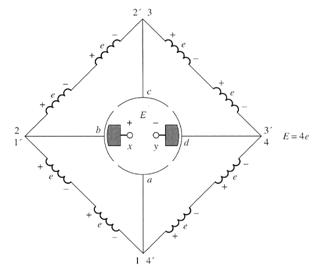
At the instant shown in figure (a), the 1, 2, 3' and 4' ends of the loops are under the north pole face, while the 1', 2', 3 and 4 ends of the loops are under the south pole face.
The voltage in each of the 1, 2, 3' and 4' ends of the loops is given by:
eind = (v x B) l
eind = vBl (positive out of page)
The voltage in each of the 1', 2', 3 and 4 ends of the loops is given by:
eind = (v x B) l
eind = vBl (positive into the page)
The overall result is shown in figure (b). Each coil represents one side (or conductor) of a loop. If the induced voltage on any one side of a loop is called e=vBl, then the total voltage at the brushes of the machine is E = 4e (ωt=0°)
Notice that there are two parallel paths for current through the machine. The existence of two or more parallel paths for rotor current is a common feature of all commutation schemes.
 What happens to the voltage E of the terminals as the rotor
continues to rotate? Examine the figures
below:
What happens to the voltage E of the terminals as the rotor
continues to rotate? Examine the figures
below:
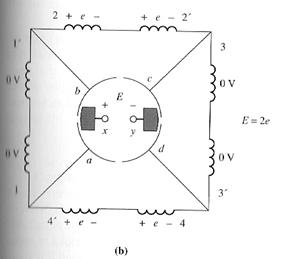
at ωt=45°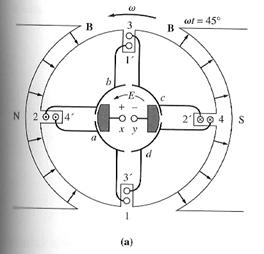
This figure shows the machine at time ωt=45°. At that time, loops 1 and 3 have rotated into the gap between the poles, so the voltage across each of them is zero. Notice that at this instant the brushes of the machine are shorting out commutator segments ab and cd. This happens just at the time when the loops between these segments have 0V across them, so shorting out the segments creates no problem. At this time, only loops 2 and 4 are under the pole faces, so the terminal voltage E is given by:
E = 2e (ωt=45°)
Now, let the rotor continue to turn another 45°. The resulting situation is shown below:
at ωt=90°
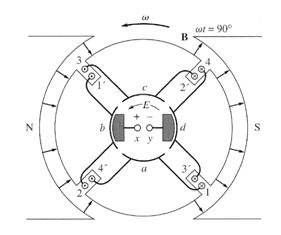
Here, the 1', 2, 3, and 4' ends of the loops are under the north pole face, and the 1, 2', 3' and 4 ends of the loops are under the south pole face. The voltages are still built up out of the page for the ends under the north pole face and into the page for the ends under the south pole face. The resulting voltage diagram is shown here:
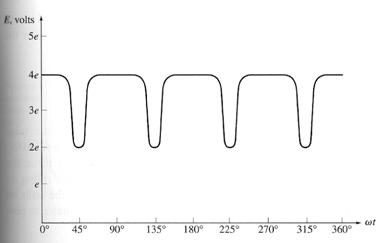
There are now 4 voltage-carrying ends in each parallel path through the machine, so the terminal voltage E is given by:
E = 4e (ωt=90°)
Notice that the voltages on loops 1 and 3 have reversed between the 2 pictures (from ωt=0° to ωt=90°), but since their connections have also reversed, the total voltage is still being built up in the same direction as before. This is the heart of every commutation scheme.
3. Problems with Commutation in Real Machine
In practice, there are two major effects that disturb the commutation process:
- Armature Reaction
- L di/dt voltages
Armature Reaction
If the magnetic field windings of a dc machine are connected to a power supply and the rotor of the machine is turned by an external source of mechanical power, then a voltage will be induced in the conductors of the rotor. This voltage will be rectified into dc output by the action of the machine's commutator.
Now, connect a load to the terminals of the machine, and a current will flow in its armature windings. This current flow will produce a magnetic field of its own, which will distort the original magnetic field from the machine's poles. This distortion of the flux in a machine as the load is increased is called armature reaction. It causes 2 serious problems in real dc machine.
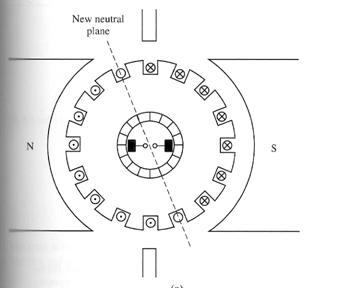
Problem 1 : Neutral-Plane Shift
The magnetic neutral plane is defined as the plane within the machine where the velocity of the rotor wires is exactly parallel to the magnetic flux lines, so that eind in the conductors in the plane is exactly zero.
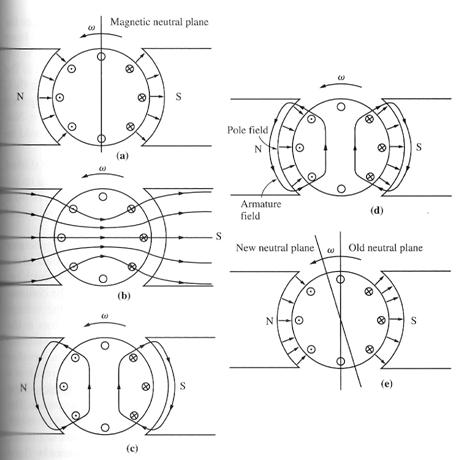
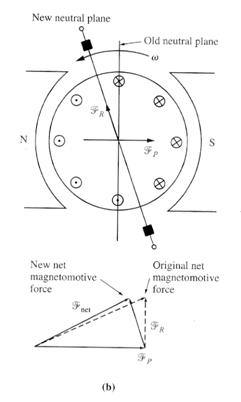
Figure (a) shows a two poles machine. Notice that the flux is distributed uniformly under the pole faces. The rotor windings shown have voltages built up out of the page for wires under the north pole and into the page for wires under the south pole face. The neutral plane in this machine is exactly vertical.
Now, suppose a load is connected to this machine so that it acts as a generator. Current will flow out of the positive terminal of the generator, so current will be flowing out of the page for wires under the north pole face and into the page for wires under the south pole face. This current flow produces a magnetic field from the rotor windings, figure (c).
This rotor magnetic field affects the original magnetic field from the poles that produced the generator's voltage in the first place. In some places under the pole surfaces, it subtracts from the pole flux, and in other places it adds to the pole flux. The overall result is that the magnetic flux in the air gap of the machine is skewed, figure (d) and (e). Notice that the place on the rotor where the induced voltage in a conductor would be zero (the neutral plane) has shifted.
For the generator shown here, the magnetic neutral plane shifted in the direction of rotation. If this machine had been a motor, the current in its rotor would be reversed and the flux would bunch up in the opposite corners from the bunches shown in the figure. As a result, the magnetic neutral plane would shift the other way.
In general, the neutral-plane shifts in the direction of motion for generator and opposite to the direction of motion for a motor. Furthermore, the amount of the shift depends on the amount of rotor current and hence on the load of the machine.
What is so important regarding the neutral-plane shift?
The commutator must short out commutator segments just at the moment when the voltage across them is equal to zero. If the brushes are set to short out conductors in the vertical plane, then the voltage between segments is indeed zero until the machine is loaded. When the machine is loaded, the neutral-plane shifts, and the brushes short out commutator segments with a finite voltage across them. The result is a current flow circulating between the shorted segments and large sparks at the brushes when the current path is interrupted as the brush leaves a segment. The end result is arcing and sparking at the brushes. This is a very serious problem, since it leads to drastically reduced brush life, pitting of the commutator segments, and higher maintenance costs. Notice that this problem cannot be fixed even by placing the brushes over the full-load neutral plane, because then they would spark at no load.
In extreme cases, the neutral-plane shift can even lead to flashover in the commutator segments near the brushes. The air near the brushes in a machine is normally ionized as a result of the sparking on the brushes. Flashover occurs when the voltage of adjacent commutator segments gets large enough to sustain an arc in the ionized air above them. If flashover occurs, the resulting arc can even melt the commutator's surface.
Problem 2 : Flux Weakening
Refer to the magnetization curve below:
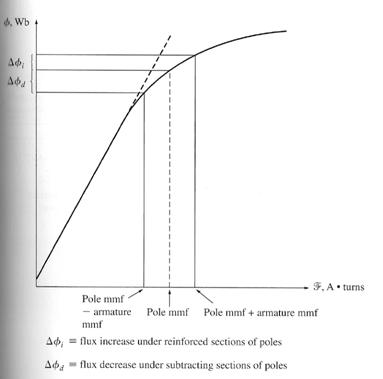
Most machine operate at flux densities near the saturation point. Therefore, at locations on the pole surfaces where the rotor mmf adds to the pole mmf, only a small increase in flux occurs. But at locations on the pole surfaces where the rotor mmf subtracts from the pole mmf, there is a larger decrease in flux. The net result is that the total average flux under the entire pole face is decreased.
The flux weakening causes problems in both generators and motors. In generators, the effect of flux weakening is simply to reduce the voltage supplied by the generator for any given load. In motors, the effect can be more serious. When the flux in a motor is decreased, its speed increases. But increasing the speed of a motor can increase its load, resulting in more flux weakening.
The flux and
mmf under the pole faces in a dc machine.
At those points where the mmf subtract, the flux closely follows the
net mmf in the iron; but at those points where the mmf add, saturation
limits the total flux present. Note also the neutral point of the rotor has
shifted.
L di/dt Voltages
The second major problem is the L di/dt voltage that occurs in commutator segments being shorted out by the brushes, sometimes called inductive kick.
The reversal
of current flow in a coil undergoing commutation. Note that the current in the coil between
segments a and b must reverse direction while the brush shorts together the
two commutator segments.
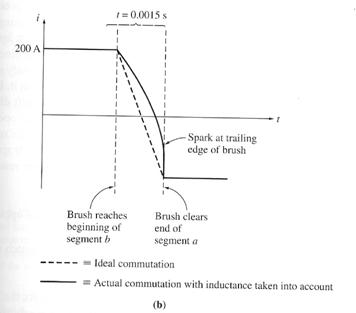
The current
reversal in the coil undergoing commutation as a function of time for both
ideal commutation and real commutation, with the coil inductance taken into
account.
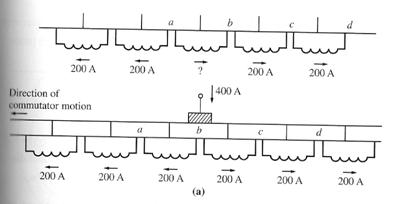
These figures represents a series of commutator segments and the conductors connected between them. Assuming that the current in the brush is 400A, the current in each path is 200A. Notice that when a commutator segment is shorted out, the current flow through that commutator segment must reverse. How fast must this reversal occur?
Assumming that the machine is turning at 800r/min and that there are 50 commutator segments, each commutator segment moves under a brush and clears it again in t=0.0015s. Therefore, the rate of change in current with respect to time in the shorted loop must average
![]()
With even a tiny inductance in the loop, a very significant inductive voltage kick v = L di/dt will be induced in the shorted commutator segment. This high voltage naturally causes sparking at the brushes of the machine, resulting in the same arcing problems that the neutral-plane shift causes.
Solutions to the Problems with Commutation
Three approaches have been developed to partially or completely correct the problems of armature reaction and L di/dt voltages:
- Brush Shifting
- Commutation poles or interpoles
- Compensating windings
Brush Shifting
The first attempts to improve the process of commutation in real dc machines started with attempts to stop the sparking at the brushes caused by the neutral-plane shifts and L di/dt effects.
The first approach taken by machine designers was simple: If the neutral plane of the machine shifts, why not shift the brushes with it in order to stop the sparking? This method is good but there are several problems:
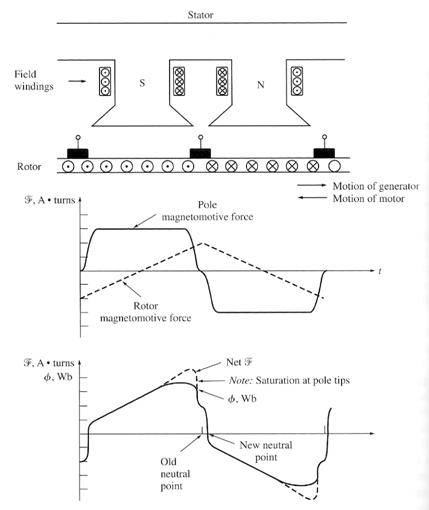
The neutral plane moves with every change in load, and the shift direction reverses when the machine goes from motor operation to generator operation. Therefore, someone has to adjust the brushes every time the load changed. Although this method may have stopped the brush sparking, it actually aggravated the flux-weakening effect of the armature reaction in the machine.
This is true because of 2 effects:
i) The rotor mmf now has a vector component that opposes the mmf from the poles.
ii) The change in armature current distribution causes the flux to bunch up even more at the saturated parts of the pole faces.
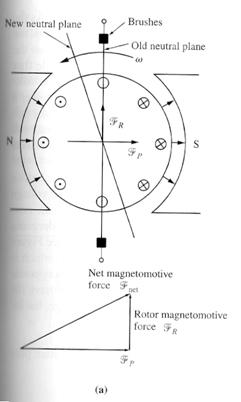
(b) The net
mmf in a dc machine with its brushes over the shifted neutral plane. Notice that now there is a component of
armature mmf directly opposing the poles' mmf and the net mmf in the
machine is reduced. (a) The net
mmf in a dc machine with its brushes in the vertical plane.
Commutation Poles or Interpoles
The basic idea here is that if the voltage in the wires undergoing commutation can be made zero, then there will be no sparking at the brushes. To accomplish this, small poles, called commutating poles or interpoles, are placed midway between the main poles. These commutating poles are located directly over the conductors being commutated. By providing a flux from the commutating poles, the voltage in the coils undergoing commutation can be exactly cancelled. If the cancellation is exact, then there will be no sparking at the brushes.
The commutating poles do not otherwise change the operation of the machine, because they are so small that they affect only the few conductors about to undergo commutation. Notice that the armature reaction under the main pole faces is unaffected, since the effects of the commutating poles do not extend that far. This means that the flux weakening in the machine is unaffected by commutating poles.
How is cancellation of the voltage in the commutator segments accomplished for all values of load? This is done by simply connecting the interpole windings in series with the windings on the rotor, as shown below:
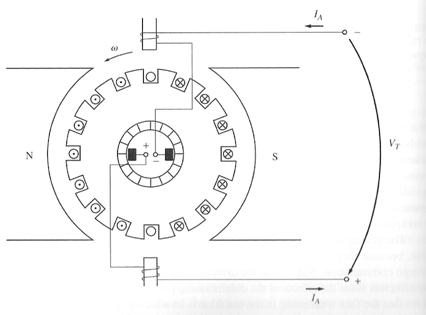
As the load increases, and the rotor current increases, the magnitude of the neutral-plane shift and the size of the L di/dt effects increase too. Both these effects increase the voltage in the conductors undergoing commutation.
However, the interpole flux increases too, producing a larger voltage in the conductors that opposes the voltage due to the neutral-plane shift. The net result is that their effects cancel over a broad range of loads. Note that interpoles work for both motor and generator operation, since when the machine changes from motor to generator, the current both in its rotor and in its interpoles reverses direction. Therefore, the voltage effects from them still cancel.
What polarity must the flux in the interpoles be?
The interpoles must induce a voltage in the conductors undergoing commutation that is opposite to the voltage caused by neutral-plane shift and L di/dt effects. In the case of a generator, the neutral plane shifts in the direction of rotation, meaning that the conductors undergoing commutation have the same polarity of voltage as the pole they just left.
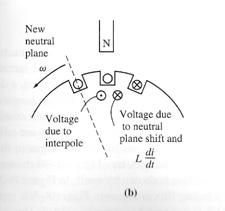
Determining the required polarity of an interpole. The flux from the interpole must produce a voltage that opposes the existing voltage in the conductor.
To oppose this voltage, the interpoles must have the opposite flux, which is the flux of the upcoming pole. In a motor, however, the neutral plane shifts opposite to the direction of rotation, and the conductors undergoing commutation have the same flux as the pole they are approaching. In order to oppose this voltage, the interpoles must have the same polarity as the previous main pole. Therefore,
- The interpoles must be of the same polarity as the next upcoming main pole in a generator.
- The interpoles must be of the same polarity as the previous main pole in a motor.
The use of commutating poles or interpoles is very common, because they correct the sparking problems of dc machines at a fairly low cost. They are almost always found in any dc machine of 1HP or larger.
It is important to realize that they do nothing for the flux distribution under the pole faces, so the flux-weakening problem is still present. Most medium-size, general-purpose motors correct for sparking problems with interpoles and just live with the flux-weakening effects.
Compensating Windings
For very heavy, severe duty cycle motors, the flux-weakening problem can be very serious. To completely cancel armature reaction and thus eliminate both neutral-plane shift and flux weakening, a different technique was developed.
This technique involves placing compensating windings in slots carved in the faces of the poles parallel to the rotor conductors, to cancel the distorting effect of armature reaction. These windings are connected in series with the rotor windings, so that whenever the load changes in the rotor, the current in the compensating windings changes too.
The figures below show the basic concept:
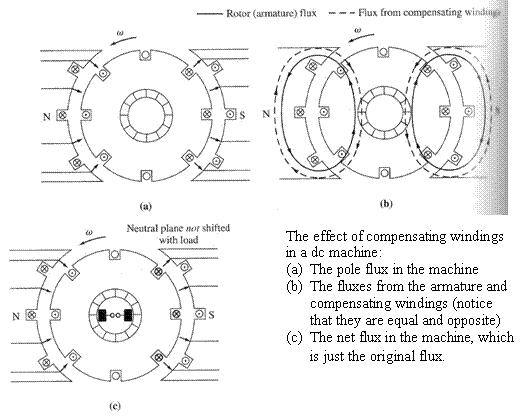
Another careful development of the effect of compensating windings on a dc machine is illustrated below:
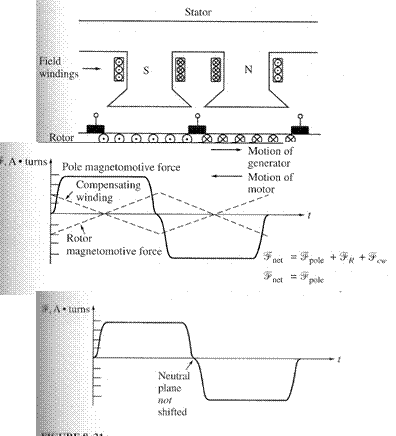
Notice that the mmf due to the compensating windings is equal and opposite to the mmf due to the rotor at every point under the pole faces. The resulting net mmf is just the mmf due to the poles, so the flux in the machine is unchanged regardless of the load on the machine.
The major disadvantage of compensating windings is that they are expensive, since they must be machined into the faces of the poles. Any motor that uses them must also have interpoles, since compensating windings do not cancel L di/dt effects. The interpoles do not have to be as strong, though since they are cancelling only L di/dt voltages in the windings, and not the voltages due to neutral-plane shifting. Because of the expense of having both compensating windings and interpoles on such a machine, these windings are used only where the extremely severe nature of a motor's duty demands them.
4. The Internal Generated Voltage and Induced Torque Equations of Real DC Machine
How can the voltage in the rotor windings of a real dc machine be determined?
The voltage out of the armature of a real dc machine is equal to the number of conductors per current path times the voltage on each conductor.
The voltage in any single conductor under the pole faces was previously shown to be eind = e = vBl
The voltage out of the armature of a real machine is thus:
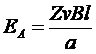
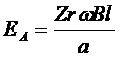 Where Z is the total number of conductors and a is the number of
current paths. The velocity of each
conductor in the rotor is v=r so,
Where Z is the total number of conductors and a is the number of
current paths. The velocity of each
conductor in the rotor is v=r so,
And with =BAP and A=2prl, and if there are P poles on the machine, then the total area A is
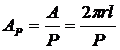
The total flux per pole in the machine:
![]()
Therefore, the internal generated voltage in the machine can be expressed as:
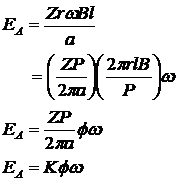
How much torque is induced in the armature of a real dc machine?
The torque on the armature of a real machine is equal to the number of conductors Z times the torque on each conductor. The torque in any single conductor under the pole faces was previously shown to be
tcond = r Icond lB
If there are a current paths in the machine, then the total armature current IA is split among the a current paths, so the current in a single conductor is given by
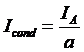
And the torque in a single conductor on the motor is:
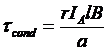
Since there are Z conductors, the total induced torque in a dc machine rotor is:
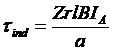
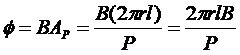 The flux per pole in this machine:
The flux per pole in this machine:
So the total induced torque is:
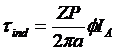
![]() Finally,
Finally,
5. The Construction of DC Machine
A simplified diagram of a dc machine:
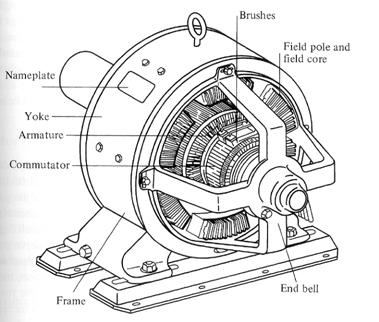
The physical structure of the machine consists of 2 parts: the stator and the rotor.
The stationary part consists of the frame, and the pole pieces, which project inward and provide a path for the magnetic flux. The ends of the pole pieces that are near the rotor spread out over the rotor surface to distribute its flux evenly over the rotor surface. These ends are called the pole shoes. The exposed surface of a pole shoe is called a pole face, and the distance between the pole face and the rotor is the air gap.
Two principal windings on a dc machine:
i- the armature windings: the windings in which a voltage is induced (rotor)
ii- the field windings: the windings that produce the main magnetic flux (stator)
Note: because the armature winding is located on the rotor, a dc machine's rotor is sometimes called an armature.
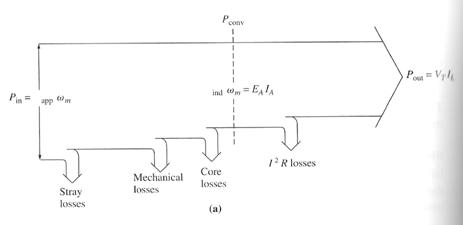
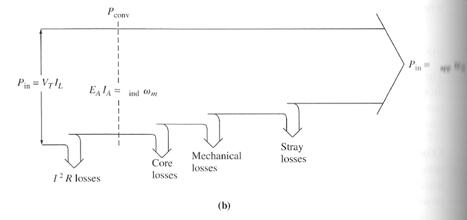
6. Power Flow and Losses in DC Machines
![]()
The Losses in DC Machine:
1. Electrical or Copper Losses (I2R Loss)
Armature loss: PA = IA2 RA
Field loss: PF = IF2 RF
2. Brush Losses
PBD = VBD2 IA
3. Core Losses
- Hysteresis and Eddy Current Loss
4. Mechanical Losses
- Friction and windage loss
5. Stray Loss
The Power-Flow Diagram:
Generator Motor
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||