| Afaceri | Agricultura | Comunicare | Constructii | Contabilitate | Contracte |
| Economie | Finante | Management | Marketing | Transporturi |
Electrica
|
|
Qdidactic » bani & cariera » constructii » electrica Studiul campurilor electrice laplaciene - consideratii teoretice |
Studiul campurilor electrice laplaciene - consideratii teoretice
1. Scopul lucrarii este determinarea experimentala a spectrului campului electric laplacian plan-paralel prin modelarea cu o retea analizoare de tip R, precum si analiza campului electric printr-o metoda numerica asistata de calculator.
2. Consideratii teoretice:
Pentru rezolvarea unor probleme de camp mai complexe, adica configuratii
complicate, neomogenitati etc., este mai avantajos sa se aplice o metoda numerica si anume metoda diferentelor finite sau metoda elementelor finite. Acestea sunt metode aproximative, aplicarea lor ducand la rezolvarea unor sisteme de ecuatii algebrice si nu a unor ecuatii cu derivate partiale.
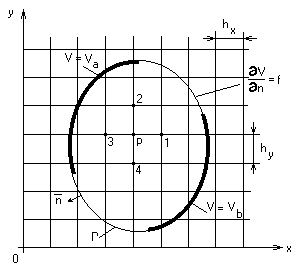
Rezolvarea problemei de camp intr-un domeniu limitat de curba G, situat intr-un plan xoy (fig.1), inseamna rezolvarea ecuatiei diferentiale (1) care descrie un camp electric laplacian plan-paralel.
![]()
|
Fig.1 |
Solutia ecuatiei (1) trebuie sa verifice si conditiile de frontiera.
Conditiile de frontiera ale domeniului considerat sunt:
- de tip Dirichlet, daca se cunosc valorile functiei potential;
- de tip Neumann, daca se cunoaste derivata potentialului
dupa normala ![]() .
.
In planul xoy se considera doua familii de drepte, care formeaza o retea ortogonala, numita retea de discretizare, intersectia dreptelor fiind nodurile retelei. Nodurile retelei pot fi noduri interioare, sau de frontiera, in functie de pozitia acestora in domeniul considerat. Distanta dintre doua noduri vecine se numeste pasul retelei, atat pe verticala (hy) cat si pe orizontala (hx). Daca pasul pe orizontala nu este constant si difera de cel de pe verticala, reteaua se numeste cu pas variabil. Daca pasul pe orizontala difera de pasul de pe verticala reteaua este dreptunghiulara, iar daca pasul pe verticala este egal cu pasul pe orizontala, reteaua este patratica (hx = hy = h).
In interiorul domeniului limitat de curba G (fig.1) s-a considerat un nod p si patru noduri vecine acestuia. Aplicand metoda diferentelor finite, se vor determina valorile functiei potential V intr-un numar finit de puncte-noduri ale retelei de discretizare. Astfel, daca se exprima potentialele nodurilor vecine lui p printr-o dezvoltare in serie Taylor, limitandu-ne la termenii de ordinul doi (eroarea fiind mica daca pasul retelei este mic) se obtin:
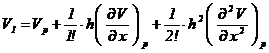 (
(
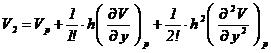
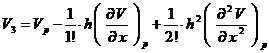
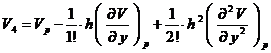
Adunand cele patru relatii se obtine:
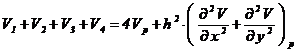 (
(
in care
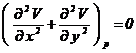 rezulta
rezulta
![]() (
(
care este o ecuatie echivalenta cu (1), dar exprimata in diferente finite.
In cadrul metodei diferentelor
finite, se scriu ecuatii de forma (7) pentru toate nodurile interioare
si ecuatii pentru nodurile de frontiera cu potential
necunoscut (conditii Neumann), rezultand un sistem de n ecuatii cu n
necunoscute, ale carui solutii sunt valorile potentialelor V in
noduri. Cunoscand aceste valori se pot determina si alte marimi, de
exemplu vectorul camp electric ![]() .
.
Scazand relatia ( din (2) se obtine derivata de ordinul intai dupa x in punctul p:
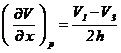
si scazand relatia (5) din (3) se obtine derivata de ordinul intai dupa y in p:
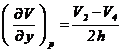
Astfel, vectorul camp electric va fi:
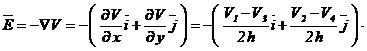 (
(
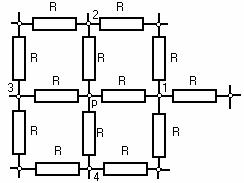
Pentru determinarea potentialelor din nodurile retelei de discretizare se poate folosi un model de retea cu rezistente electrice (fig.2), realizat prin conectarea unor rezistente electrice intre fiecare nod al retelei de discretizare si asigurand aceeasi geometrie a frontierei, respectiv aceleasi conditii de frontiera.
In nodul p se scrie ecuatia corespunzatoare metodei potentialelor la noduri
![]() (
(
adica
![]() (
(
ecuatie identica cu (7), in care potentialele nodurilor pot fi masurate pe modelul de retea..
|
Fig.2 Model de retea cu rezistente electrice |
3. Partea experimentala
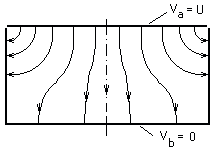
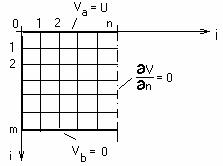
3.1. Se considera doi electrozi (de lungime mare) avand intr-o sectiune transversala forma din figura 3 si datorita simetriei fata de planul median, se studiaza campul in jumatate din domeniu (fig.4) in care intervin conditii de tip Neumann. Cei doi electrozi se obtin prin realizarea unor legaturi echipotentiale intre nodurile unui model de retea cu rezistente, ca-n figura 2. Electrozii se conecteaza la o sursa de tensiune continua (Va – Vb = U = 10 V).
|
Fig.3 Fig.4 |
3.2. Cu un voltmetru numeric se masoara potentialele nodurilor domeniului si se trec in tabelul 1.
Tabelul 1
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3. Valorile potentialelor masurate se reprezinta pe hartie milimetrica la scara si se traseaza liniile echipotentiale pentru 2, 4, 6, 8 Volti, pozitiile punctelor de un anumit potential obtinandu-se prin interpolare.
3.4. Perpendicular pe liniile echipotentiale, se traseaza liniile de camp electric, astfel incat sa formeze figuri geometrice asemenea.
4. Simulare asistata de calculator
Rezultatele obtinute pe cale experimentala se compara cu cele obtinute prin simulare cu ajutorul unui program realizat pe baza metodei elementelor finite numit QUICK FIELD.
Pasii de lucru
1. Denumirea problemei: Din meniul FILE se deschide un nou fisier (NEW), QUICK FIELD PROBLEM si se atribuie un nume problemei;
2. Se defineste tipul problemei: PROBLEM TYPE ELECTROSTATICS, precum si tipul configuratiei PLANE - PARALLEL (xy) si gradul de precizie NORMAL;
3. Se stabilesc unitatile de masura: LENGTH UNITS MILIMETERS si sistemul de coordonate, CARTESIAN COORDINATES;
4. Crearea modelului geometric: GEOMETRY (2click)
- se definesc varfurile geometriei: INSERT VERTICES
- se traseaza laturi: INSERT EDGES
- se definesc blocuri (marginite de laturi): SELECT OBJECTS BLOCKS si se eticheteaza (se denumesc) LABEL
- se definesc laturi (frontiera domeniului): SELECT OBJECTS EDGES si se eticheteaza LABEL (pentru conditiile de tip Dirichlet si pentru cele de tip Neumann);
5. Discretizarea domeniului: Se realizeaza reteaua de discretizare din meniul BUILD MESH. Programul permite alegerea unei retele mai dese in zona de interes printr-un numar mic de SPACING ceea ce corespunde unei retele cu mai multe noduri, deci elemente finite mai multe (2click pe varfurile geometriei, SPACING MANUAL);
6. Precizarea datelor de intrare: Apeland DATA se introduc elementele necesare pentru definirea elementelor ce au fost etichetate. Se rezolva problema SOLVE si in acelasi timp se salveaza;
7. Analizarea rezultatelor: Programul permite vizualizarea liniilor echipotentiale, a liniilor de camp electric, apeland meniul VIEW FIELD PICTURE, precum si a altor marimi (LOCAL VALUES), din domeniul considerat.
5.Concluzii:
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |