
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Curentul electric: Intensitatea, densitatea curentului electric - purtatorii de sarcina |
Curentul electric: Intensitatea, densitatea curentului electric - purtatorii de sarcina
CURS fizica
1. Curentul electric
2. Intensitatea curentului electric
3. Densitatea de curent
4. Purtatorii de sarcina in metale
5. Legea lui Ohm
6. Benzi de energie. Conductori. Semiconductori. Izolatori
7. Circuite de curent continuu
8. Aplicarea legii lui Ohm
9. Circuite electrice ramificate. Legile lui Kirchoff
1. Curentul electric
Definitie: Miscarea ordonata a purtatorilor de sarcina electric se numeste curent electric.
Curentul electric poate sa fie:
De conductie - Daca miscarea ordonata a sarcinilor electrice are loc in medii conductoare sau in vid. De exemplu:
i. Miscarea ordonata a electronilor liberi in metale.
ii. Miscarea electronilor de la catod la anod in tuburi electronice.
iii. Miscarea ordonata a ionilor in electroliti
iv. Miscarea ordonata a ionilor si electronilor in gazele ionizate.
De convectie - Daca miscarea ordonata a sarcinilor electrice de pe un corp incarcat electric are loc impreuna cu acel corp.
Miscarea ordonata a sarcinilor electrice (curentul de conductie) apare in prezenta unui camp electric. Sensul curentului electric coincide cu sensul campului electric din conductor si este acelasi cu sensul deplasarii sarcinilor electrice pozitive.
2. Intensitatea curentului electric
Definitie: Intensitatea curentului printr-un conductor este egala cu sarcina electric transportata de purtatorii de sarcina in unitatea de timp, prin orice sectiune transversala a conductorului.
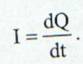
(1)
Unitatea de masura pentru
intensitatea curentului electric este
Amperul.
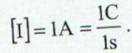
(2)
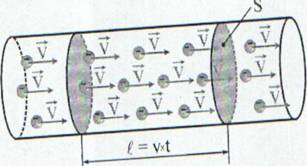
Fig. 1 Electronii, purtatorii de sarcina din
conductorii strabat suprafata S in timpul t.
3. Densitatea de curent
Intensitatea curentului electric poate caracteriza complet modul in care este condus curentul electric numai prin conductorii omogeni si rectilinii pentru care viteza purtatorilor de sarcina este aceeasi in orice sectiune a conductorului. Pentru un corp cu sectiune variabila, pentru a descrie miscarea purtatorilor de sarcini electrice, trebuie introdusa o alta marime fizica, densitatea de curent. Fie n concentratia purtatorilor de sarcina.
![]()
(3)
Fiecare purtator are sarcina electrica egala cu q si viteza v. In timpul t vor trece prin sectiunea S toti purtatorii din cilindrul cu generatoarea:
![]()
Sarcina totala, Q este:
Q = N ∙ q (5)
Din ecuatia (3) numarul total de purtatori este:
N = n ∙ V = n ∙ (S ∙ l) = n ∙ (S ∙ v ∙ t) (6)
N = n ∙ v ∙ t ∙ S
De aici sarcina electrica totala este:
Q = q ∙ n ∙ v ∙ t ∙ S. (7)
Intensitatea curentului devine:
![]()
(8)
Iar densitatea de curent care este curentul electric care revine unitatii din suprafata sectiunii conductorului:
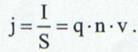
(9)
Densitatea de curent electric este o marime vectoriala:
![]()
(10)
Pentru a obtine din ecuatia (10) expresia intensitatii curentului electric trebuie sa folosim un element de suprafata orientat.
![]()
(11)
Daca conductorul nu este omogen atunci se poate define un element infinitesimal de curent electric care trece printr-un element infinitesimal de suprafata pentru care densitatea de curent se poate considera constanta:
|
![]()
(12)
Iar intensitatea curentului electric prin toata suprafata este:
![]()
(13)
4. Purtatorii de sarcina in metale
Modelul clasic al conductiei electrice in metale a fost elaborate la inceputul secolului trecut de catre P.Drude si H. A. Lorentz¹. Conform modelului Drude-Lorentz reteaua cristalina din metale este format din ioni
pozitivi.
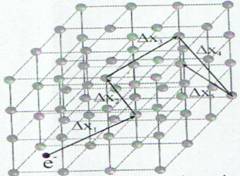 Electronii liberi,
fostii electroni de valen-
Electronii liberi,
fostii electroni de valen-
ta se afla intr-o permanent miscare termica,
haotica
cu viteza termica medie ![]() .
.
Comportarea electronilor liberi in metale
este analoga cu comportarea moleculelor
unui gaz ideal, deci se pot aplica legile ga-
zelor.
Fig. 2 Electronii liberi in miscarea lor
se ciocnesc cu atomii din nodurile retelei.
5. Legea lui Ohm
Modelul gazului electronic ne permite sa justificam legea lui Ohm pe cale teoretica. In metale si semiconductori miscarea ordonata a purtatorilor de sarcina este ingreunata (apare o rezistenta la trecerea curentului electric) de ciocnirea lor cu ionii retelei cristaline. In urma acestor ciocniri viteza in curent a electronilor se anuleaza. Ciocnirile electronilor cu ionii au un caracter electric este E. Atunci asupra electronilor actioneaza forta:
![]()
(14)
De aici se observa ca electronii sunt accelerati pe durata parcursului liber dintre doua ciocniri succesive:
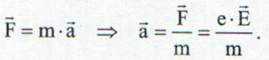
(15)
Intr-un interval de timp ∆t dintre doua ciocniri succesive electronul parcurge distanta ∆x
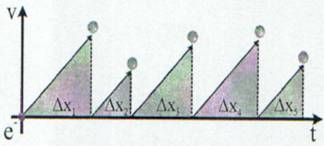
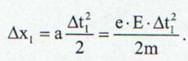
(16)
Intr-un interval de timp ∆t
dintre urmatoarele doua ciocniri
succesive electronul parcurge
distanta ∆x
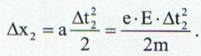 Fig. 3 Prin ciocnirea electronilor cu
atomii din
Fig. 3 Prin ciocnirea electronilor cu
atomii din
nodurile retelei cristaline viteza scade la zero.
In intervalul de timp t electronul parcurge distanta x:
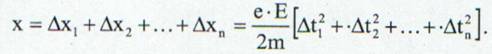
(18)
![]()
Hendrick A. Lorentz (1853-1928) fizician olandez a castigat premiul Nobel pentru fizica in anul 1902. A dezvoltat teoria electromagnetica a luminii, a introdus notiunea de electron ca constituent al materiei. A formulat o teorie consistenta a electricitatii, magnetismului si a luminii. Prin cercetarile sale a ajutat la explicarea efectului Zeeman, despicarea liniilor spectrale atunci cand o unda electromagnetica strabate un camp magnetic.
Viteza medie a miscarii electronului este:
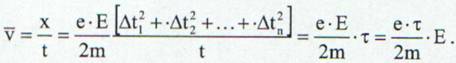
(19)
unde cu τ s-a notat timpul mediu dintre doua ciocniri si care se mai numeste si timpul liber mediu:
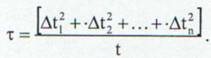
(20)
Daca consideram din nou intensitatea campului electric ca si vector obtinem forma locala a legii lui Ohm:
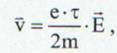
(21)
iar densitatea de curent electric este atunci:
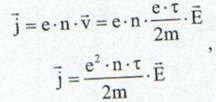
(22)
sau introducand conductivitatea electrica, σ:
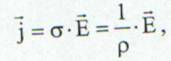
(23)
cu:
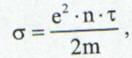
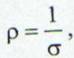 si:
si:
(25)
rezistivitatea electrica.
Ecuatia (22) reprezinta forma locala (sau diferentiala) a legii lui Ohm. Conductivitatea electrica, si rezistivitatea electrica (care este inversul conductivitatii electrice) sunt marimi fizice constante pentru un material dat, a caror valoare depinde prin intermediul lui n si de natura materialului.
Legea lui Ohm pentru o portiune de circuit
Daca consideram o portiune de conductor atunci se poate defini o cadere de tensiune la capetele acestuia data de relatia:
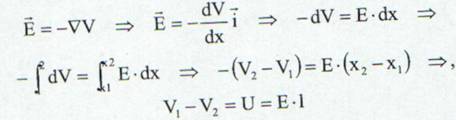
de unde intensitatea campului electric este:
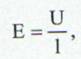
(27)
de unde densitatea de curent este:
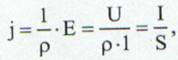
(28)
deci intensitatea curentului electric este:
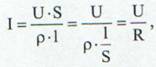
(29)
unde s-a notat prin R rezistenta electrica:
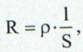
(30)
deci legea lui Ohm pentru o portiune de conductor se poate scrie simplu:
![]()
(29a)
Definitie: Rezistenta electrica a unei portiuni de conductor este direct proportionala cu lungimea conductorului, si invers proportionala cu aria sectiunii transversale a conductorului si depinde (prin ρ) de natura materialului conductorului.
Unitatea de masura a rezistentei este Ohmul:
![]()
(31)
Definitie: Rezistivitatea electrica a unui conductor este rezistenta electrica a unei portiuni din acel conductor de lungime 1m si aria sectiunii transversale de 1m
Dependenta de temperatura a rezistivitatii electrice
Ionii pozitivi din nodurile retelei cristaline executa la orice temperatura oscilatii in jurul pozitiei de echilibru. Cu cresterea temperaturii creste si amplitudinea oscilatiilor ionilor ceea ce determina cresterea probabilitatii de ciocnire a electronilor cu acestea.
![]()
(32)
unde ρ este rezistivitatea conductorului la temperatura de 0° C. Factorul α se numeste coeficientul de temperatura al rezistivitatii. In mod similar se poate obtine o relatie similara si pentru rezistenta:
![]()
6. Benzi de energie in solide. Conductori. Semiconductori. Izolatori
In atomii izolati, electronii se gasesc pe nivele energetice discrete. In concordanta cu principiul lui Pauli in atom nu pot exista doi electroni care au toate cele 4 numere cuantice egale. Consideram un proces in care N atomi individuali se apropie pentru a forma un cristal. Prin apropiere cei N atomi intra in interactiune si formeaza un sistem cuantic - cristalul. La ocuparea nivelelor energetice ale atomilor din cristal, principiul lui Pauli trebuie respectat pentru intreg cristalul si nu pentru atomii individuali.La formarea cristalului nivelele energetice identice ale diferitilor atomi este necesar sa se deplaseze in sus si in jos pe scara energiilor astfel incat in cristal sa nu existe doi atomi ale caror energii sa aiba aceeasi valoare.
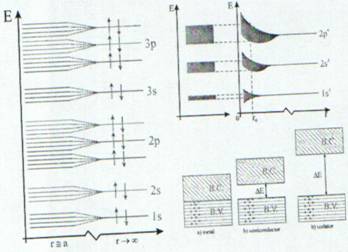
Fig.4 Nivelele energetice ale
electronilor atomilor izolati for-
meaza benzi de energie la apro-
pierea lor (stanga). Aranjarea pe
benzi si umplerea lor cu electroni
(dreapta).
7. Circuite de curent continuu
Circuite electrice neramificate
Cel mai simplu circuit este format dintr-un generator (sursa de tensiune) si un consummator (o rezistenta) legate in serie cu ajutorul unor sarme conductoare a caror rezistenta se presupune neglijabila.
Elemente de circuit:
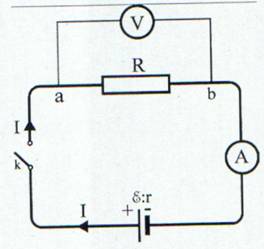 Generatorul - caracterizat prin:
Generatorul - caracterizat prin:
tensiunea electromotoare
rezistenta interna.
● Rezistorul - caracterizat prin valoarea rezistentei.
● Aparate de masura - caracterizate prin:
1. rezistenta interna.
2. valoarea maxima a marimii masurate.
3. Sensibilitatea aparatului - numa-
rul de diviziuni cu care este dotat apara-
Fig. 5 Exemplu de circuit electric tul pe o scara circulara cu raza de 1m, cand valoarea masurata este egala cu unitatea.
8. Aplicarea legii lui Ohm
Daca consideram caderea de tensiune, Uab intre punctele a si b din figura atunci intre marimile Uab, R si I exista urmatoarele relatii:
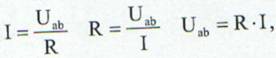
(34)
legea lui Ohm pentru o portiune de circuit.
Daca in schimb dorim sa studiem intreg circuitul atunci trebuie sa scriem legea lui Ohm sub forma:
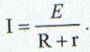
(35)
Fie n - numarul rezistoarelor din circuit si m - numarul surselor din circuit atunci legea lui Ohm pentru intreg circuitul este data de:
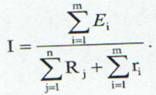
(36)
9. Circuite electrice ramificate. Legile lui Kirchhoff
Legea I a lui Kirchhoff
Enunt: Suma algebrica a intensitatii curentilor electrici care se intalnesc intr-un nod de retea este egala cu zero.
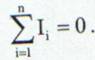
(37)
Legea I a lui Kirchhoff este o consecinta a conservarii sarcinii electrice. Sarcina electrica care intra intr-un nod in timpul t este egala cu sarcina electrica care iese din nod in acelasi timp t.
Legea II - a a lui Kirchhoff
Enunt: De-a lungul conturului unui ochi de retea suma algebrica a tensiunilor electromotoare este egala cu suma algebrica a produselor dintre intensitatea curentului electric si rezistenta totala din fiecare ramura.
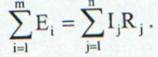
(38)
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








