
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Continuitatea unei functii pe o multime |
Continuitatea unei functii pe o multime
CONTINUITATEA UNEI FUNCTII PE O MULTIME
Definitie : Se spune ca o functie f:E→R este continua pe o multime A![]() E daca este continua in fiecare punct din A.
E daca este continua in fiecare punct din A.
Daca o functie este continua pe tot domeniul ei de definitie E , se spune , mai simplu , ca este continua (fara alta specificare asupra multimii pe care are aceasta proprietate) .
Functiile elementare sunt continue :
Daca P(x) este un polinom , avem :
![]() P(x) = P(X X
P(x) = P(X X ![]() R
R
Daca f(x)
=![]() este o functie rationala si daca
este o functie rationala si daca ![]() avem :
avem :
![]()
![]()
![]()
![]() si
si ![]()
![]() (
(![]() >0).
>0).
![]()
![]() si
si ![]()
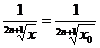 ,
, ![]() .
.
![]()
![]() ,
, ![]() ,
, ![]() >0 ) si
>0 ) si ![]()
![]() , (
, (![]() >0 ,
>0 , ![]() ) .
) .
![]()
![]() , (
, ( ![]() > 0 ) .
> 0 ) .
![]()
![]() , (
, ( ![]() > 0 ,
> 0 , ![]() ,
, ![]() > 0 ) .
> 0 ) .
![]()
![]() ,
, ![]()
![]() , (
, ( ![]() )
)
![]()
![]() , (
, ( 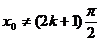 , k intreg ) ,
, k intreg ) ,
![]()
![]() , (
, ( ![]() , k intreg ) .
, k intreg ) .
![]()
![]() si
si ![]()
![]() , (
, ( ![]() )
)
![]()
![]() si
si ![]()
![]() , (
, ( ![]() ) .
) .
Asadar , polinoamele , functiile rationale , functia radical , functia putere , functia exponentiala , functia logaritmica , functiile circulare directe si functiile circulare reciproce sunt continue ( pe tot domeniul lor de definitie ) .
Se va vedea mai departe ca si celelalte functii elementare ( care se ob
DERIVATA UNEI FUNCTII RECIPROCE
Fie I si J doua intervale oarecare . Fie f : I→J o aplicatie bijectiva
strict monotona si ![]() aplicatia reciproca .
Se poate demonstra .
aplicatia reciproca .
Se poate demonstra .
TEOREMA
Daca f este derivabila intr-un punct x ![]() I si daca derivata sa nu se anuleaza in acest punct , f'(x) ≠ 0 , atunci functia
reciproca
I si daca derivata sa nu se anuleaza in acest punct , f'(x) ≠ 0 , atunci functia
reciproca ![]() este derivabila in
punctul corespunzator y = f (x)
si
este derivabila in
punctul corespunzator y = f (x)
si
|
|
Justificarea geometrica a acestei teoreme este urmatoarea :
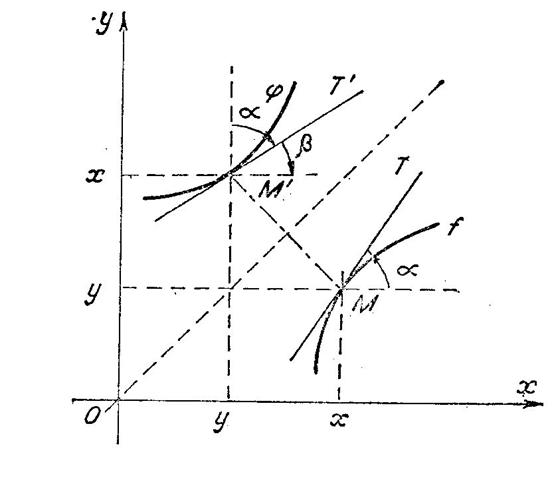
Graficele functiilor f si ![]() sunt simetrice fata de
prima bisectoare . Deoarece functia f
este derivabila in punctul x , graficul sau admite in punctul ( x , y ) tangenta , MT , neparalela
sunt simetrice fata de
prima bisectoare . Deoarece functia f
este derivabila in punctul x , graficul sau admite in punctul ( x , y ) tangenta , MT , neparalela![]() cu axa Ox ( deoarece tg
cu axa Ox ( deoarece tg![]() ) ; urmeaza ca si graficul functiei reciproce
) ; urmeaza ca si graficul functiei reciproce ![]() admite in punctul
corespunzator ( y , x ) tangenta , M' T' , neparalela cu axa Oy deci este derivabila in punctul y .
admite in punctul
corespunzator ( y , x ) tangenta , M' T' , neparalela cu axa Oy deci este derivabila in punctul y .
Deoarece ![]() , avem
, avem ![]() dar
dar ![]() si
si ![]() sunt repectiv
coeficientii unghiulari
sunt repectiv
coeficientii unghiulari ![]() si f'(x) ai celor doua tangente , deci
si f'(x) ai celor doua tangente , deci ![]() .
.
TABLOUL DERIVATELOR UNOR FUNCTII ELEMENTARE
|
Functia f |
Derivata f' |
Multimea pe care f' este derivabila |
|
c , (constant) |
|
R |
|
x |
|
R |
|
|
|
R |
|
|
|
|
|
|
|
[ 0 ,+∞ ) |
|
|
|
( 0 ,+∞ ) |
|
|
|
( 0 ,+∞ ) |
|
sin x |
cos x |
R |
|
cos x |
- sin x |
R |
|
tg x |
|
|
|
ctg x |
- |
x ≠ k |
|
arcsin x |
|
|
|
arccos x |
|
|
|
arctg x |
|
R |
|
arcctg x |
- |
R |
|
|
|
R |
|
|
|
R |
|
ln x |
|
( 0 ,+∞ ) |
|
|
|
( 0 ,+∞ ) |
|
|
|
|
|
Nr. Crt. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Analize pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








