
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Functia de repartitie si densitatea de probabilitate |
Functia de repartitie si densitatea de probabilitate
1 Functia de repartitie
Definitia 1.1
Functia ![]() se
numeste functie de repartitie daca;
se
numeste functie de repartitie daca;
i) F este monoton crescatoare,
ii) F este continua la stinga,
iii)
![]() si
si ![]()
Exemplu : Plecand de la functia arctg :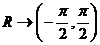 , care este continua si monoton crescatoare pe
, care este continua si monoton crescatoare pe
![]() , putem construi urmatoarea functie
, putem construi urmatoarea functie ![]() , care verifica conditiile din definitia 6.1.1
si este continua pe toata axa reala.
, care verifica conditiile din definitia 6.1.1
si este continua pe toata axa reala.
Teorema
1.1 Pentru orice functie de repartitie ![]() au
loc urmatoarele proprietati:
au
loc urmatoarele proprietati:
i)
pentru orice ![]() exista si este finita
exista si este finita ![]() , unde cu
, unde cu ![]() am
notat limita la dreapta in punctul x al functiei
am
notat limita la dreapta in punctul x al functiei ![]()
ii)
F este continua in punctul ![]() daca si numai daca
daca si numai daca ![]() , altfel in punctul x avem o
discontinuitate de speta intai ( adica exista limitele laterale
in x si sunt finite).
, altfel in punctul x avem o
discontinuitate de speta intai ( adica exista limitele laterale
in x si sunt finite).
iii) multimea punctelor de discontinuitate ale functiei de reapartitie F este cel mult numarabila.
2 Functia de repartitie a unei variabile aleatoare reale
Fie ![]() o
o ![]() -algebra de evenimente,
-algebra de evenimente, ![]() evenimentul sigur ,
evenimentul sigur , ![]() o
probabilitate
o
probabilitate ![]() -aditiva , iar
-aditiva , iar ![]() o
variabila aleatoare reala. Se defineste o functie
o
variabila aleatoare reala. Se defineste o functie ![]() data prin formula
data prin formula
![]()
pentru orice ![]()
Teorema 2.2 Daca ![]() este o variabila aleatoare reala, iar
este o variabila aleatoare reala, iar
![]() functia de repartitie
corespunzatoare data de relatia (7.1) atunci urmatoarele
afirmatii sunt echivalente:
functia de repartitie
corespunzatoare data de relatia (7.1) atunci urmatoarele
afirmatii sunt echivalente:
i)
F este continua la dreapta in ![]()
|
ii)
![]() .
.
Demonstratie Se
considera sirul ![]() strict monoton
descrescator,
strict monoton
descrescator, ![]() astfel incat
astfel incat ![]() . Avem :
. Avem :
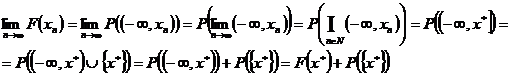
Prin urmare , daca F este
continua la dreapta in x , avem ![]() , deci
, deci ![]() , si invers.
, si invers.
3 Functia densitate de probabilitate
Definitia 3.1 O
functie ![]() integrabila in sens Riemann se
numeste densitate de probabilitate, daca verifica :
integrabila in sens Riemann se
numeste densitate de probabilitate, daca verifica :
i) ![]() pentru orice
pentru orice ![]()
ii) ![]()
Teorema 3.1 Daca ![]() este o densitate de probabilitate, atunci
functia
este o densitate de probabilitate, atunci
functia ![]() va
fi o functie de repartitie.
va
fi o functie de repartitie.
Observatie Daca ![]() este o densitate de probabilitate atunci
functia de repartitie F este chiar continua.
este o densitate de probabilitate atunci
functia de repartitie F este chiar continua.
Teorema 3.2 Daca
densitatea de probabilitate ![]() este continua in punctul
este continua in punctul ![]() , atunci functia de repartitie
, atunci functia de repartitie ![]() , data de formula
, data de formula ![]() este derivabila in punctul
este derivabila in punctul ![]()
Demonstratie
Fie ![]() un sir monoton
crescator de numere reale astfel incat
un sir monoton
crescator de numere reale astfel incat ![]() pentru orice
pentru orice ![]() si
si
![]() . Atunci:
. Atunci:
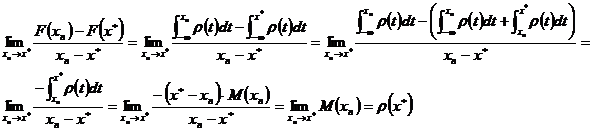 Astfel am demonstrat ca F este derivabila la stinga
in punctual
Astfel am demonstrat ca F este derivabila la stinga
in punctual ![]() si
si
![]() . In mod analog se demonstreaza ca F este
derivabila la dreapta in punctul
. In mod analog se demonstreaza ca F este
derivabila la dreapta in punctul ![]() .Prin urmare, pentru
orice punct de continuitate
.Prin urmare, pentru
orice punct de continuitate ![]() a lui
a lui
![]() , F este
derivabila in
, F este
derivabila in ![]() si
si ![]() .
.
Observatie Daca densitatea de probabilitate ![]() este continua pe axa reala, atunci
functia de repartitie corespunzatoare F este derivabila pe
axa reala si
este continua pe axa reala, atunci
functia de repartitie corespunzatoare F este derivabila pe
axa reala si ![]()
![]() . Prin urmare in cazul
densitatilor de probabilitate continue
. Prin urmare in cazul
densitatilor de probabilitate continue ![]() functia de repartitie F joaca
rolul de primitiva a lui
functia de repartitie F joaca
rolul de primitiva a lui ![]()
Teorema 3.3 Daca ![]() este o densitate de probabilitate, atunci functia
de repartitie
este o densitate de probabilitate, atunci functia
de repartitie ![]() data de formula
data de formula ![]() este o functie absolut continua.
este o functie absolut continua.
Demonstratie Trebuie
sa demonstram ca pentru orice ![]() exista
exista ![]() astfel incat pentru orice
astfel incat pentru orice ![]() si orice puncte
si orice puncte ![]() cu
cu ![]() rezulta ca
rezulta ca ![]() . Intr+adevar, pentru un
. Intr+adevar, pentru un ![]() dat
alegem
dat
alegem ![]() , unde
, unde ![]() este o margine pentru functia
integrabila Riemann :
este o margine pentru functia
integrabila Riemann :
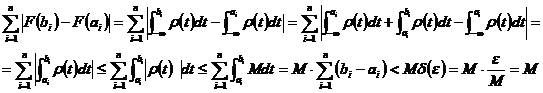
Teorema
3.4 Daca o functie de repartitie ![]() este absolute continua atunci exista
o densitate de probabilitate
este absolute continua atunci exista
o densitate de probabilitate ![]() astfel incit
astfel incit ![]() pentru orice
pentru orice ![]()
4 Functia de repartitie a unui vector aleator real
n-dimensional
Fie ![]() o
o ![]() -algebra de evenimente avand pe
-algebra de evenimente avand pe ![]() evenimentul sigur, iar
evenimentul sigur, iar ![]()
![]() un
vector aleator, iar
un
vector aleator, iar ![]() o
probabilitate data.
o
probabilitate data.
Definitia 4.1
Functia ![]() data prin formula
data prin formula ![]() pentru orice
pentru orice ![]() se
numeste functia de repartitie a vectorului aleator X.
se
numeste functia de repartitie a vectorului aleator X.
Teorema 4.1 Are loc
urmatoarea egalitate pentru orice numere reale ![]() cu
cu![]()
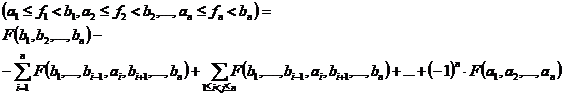 Teorema
4.2 Daca F este o functie de repartitie a unui vector
aleator real n dimensional, atunci
Teorema
4.2 Daca F este o functie de repartitie a unui vector
aleator real n dimensional, atunci
![]()
unde ![]() este o functie de repartitie a unui
vector aleator real n-1 dimensional.
este o functie de repartitie a unui
vector aleator real n-1 dimensional.
Teorema 4.3 Daca F este o functie de repartitie a unui vector aleator real n dimensional, atunci :
![]() .
.
Definitia 4.2 O
functie ![]() integrabila Riemann se numeste
densitate de probabilitate, daca verifica:
integrabila Riemann se numeste
densitate de probabilitate, daca verifica:
i) ![]() pentru
orice
pentru
orice ![]() ;
;
ii)
![]() .
.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Proiecte pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








