
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Tipuri de convergenta ale sirurilor de variabile aleatoare reale |
Tipuri de convergenta ale sirurilor de variabile aleatoare reale
1. Siruri de variabile aleatoare reale
Fie ![]() o
o ![]() algebra
de evenimente cu
algebra
de evenimente cu ![]() evenimentul
sigur , iar
evenimentul
sigur , iar ![]() multimea tuturor
variabilelor aleatoare reale definite pe
multimea tuturor
variabilelor aleatoare reale definite pe ![]() cu valori reale :
cu valori reale : ![]() este variabila
aleatoare reala . In continuare avem sa definim notiunea de
sir de variabile aleatoare reale:
este variabila
aleatoare reala . In continuare avem sa definim notiunea de
sir de variabile aleatoare reale:
Definitia
1.1. O functie ![]() se numeste un
sir de variabile aleatoare reale.
se numeste un
sir de variabile aleatoare reale.
2. Convergenta punctuala si uniforma a sirurilor de variabile aleatoare reale
Definitia
2.1. Vom spune ca un sir de variabile aleatoare reale ![]() converge punctual catre o functie
converge punctual catre o functie ![]() daca pentru orice
daca pentru orice ![]() avem
avem ![]() , adica daca pentru orice
, adica daca pentru orice ![]() sirul
sirul ![]() este un sir de
numere reale convergent catre un numar real, limita pe care o
notam cu
este un sir de
numere reale convergent catre un numar real, limita pe care o
notam cu ![]() .
.
Folosim
formalismul matematic sirul de variabile aleatoare reale converge punctual
catre functia ![]() daca pentru
orice
daca pentru
orice ![]() si pentru
orice
si pentru
orice ![]() exista
exista ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() sa avem
sa avem ![]() .
.
Definitia
2.2. Vom spune ca sirul de variabile aleatoare reale ![]() este marginit punctual, daca pentru orice
este marginit punctual, daca pentru orice ![]() avem ca multimea de numere reale
avem ca multimea de numere reale ![]() este o multime marginita, adica pentru
fiecare
este o multime marginita, adica pentru
fiecare ![]() exista
exista ![]() astfel incat
astfel incat 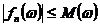 .
.
Teorema
2.1. Fie ![]() un sir de variabile aleatoare reale marginit
punctual .
un sir de variabile aleatoare reale marginit
punctual .
Atunci functiile:
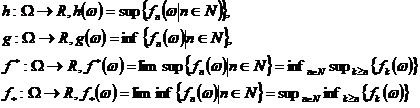
definite
pentru orice ![]() sunt tot variabile aleatoare reale.
sunt tot variabile aleatoare reale.
Teorema
2.2 Daca siruri de
variabile aleatoare reale ![]() este convergent punctuial catre functia
este convergent punctuial catre functia ![]() atunci functia limita
atunci functia limita ![]() este tot mai
variabila aleatoare reala.
este tot mai
variabila aleatoare reala.
Demonstratie : Din
convergenta punctuala a sirului de variabile aleatoare
reale ![]() catre functia
catre functia
![]() rezulta marginirea punctuala a sirului de
variabile aleatoare reale si pentru orice
rezulta marginirea punctuala a sirului de
variabile aleatoare reale si pentru orice ![]() avem :
avem :
![]() .
.
Definitia
2.3. Vom spune ca un sir de variabile aleatoare reale ![]() este un sir Cauchy punctual daca pentru orice
este un sir Cauchy punctual daca pentru orice ![]() sirul
sirul ![]() este un sir de numere reale Cauchy sau fundamental.
este un sir de numere reale Cauchy sau fundamental.
Teorema 2.3. Sirul de variabile aleatoare reale este convergent punctual daca si numai daca este sir Cauchy punctual.
Demonstratie
. Din analiza reala se stie ca multimea numerelor reale R
este completa, adica un sir de numere reale este convergent
daca si numai daca este sir Cauchy.Prin urmare pentru orice
![]() sirul
sirul ![]() este un sir de numere reale convergent daca si
numai daca este un sir numeric Cauchy sau fundamental q.e.d.
este un sir de numere reale convergent daca si
numai daca este un sir numeric Cauchy sau fundamental q.e.d.
Definitia
2.4.Vom spune ca un sir de variabile aleatoare reale ![]() converge uniform catre o functie
converge uniform catre o functie ![]() , daca pentru orice
, daca pentru orice ![]() , exista
, exista ![]() astfel incat
astfel incat ![]() pentru orice
pentru orice ![]() .
.
Definitia
2.5.Vom spune ca un sir de variabile aleatoare reale ![]() este un sir Cauchy uniform (sau sir fundamental
uniform), daca pentru orice
este un sir Cauchy uniform (sau sir fundamental
uniform), daca pentru orice ![]() exista
exista ![]() astfel incat pentru orice
astfel incat pentru orice
![]() sa rezulte
sa rezulte ![]()
![]() pentru orice
pentru orice ![]() .
.
|
Teorema 2.4. Un sir de variabile aleatoare reale este convergent uniform daca si numai daca este un sir Cauchy uniform.
Demonstratie. Prima data sa presupunem ca
sirul de variabile aleatoare reale ![]() este convergent uniform , adica exista o
variabila aleatoare reala
este convergent uniform , adica exista o
variabila aleatoare reala ![]() pentru care daca
pentru care daca ![]() , atunci
, atunci ![]() pentru orice
pentru orice ![]() .Atunci daca
.Atunci daca ![]() , se obtine :
, se obtine :
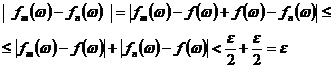
pentru
orice ![]() .Invers sa presupunem ca sirul de
variabilealeatoare reale
.Invers sa presupunem ca sirul de
variabilealeatoare reale ![]() este sir Cauchy uniform , deci pentru orice
este sir Cauchy uniform , deci pentru orice ![]() , exista
, exista ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() sa avem
sa avem ![]() pentru orice
pentru orice ![]() .
.
Pentru
un ![]() fixat rezulta ca sirul de numere reale
fixat rezulta ca sirul de numere reale ![]() este un sir numeric Cauchy, deci este convergent si
fie
este un sir numeric Cauchy, deci este convergent si
fie ![]() .Prin urmare sirul de variabile aleatoare
.Prin urmare sirul de variabile aleatoare ![]() este convergent punctual catre o variabila
aleatoare
este convergent punctual catre o variabila
aleatoare ![]() conform teoremei 11.2.2. In inegalitatea
conform teoremei 11.2.2. In inegalitatea ![]() trecem la limita dupa
trecem la limita dupa ![]() deci
deci ![]() daca
daca ![]() si pentru orice
si pentru orice ![]() .
.
3. Convergenta aproape sigura a sirurilor de variabile aleatoare reale
Fie ![]() o
o ![]() algebra de evenimente avand pe
algebra de evenimente avand pe ![]() evenimentul sigur, iar
evenimentul sigur, iar
![]() o probabilitate
o probabilitate ![]()
![]() aditiva.
aditiva.
Definitia
3.1. Vom spune ca o proprietate este valabila aproape sigur,
daca multimea evenimentelor elementare din ![]() care nu verifica aceasta proprietate formeaza
un eveniment din
care nu verifica aceasta proprietate formeaza
un eveniment din ![]() cu probabilitatea
zero.
cu probabilitatea
zero.
Exemplul Vom spune ca variabilele aleatoare ![]() verifica
relatia
verifica
relatia ![]() aproape sigur,
daca
aproape sigur,
daca ![]() , deoarece multimea
, deoarece multimea ![]() .Egalitatea anterioara se poate scrie si sub forma
echivalenta : doua variabile aleatoare reale verifica
relatia
.Egalitatea anterioara se poate scrie si sub forma
echivalenta : doua variabile aleatoare reale verifica
relatia ![]() aproape sigur, daca
aproape sigur, daca ![]() .Intr-adevar, evenimentul
.Intr-adevar, evenimentul ![]() este evenimentul contrar evenimentului
este evenimentul contrar evenimentului ![]() se aplica teorema 2.4.1.
se aplica teorema 2.4.1.
Definitia
3.2. Sirul de variabile aleatoare reale ![]() converge aproape sigur catre variabila aleatoare
converge aproape sigur catre variabila aleatoare ![]() , daca :
, daca :
![]() .
.
Pentru
convergenta aproape sigura vom folosi notatia ![]() , iar evenimentul
, iar evenimentul ![]() il vom nota cu
il vom nota cu ![]()
Conditia daca in definitia convergentiei aproape sigure este echivalenta cu relatia:
![]() .
.
Teorema
3.1. Fie ![]() si
si ![]() sunt doua siruri de variabile aleatoare reale, iar
sunt doua siruri de variabile aleatoare reale, iar ![]() doua variabile
aleatoare reale astfel incat
doua variabile
aleatoare reale astfel incat ![]() si
si ![]() .Atunci avem ca:
.Atunci avem ca:
![]() si
si ![]() .
.
Teorema
3.2. Daca pentru siruri de variabile aleatoare reale ![]() avem
avem ![]() si
si ![]() atunci
atunci ![]() .
.
Demonstratie Din unicitatea limitei rezulta
incluziunea ![]() . Trecand la evenimentele complementare obtinem :
. Trecand la evenimentele complementare obtinem :![]() .Aplicand proprietatile probabilitatii
avem :
.Aplicand proprietatile probabilitatii
avem : ![]() , deci
, deci ![]() , adica
, adica ![]() .
.
Definitia
2.3. Vom spune ca sirul de variabile aleatoare reale ![]() este sir Cauchy aproape sigur, daca :
este sir Cauchy aproape sigur, daca :
![]() .
.
Teorema 3.3. Sirul de variabile
aleatoare reale ![]() este sir Cauchy aproape sigur daca si numai
daca este sir convergent aproape sigur.
este sir Cauchy aproape sigur daca si numai
daca este sir convergent aproape sigur.
Mentionam
urmatorul rezultat, fara a da demonstratia, unde descriem
evenimentul ![]() :
:
Teorema 3.4. Avem
![]() .
.
Teorema
3.5. Daca sirul de
variabile aleatoare reale ![]() converge punctual catre variabila aleatoare reala
converge punctual catre variabila aleatoare reala ![]() , atunci
, atunci ![]() .
.
Demonstratie . Daca ![]() converge punctual catre
converge punctual catre ![]() atunci pentru orice
atunci pentru orice ![]() avem
avem ![]() , deci
, deci ![]() , adica
, adica ![]() .
.
4. Convergenta in probabilitate a sirurilor de variabile aleatoare reale
Fie ![]() o
o ![]() algebra de evenimente ,
algebra de evenimente , ![]() evenimentul sigur al
evenimentul sigur al ![]() algebrei, iar
algebrei, iar ![]() o probabilitate
o probabilitate ![]() aditiva.
aditiva.
Definitia
1.16.4.1. Sirul de variabile aleatoare reale ![]() converge in probabilitate catre variabila aleatoare
converge in probabilitate catre variabila aleatoare ![]() ,daca pentru orice
,daca pentru orice ![]() , fixat avem:
, fixat avem:
![]()
Pentru
convergenta in probabilitate vom folosi notatia ![]() .
.
Conditia data in definitia convergentei in probabilitate este echivalenta cu relatia :
![]()
Aceasta afirmatie rezulta imediat din faptul ca :
![]() .
.
Teorema
4.1.Urmatoarele afirmatii sunt echivalente pentru un sir de variabile aleatoare ![]() si variabila aleatoare
si variabila aleatoare ![]() :
:
i)
![]()
ii)
pentru orice ![]() si orice
si orice ![]() exista
exista ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() sa avem:
sa avem: ![]() , unde
, unde
![]() ,
,
iii)
pentru orice ![]() si orice
si orice ![]() exista
exista ![]() astfel incat pentru
orice
astfel incat pentru
orice ![]() sa avem :
sa avem : ![]() , unde :
, unde :
![]() .
.
Teorema
4.2. Daca ![]() si
si ![]() sunt doua siruri de variabile aleatoare reale, iar
sunt doua siruri de variabile aleatoare reale, iar ![]() sunt doua variabile aleatoare reale astfel incat
sunt doua variabile aleatoare reale astfel incat ![]() si
si ![]() , atunci avem :
, atunci avem : ![]() si
si ![]() .
.
Teorema.
4.3. Daca petru sirul de variabile aleatoare ![]() avem ca
avem ca ![]() si
si ![]() atunci
atunci ![]() .
.
Teorema
4.4. Daca pentru sirul de variabile aleatoare reale ![]() , avem
, avem ![]() , atunci
, atunci ![]() .
.
Teorema
4.5. Daca ![]() atunci exista un subsir
atunci exista un subsir ![]() al sirului de variabile aleatoare reale
al sirului de variabile aleatoare reale ![]() , astfel incat
, astfel incat ![]() .
.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2026 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Esee pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








