
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Calculul campului magnetic - proprietati magnetice ale substantei, caracterul vectorial al campului magnetic |
Calculul campului magnetic - proprietati magnetice ale substantei, caracterul vectorial al campului magnetic
CURS NR
1. Campul magnetic. Forte magnetice
2. Intensitatea campului magnetic
3. Caracterul vectorial al campului magnetic
4. Liniile campului magnetic
5. Fluxul campului magnetic
6. Actiunea campului magnetic asupra curentului electric
7. Campul magnetic al unei sarcini punctiforme
8. Campul magnetic al unui element de current. Legea Biot-Savart
9. Campul magnetic in central unei spire circulare
10. Campul magnetic al unui current rectiliniu infinit lung
11. Legea lui Ampère
12. Amperul unitate fundamental in SI
Legea lui Gauss pentru magnetism
Momentul magnetic atomic
Intensitatea de magnetizare
Campul magnetic H
Susceptibilitatea magnetica
Clasificarea substantelor dupa proprietatile lor magnetice
1. Campul magnetic. Forte magnetice
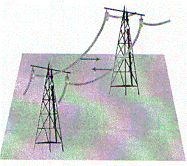 S-a constatat experimental ca intre doi conductori parcursi de curent electric se
manifesta forte de atractie
daca curentii au acelasi sens si de respingere daca conductorii sunt
parcursi de curenti electric in sens contrar. In conductori
exista atat sarcini pozitive (fixe) cat si sarcini electrice negative. In
ansamblu conductorul este neutru din
punct de vedere electric. Campul
electric generat de conductori neutri din punct de
vedere electric este nul. Deci orice
forta de natura electrica este si ea nula.
S-a constatat experimental ca intre doi conductori parcursi de curent electric se
manifesta forte de atractie
daca curentii au acelasi sens si de respingere daca conductorii sunt
parcursi de curenti electric in sens contrar. In conductori
exista atat sarcini pozitive (fixe) cat si sarcini electrice negative. In
ansamblu conductorul este neutru din
punct de vedere electric. Campul
electric generat de conductori neutri din punct de
vedere electric este nul. Deci orice
forta de natura electrica este si ea nula.
Istoric s-a mai constatat ca daca un magnet permanent(o busola) se gaseste in apropierea unui conductor parcurs de un curent electric atunci aceasta se reorienteaza.
Forta cu care actioneaza curentul electric asupra unui conductor parcurs si el de
curent electric sau asupra unui magnet se numeste Forta Magnetica.
Fig. 13.1 Conductorii parcursi de curent in acelasi sens se atrag.
Aceste fenomene nu mai pot fi explicate de mecanica Newtoniana pentru ca presupune aparitia unei forte chiar daca viteza electronilor este constanta si deci nu presupune o acceleratie.
2. Intensitatea campului magnetic
Definitie: Campul magnetic este o forma de existenta a materiei care se manifesta prin actiunea cu o forta de natura magnetica asupra sarcinilor electrice in miscare, deci si asupra curentilor eletrici.
Interactiunile magnetice se transmit de la un punct din spatiu la altul cu viteza finita, din aproape, prin intermediul campului magnetic. Viteza de propagare a interactiunii este egala cu viteza luminii.
![]()
(13.1)
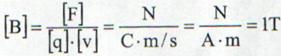 unde B este o masura a intensitatii campului
magnetic generat de sarcina q in miscare cu viteza v. Din motive istorice marimea B se numeste inductie
magnetica, si nu intensitate a campului magnetic.
unde B este o masura a intensitatii campului
magnetic generat de sarcina q in miscare cu viteza v. Din motive istorice marimea B se numeste inductie
magnetica, si nu intensitate a campului magnetic.
(13.2)
Definitie: Intr-un punct din spatiu campul magnetic are valoarea de un Tesla daca asupra sarcinii de 1C ce trece prin acel punct cu viteza de 1 m/s normala la camp, actioneaza o forta de 1N.
Interactiunea magnetica se propaga in doua etape:
In prima etapa sarcina q in miscare genereaza in jurul ei un camp magnetic care se propaga in spatiu.
In a doua etapa cand campul a ajuns la locul sarcinii in miscare acesta actioneaza asupra ei cu o forta magnetica.
3. Caracterul vectorial al campului magnetic
Experimental s-a constat ca exista directii particulare pentru care daca sacina q se misca in lungul uneia dintre ele atunci forta magnetica este nula. Exista si o alta directie perpendiculara pe prima pentru care forta magnetica este maxima
![]() (13.3)
(13.3)
care este forta Lorentz.
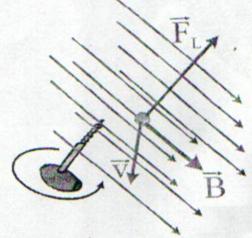
![]()
![]() Orientarea fortei magnetice care
actioneaza asupra sarcinii in
miscare cu viteza
Orientarea fortei magnetice care
actioneaza asupra sarcinii in
miscare cu viteza ![]() ,
in campul magnetic este in
directia in care inainteaza un burghiu drept cand este rotit in
sensul in care se poate suprapune vectorul
,
in campul magnetic este in
directia in care inainteaza un burghiu drept cand este rotit in
sensul in care se poate suprapune vectorul ![]() peste vectorul
peste vectorul ![]() pe drumul cel mai scurt.
pe drumul cel mai scurt.
Fig. 13.2 Forta Lorentz. Regula burghiului
Regula maini stangi pentru stabilirea orientarii fortei Lorentz: Daca degetele mainii stangi deschise sunt orientate in sensul vitezei de deplasare a unei sarcini pozitive astfel incat campul magnetic sa intre in palma atunci degetul mare indica directia fortei Lorentz.
4. Liniile campului magnetic
Fiecarui punct din campul magnetic i se poate atasa un vector, ![]() Linia de camp care are ca tangenta in
orice punct un vector camp magnetic se numeste linie de camp magentic.
Linia de camp care are ca tangenta in
orice punct un vector camp magnetic se numeste linie de camp magentic.
Proprietatiile liniilor de camp magnetic:
Printr-un punct din spatiu trece o singura linie de camp magnetic.
Liniile campului magnetic nu se pot intersecta.
Liniile campului magnetic sunt curbe inchise.
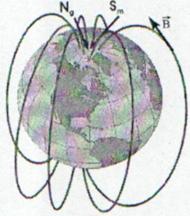
● Liniile campului magnetic sunt curbe orientate. Orientarea liniei de camp intr-un punct din spatiu este data de directia in care se orienteza polul nord al unui ac de busola care se plaseaza in acel punct. Daca campul magnetic este produs de un magnet atunci liniile cimpului magnetic ies din polul nord al magnetului si intra in polul sud al magnetului.
Fig. 13.3 Campul magnetic terestru
5. Fluxul campului magnetic
Definitie: Se numeste flux al
campului magnetic printr-o suprafata oarecare ![]() si se noteaza prin Φm numarul liniilor de camp
magnetic care strabat unitatea de suprafata
si se noteaza prin Φm numarul liniilor de camp
magnetic care strabat unitatea de suprafata ![]() normala la linii.
normala la linii.
![]() (13.4)
(13.4)
![]() pentru un camp
magnetic omogen. Daca in schimb campul magnetic
este neomogen atunci se poate considera o portiune infinitezimala de
suprafata pentru care campul magnetic variaza atat de putin
incat campul magnetic poate fi considerat constant:
pentru un camp
magnetic omogen. Daca in schimb campul magnetic
este neomogen atunci se poate considera o portiune infinitezimala de
suprafata pentru care campul magnetic variaza atat de putin
incat campul magnetic poate fi considerat constant:
 (13.5)
(13.5)
atunci fluxul magnetic printr-o suprafata S
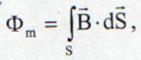 este:
este:
(13.6)
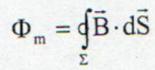 iar daca suprafata este inchisa atunci:
iar daca suprafata este inchisa atunci:
(13.7)
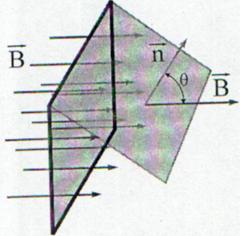
Fig. 13.4 Fluxul campului magnetic printr-o
suprafata orientata.
Actiunea campului magnetic asupra curentului electric
Forta magnetica asupra unui element curent
Definitie: Prin element de curent intelegem o portiune dintr-un conductor subtire, cu lungime dl atat de mica incat sarcina totala dQ a purtatorilor de curent din interiorul lui poate fi considerata punctiforma.
Daca elementul de curent este parcurs de un curent de intensitate I atunci elmentul de circuit este caracterizat de produsul I.dl. Daca asa cum s-a presupus sarcina dQ este punctiforma atunci se poate aplica legea lui Lorentz pentru a calcula elementul de forta, dF
![]() (13.8)
(13.8)
daca aria sectiunii elementului de curent este a sarcina unui purtator este q iar concentratia purtatorilor este n atunci se poate calcula elementul de sarcina ca fiind:
![]() (13.9)
(13.9)
de unde elementul de forta devine:
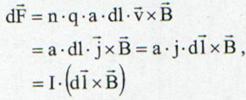
|
(13.10)
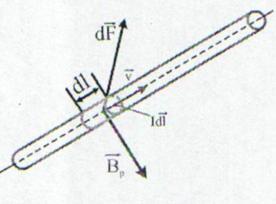
Fig. 13.5 Orientarea fortei magnetice
unde s-a tranferat caracterul vectorial de la viteza la elementul de lungime.
![]() (13.11)
(13.11)
Forta magnetica asupra unui curent liniar infinit
Presupunem un conductor liniar de lungime L prin care trece un curent electric de intensitate I si care se gaseste intr-un camp magnetic, B. Forta care actioneaza asupra acestui conductor este data de:
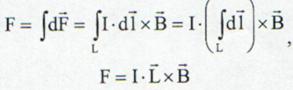
(13.12)
care este legea lui Laplace.
Forta magnetica asupra unui curent inchis
Curentul electric circula intr-un circuit numai daca este inchis prin intermediul sursei de tensiune electromotoare. Elementele de circuit trebuie sa faca parte dintr-un circuit. Deoarece circuitul inchis nu poate fi rectiliniu elementele de curent nu sunt paralele. Mai mult daca aplicam regula paralelogramului pentru compunerea vectorilor atunci obtinem:
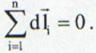 (13.13)
(13.13)
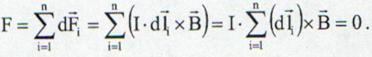 Forta
totala magnetica este data de suma fortelor magnetice
elementare:
Forta
totala magnetica este data de suma fortelor magnetice
elementare:
(13.13)
Forta magnetica ce actioneaza asupra unui circuit inchis aflat in camp magnetic omogen este nula.
7. Sursele campului magnetic
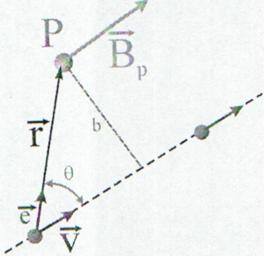
Campul magnetic al unei sarcini punctiforme
![]()
![]() Se pune intrebarea:
Care este orientarea vectorului
Se pune intrebarea:
Care este orientarea vectorului ![]() in campul sarcinii punctiforme
? Raspunsul este simplu: Fie un punct P aflat la momentul t in pozitia data
de vectorul de pozitie
in campul sarcinii punctiforme
? Raspunsul este simplu: Fie un punct P aflat la momentul t in pozitia data
de vectorul de pozitie ![]() de sarcina, q, care in miscarea cu viteza v genereaza un camp magnetic .Daca este versorul vectorului de pozitie
atunci expresia campului magnetic al sarcinii
punctifor-
de sarcina, q, care in miscarea cu viteza v genereaza un camp magnetic .Daca este versorul vectorului de pozitie
atunci expresia campului magnetic al sarcinii
punctifor-
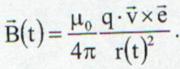 me q in punctul P poate fi scrisa sub forma:
me q in punctul P poate fi scrisa sub forma:
(13.14)
Vectorul camp magnetic ![]() generat
generat
de o sarcina
punctiforma, intr-un punct oarecare P
este perpendicular pe planul format de vectorii ![]() si este
orientat in sensul vectorului
si este
orientat in sensul vectorului ![]()
Fig. 13.6 Campul magnetic al unei sarcini punctiforme.
8. Legea Biot-Savart
Campul magnetic al unui element de curent
In locul unei sarcini punctiforme consideram un element de current
liniar ![]() Sarcina din interiorul
lui este data de ecuatia (13.9). Sarcina dQ poate fi considerata
punctiforma. Atunci prin aplicarea ecuatiei (13.14) obtinem
elemental de camp magnetic in punctul P
ca fiind:
Sarcina din interiorul
lui este data de ecuatia (13.9). Sarcina dQ poate fi considerata
punctiforma. Atunci prin aplicarea ecuatiei (13.14) obtinem
elemental de camp magnetic in punctul P
ca fiind:
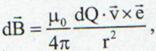
(13.15)
unde v este viteza in current a purtatorilor de sarcina. Astfel inlocuind elemental de sarcina electrica obtinem:
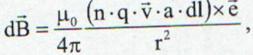
(13.16)
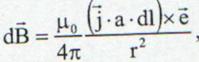 iar daca se
introduce
iar daca se
introduce
(13.17)
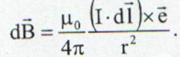 de unde se poate
obtine legea lui Biot-Savart.
de unde se poate
obtine legea lui Biot-Savart.
(13.17)
Legea lui Biot-Savart ne da
valoarea si orientarea campului magnetic generat de elementul de curent ![]() intr-un
punct P situat la distanta r de elementul de curent.
intr-un
punct P situat la distanta r de elementul de curent.
Vectorul camp magnetic elementar ![]() generat de
elementul de curent
generat de
elementul de curent ![]()
![]() intr-un punct situat la
distanta r de acesta, este orientat normal la planul format de
vectorii al
vectorului de pozitie al punctului P, in sensul in care inainteaza un
burghiu drept cand este rotit in sensul in care putem suprapune vectorul
intr-un punct situat la
distanta r de acesta, este orientat normal la planul format de
vectorii al
vectorului de pozitie al punctului P, in sensul in care inainteaza un
burghiu drept cand este rotit in sensul in care putem suprapune vectorul ![]() peste vectorul
peste vectorul
![]() pe drumul cel
mai scurt.
pe drumul cel
mai scurt.
Campul magnetic al unui element de curent
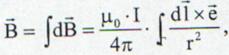 Un conductor oarecare de lungime finita parcurs de
un curent electric I poate fi divizat in mai multe elemente de curent. Campul
magnetic intr-un punct P este dat de suma vectoriala a contributiei
fiecarui astfel element curent. La limita se obtine integrala:
Un conductor oarecare de lungime finita parcurs de
un curent electric I poate fi divizat in mai multe elemente de curent. Campul
magnetic intr-un punct P este dat de suma vectoriala a contributiei
fiecarui astfel element curent. La limita se obtine integrala:
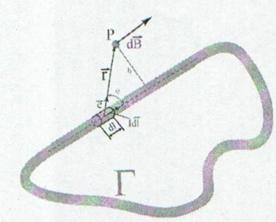 (13.18)
(13.18)
care reprezinta forma integrala a legii
Biot-Savart.
Orientarea vectorului ![]()
Depinde de forma concreta a conduc-
torului si coincide cu orientarea rezul-
tantei tuturor campurilor elementare
![]() generate de
elementele de curent
generate de
elementele de curent
din care este construit conductorul.
Fig. 13.7 Campul magnetic produs de un
lement de curent.
9. Campul magnetic in centrul unei spire circulare
Sa consideram o spira circulara cu raza r, parcursa de un curent cu intensitatea I. Ne intereseaza campul magnetic in centrul ei. Toate campurile magnetice provenite de la elementele de curent au aceeasi orientare, si anume in lungul axei spirei, avand in plus si acelasi sens, cel dat de inaintarea unui burghiu drept. Insumarea vectoriala a campurilor magnetice poate fi inlocuita de insumarea scalara a modulelor lor.
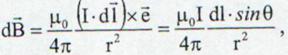 (13.19)
(13.19)
dar indiferent de elementul de volum ales unghiul dintre versorul razei
vectoare ![]() si
elementul de lungime
si
elementul de lungime ![]() este θ
= 90s. Obtinem atunci:
este θ
= 90s. Obtinem atunci:
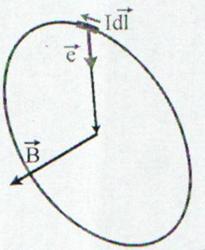
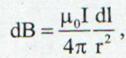
(13.20)
de unde prin integrare
![]()
se obtine campul magnetic produs de o spira
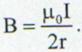 circulara
in centrul ei:
circulara
in centrul ei:
(13.22)
Fig. 13.8 Campul magnetic in centrul unei spire
Definitie: Campul magnetic in centrul unei spire circulare parcursa de curent electric este direct proportional cu intensitatea curentului prin spira si invers proportional cu raza spirei.
10. Campul magnetic al unui curent rectiliniu infinit lung
![]()
![]() Consideram un conductor rectiliniu, infinit lung, prin care trece
un curent cu intensitatea I. Ne intereseaza intensitatea campului magnetic
intr-un punct P situat la distanta b de conductor. Impartim
conductorul in elemente de curent. Campul magnetic al acestor elemente de
curent este perpendicular atat pe versorul
Consideram un conductor rectiliniu, infinit lung, prin care trece
un curent cu intensitatea I. Ne intereseaza intensitatea campului magnetic
intr-un punct P situat la distanta b de conductor. Impartim
conductorul in elemente de curent. Campul magnetic al acestor elemente de
curent este perpendicular atat pe versorul ![]() si
elementul de curent
si
elementul de curent ![]() In plus au
aceeasi orientare pentru toate elementele care apartin conductorului
rectiliniu.
In plus au
aceeasi orientare pentru toate elementele care apartin conductorului
rectiliniu.
(13.23)
se observa ca:
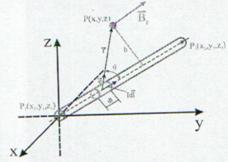
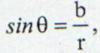
(13.24)
si:
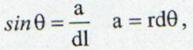 (13.25)
(13.25)
de unde se obtine:
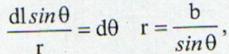 (13.26)
(13.26)
Fig. 13.9 Campul magnetic al unui curent
rectiliniu.
care inlocuite in ecuatia (13.23) se obtine:
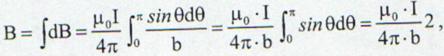
(13.27)
de unde:
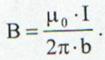 (13.28)
(13.28)
Definitie:Campul magnetic al curentului liniar, infinit lung, intr-un punct din spatiu este direct proportional cu intensitatea curentului electric si invers proportional cu distanta de la axa conductorului la punctul considerat.
Observatie: Liniile campului magnetic al curentului rectiliniu, infinit de lung sunt cercuri concentrice in plane perpendiculare pe conductor si centrate pe axa conductorului.
11. Legea lui Ampere
Ne intereseaza care este circulatia campului stationar pe un contur inchis .Consideram doua cazuri i)cand controlul nu incercuieste un curent I si ii) cand conturul incercuieste un curent I .
I.Conturul nu incercuieste un curent I
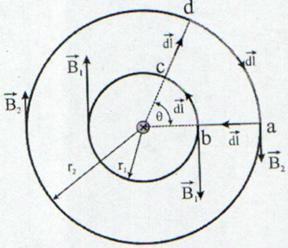
Alegem un contur de integrare
particular C abcda, in campul mag-
netic al curentului I. Descompunem
conturul (si integrala) in 4 portiuni
doua segmente radiale si doua arcuri
![]() de
cerc. Pe segmentele radiale (ab) si
de
cerc. Pe segmentele radiale (ab) si
(cd) elementul de contur
in timp ce pe arcele de cerc (bc) si (da
cele
doua sunt ![]() antiparalele pe
antiparalele pe
(bc) si paralele pe (da). Circulatia vec-
![]() torului in lungul conturului C este:
torului in lungul conturului C este:
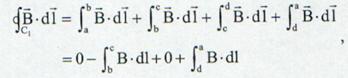 Fig. 13.10 Legea lui Ampere pentru un contur
care nu incercuieste curentul.
Fig. 13.10 Legea lui Ampere pentru un contur
care nu incercuieste curentul.
(13.29)
care prin utilizarea relatiei ( 13.28) devine:
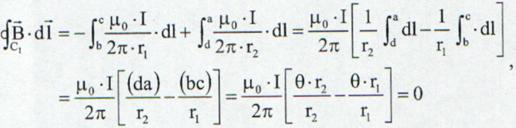
(13.30)
de unde se obtine
circulatia vectorului ![]() in lungul conturului C care este in
afara curentului I:
in lungul conturului C care este in
afara curentului I:
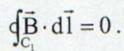
(13.31)
II. Conturul incercuieste un curent I
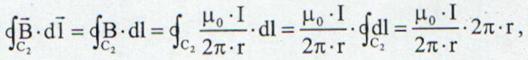 Cel mai
simplu contur care incercuieste curentul I este cercul C
Cel mai
simplu contur care incercuieste curentul I este cercul C
(13.32)
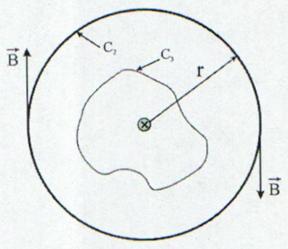
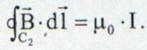 de unde se obtine circulatia vectorului
de unde se obtine circulatia vectorului ![]() in lungul conturului C care
incercuieste curentul I ca fiind:
in lungul conturului C care
incercuieste curentul I ca fiind:
(13.33)
Se poate arata ca ecuatia (13.33)
Este adevarata pentru orice contur care incercuieste curentul I.
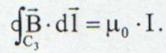
(13.34)
Mai mult este adevarata si pentru
un contur care nu se gaseste intr-un
plan perpendicular pe curentul I.
Fig. 13.11 Legea lui Ampere pentru un contur care incercuieste curentul.
Intr-adevar, daca
consideram un curent I inconjurat de un contur inchis arbitrar Г. Prin orice punct, P al
conturului putem trasa o linie de camp magnetic si vectorul ![]() tangent la ea.
Daca se noteaza cu α unghiul dintre campul
tangent la ea.
Daca se noteaza cu α unghiul dintre campul ![]() si
elementul de contur
si
elementul de contur ![]() Atunci
proiectia lui
Atunci
proiectia lui ![]() pe campul
pe campul ![]()
este ![]()
![]()
(13.35)
de unde circulatia vectorului ![]() in lungul
conturului Г care incercuieste cu-
in lungul
conturului Г care incercuieste cu-
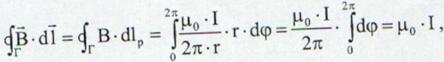 rentului I este data de relatia:
rentului I este data de relatia:
(13.36)
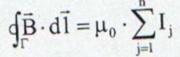 care este aceeasi cu ecuatia (13.34). Daca
conturul de integrare incercuieste mai multi curenti atunci se
considera suma algebrica a celor care se gasesc in interiorul
conturului inchis Г:
care este aceeasi cu ecuatia (13.34). Daca
conturul de integrare incercuieste mai multi curenti atunci se
considera suma algebrica a celor care se gasesc in interiorul
conturului inchis Г:
(13.37)
Ecuatia (13.37) este legea lui Ampère. Enuntul legii lui Ampère: Circulatia
campului magnetic ![]() pe un contur inchis este egala cu
produsul dintre permeabilitatea magnetica a vidului, μ si suma algebrica a curentilor incercuiti de conturul
de integrare Г.
pe un contur inchis este egala cu
produsul dintre permeabilitatea magnetica a vidului, μ si suma algebrica a curentilor incercuiti de conturul
de integrare Г.
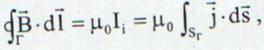 Daca conturul de integrare se gaseste in
interiorul unui conductor masiv atunci putem scrie:
Daca conturul de integrare se gaseste in
interiorul unui conductor masiv atunci putem scrie:
(13.38)
care este legea lui Ampère sub forma integrala. Suprafata S pe care se calculeaza integrala din densitatea de curent poate avea orice forma atata timp cat se sprijina pe conturul Г.
![]() Enuntul legii lui Ampère sub forma integrala: Circulatia campului
magnetic pe un contur inchis Г
este egala cu produsul dintre permeabilitatea magnetica a vidului,
μ si integrala densitatii de
curent pe o suprafata de se sprijina cu marginea pe conturul de
integrare Г.
Enuntul legii lui Ampère sub forma integrala: Circulatia campului
magnetic pe un contur inchis Г
este egala cu produsul dintre permeabilitatea magnetica a vidului,
μ si integrala densitatii de
curent pe o suprafata de se sprijina cu marginea pe conturul de
integrare Г.
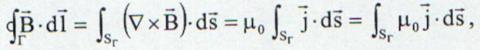 Legea lui Ampère este o alta
forma de exprimare a legii lui Biot-Savart. In plus daca folosim
teorema lui Stockes putem obtine legea lui Ampère sub forma
diferentiala:
Legea lui Ampère este o alta
forma de exprimare a legii lui Biot-Savart. In plus daca folosim
teorema lui Stockes putem obtine legea lui Ampère sub forma
diferentiala:
(13.39)
![]() de unde:
de unde:
(13.40)
12. Amperul unitate fundamentala in SI
Pentru definirea Amperului consideram doi conductori rectilinii paraleli, infiniti parcursi de curent electric situati in vid la distanta d = 1m unul de celalalt prin care circula curentii electrici I si respectiv I Campul magnetic generat de curentul I in punctul in care se gaseste curentul I este:
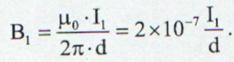 (13.41)
(13.41)
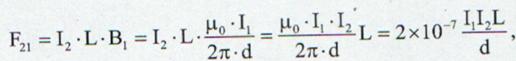 Conform
Legii lui Laplace forta care actioneaza asupra curentului I este atunci:
Conform
Legii lui Laplace forta care actioneaza asupra curentului I este atunci:
(13.42)
![]()
din aceleasi motive forta care actioneaza asupra curentului I este
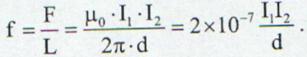 Forta de interactie dintre cei doi conductori
ce revine unitatii de lungime este:
Forta de interactie dintre cei doi conductori
ce revine unitatii de lungime este:
(13.43)
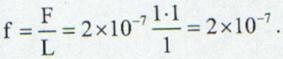 Daca intensitatea curentului electric
este aceeasi in cei doi conductori si
Daca intensitatea curentului electric
este aceeasi in cei doi conductori si ![]() atunci forta
unitatii de lungime devine:
atunci forta
unitatii de lungime devine:
(13.44)
Definitie: Amperul este intensitatea curentului electric continuu
care este mentinut in doi conductori rectilinii, paraleli, de lungime
infinita si sectiune neglijabila, situati in vid la
distanta de 1m unul de altul, si care interactioneaza intre
ei cu o forta de ![]()
Legea lui Gauss pentru magnetism
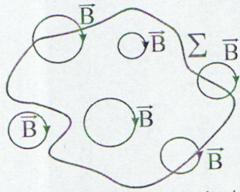
Campul magnetic se caracterizeaza prin linii de camp inchise. Acest lucru inseamna ca orice linie care intra intr-o suprafata inchisa trebuie sa iasa din ea. Acest lucru ne spune ca fluxul magnetic total printr-o suprafata inchisa este egal cu zero.
![]()
(13.45)
care este legea lui Gauss, forma integrala, pentru campul magnetic. Ea este
 satisfacuta
si de campurile magnetice varia-
satisfacuta
si de campurile magnetice varia-
bile in timp.
Enunt: Fluxul campului magnetic
printr-o suprafata inchisa este egal cu zero.
O consecinta a legii lui Gauss pentru
campurile magnetice este acea ca in natura
nu exista sarcini magnetice individuale
(monopoli magnetici).
Fig. 13.12 Legea lui Gauss pentru campul magnetic.
Daca ne folosim de teorema divergentei ecuatia (13.45) devine:
![]()
(13.46)
![]() de unde rezulta legea lui Gauss pentru campul magnetic forma
diferentiala ca fiind:
de unde rezulta legea lui Gauss pentru campul magnetic forma
diferentiala ca fiind:
13 .14. Momentul magnetic atomic
![]() Dorim
sa examinam acum influenta pe care o au mediile materiale asupra
campului magnetic. Experienta arata ca toate substantele se
magnetizeaza cind sunt introduse in camp magnetic. Efectul
magnetizarii substantelor este modificarea valorii initiale a
campului magnetic, atat in interiorul substantei cat si in
spatiul din vecinitatea ei. Daca notam cu
Dorim
sa examinam acum influenta pe care o au mediile materiale asupra
campului magnetic. Experienta arata ca toate substantele se
magnetizeaza cind sunt introduse in camp magnetic. Efectul
magnetizarii substantelor este modificarea valorii initiale a
campului magnetic, atat in interiorul substantei cat si in
spatiul din vecinitatea ei. Daca notam cu ![]() campul magnetic in vid (aer) si
cu campul magnetic in prezenta
substantei atunci in orice punct din substanta putem scrie
relatia:
campul magnetic in vid (aer) si
cu campul magnetic in prezenta
substantei atunci in orice punct din substanta putem scrie
relatia:
![]() (13.48)
(13.48)
unde ![]() este campul magnetic generat de
substanta magnetizata.
este campul magnetic generat de
substanta magnetizata.
Am vazut mai inainte ca un curent electric produce in jurul lui un camp magnetic. Dar curentul electric nu este altceva decat sarcina electrica in miscare. Deci putem spune ca sursele campului magnetic sunt de fapt sarcinile electrice in miscare. Doar ca in prezenta substantei trebuie sa facem distinctie intre:
. Miscarea sarcinilor electrice libere, in vid sau in conductori,
. Miscarea electronilor legati in atomi sau molecule.
Definitie: Curentii electrici datorati miscarii ordonate a sarcinilor electrice libere se numesc curenti liberi.
Definitie: Curentii electrici datorati miscarii ordonate a sarcinilor electrice legate in atomi sau molecule se numesc curenti legati sau curenti de magnetizare.
Intensitatea curentului atomic orbital
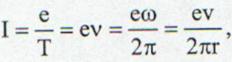 Consideram o orbita atomica circulara de raza r, pe care se misca un
electron cu sarcina e.Intr-o
perioada, T prin orice sectiune transversala a orbitei
electronul trece o singura data. De aici intensitatea curentului
electric este egala cu:
Consideram o orbita atomica circulara de raza r, pe care se misca un
electron cu sarcina e.Intr-o
perioada, T prin orice sectiune transversala a orbitei
electronul trece o singura data. De aici intensitatea curentului
electric este egala cu:
(13.49)
 unde v este frecventa de
rotatie a elec-
unde v este frecventa de
rotatie a elec-
tronului ω- viteza liniara a miscarii de
rotatie.
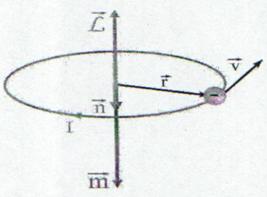
Fig. 13.13 Miscarea electronului pe orbita in
jurul nucleului conduce la aparitia unui mo-
ment cinetic si la aparitia unui moment mag-
netic.
Momentul magnetic al curentului atomic orbital
Daca consideram aria orbitei circulare ca fiind S = πr² atunci putem definii momentul magnetic:
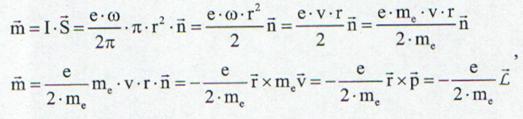
de unde momentul magnetic al curentului atomic orbital este:
![]() (13.51)
(13.51)
![]()
![]() Fiecare orbita electronica
din atomi se caracterizeaza printr-un moment magnetic orientat in sens opus momentului
cinetic al electronului.
Relatie in care s-a definit raportul (factorul) giromagnetic ca fiind:
Fiecare orbita electronica
din atomi se caracterizeaza printr-un moment magnetic orientat in sens opus momentului
cinetic al electronului.
Relatie in care s-a definit raportul (factorul) giromagnetic ca fiind:
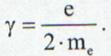
(13.52)
Definitie:Factorul giromagnetic,y este
numeric egal cu raportul modulelor momentului magnetic orbital ![]() si momentul cinetic orbital
si momentul cinetic orbital ![]()
Momentul magnetic atomic
Pe
langa momentul magnetic orbital electronul se caracterizeaza printr-un
moment
magnetic de spin ![]() Momentul magnetic total al unui
electron atomic este egal cu suma vectoriala a momentelor sale magnetice:
orbital si de spin.
Momentul magnetic total al unui
electron atomic este egal cu suma vectoriala a momentelor sale magnetice:
orbital si de spin.
Definitie:Momentul magnetic atomic este egal cu suma vectoriala a momentelor magnetice orbital si de spin ale electronilor si a momentului magnetic al nucleului.
Tinand cont de faptul ca raportul dintre masa protonului si cel al electronului mn/me= 1840 de cele mai multe ori se poate neglija.
15. Intensitatea de magnetizare
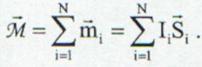 Ne putem imagina substantele ca
fiind compuse dintr-o multime de curenti amperici (curenti
lageti de atomi), caracterizat fiecare prin momentul sau
magnetic.Daca intr-o portiune de material cu volumul V exista N curenti atomici atunci momentul magnetic total este:
Ne putem imagina substantele ca
fiind compuse dintr-o multime de curenti amperici (curenti
lageti de atomi), caracterizat fiecare prin momentul sau
magnetic.Daca intr-o portiune de material cu volumul V exista N curenti atomici atunci momentul magnetic total este:
(13.53)
Momentul magnetic al unitatii de volum este o marime fizica mult mi potrivita pentru a caracteriza magnetizarea unui material:
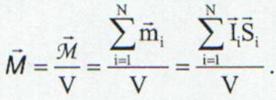
Definitie:Momentul magnetic al unitatii de volum se numeste intensitate de magnetizare sau magnetizare.
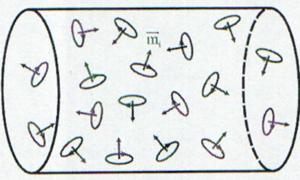 In general daca o
portiune de
In general daca o
portiune de
material nu se gaseste in camp
magnetic, orbitele curentilor am-
perici in interiorul ei (si momente-
le magnetice asociate) sunt orien-
tate complet haotic iar magneti-
zarea totala este egala cu zero.
Trebuie mentionat ca exista si
Fig. 13.14 Curentii amperici si momentele magnetice
asociate, datorate miscarii electronilor pe orbite sunt orientate aleator.
substante care fac exceptie de la aceasta regula.
16. Campul magnetic H
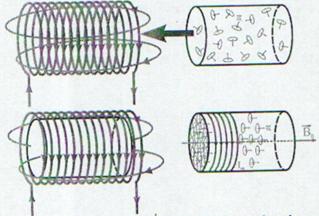
Daca consideram un solenoid avand in interiorul sau un cilindru care la trecerea curentului electric se magnetizeaza. Legea lui Ampere se scrie ca:
![]() (13.55)
(13.55)
unde NI
este curentul liber iar Imeste
curentul de magnetizare, iar ![]() este evident campul magnetic generat de
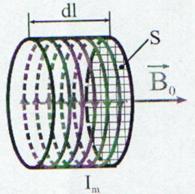
curentii liberi si de curentii de magnetizare. Consideram o
felie a cilindrului magnetizat de lungime dl
taiata normal la axa cilindrului. Daca intensitatea
curentului de magnetizare
este evident campul magnetic generat de
curentii liberi si de curentii de magnetizare. Consideram o
felie a cilindrului magnetizat de lungime dl
taiata normal la axa cilindrului. Daca intensitatea
curentului de magnetizare
![]()
 ce curge pe suprafata acestei
ce curge pe suprafata acestei
felii este atunci momen-
tul magnetic asociat este:
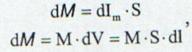
(13.56)
de unde intensitatea elemen-
tara a curentului de magnetizare
este:
![]()
Fig. 13.15 Aparitia curentului de magnetizare la
suprafata substantelor introduce in camp magnetic.
 de
unde intensitatea curentului de magnetizare
de
unde intensitatea curentului de magnetizare
este:
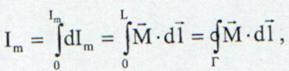
unde pe
restul (exceptand portiunea L) portiunii din curba,magnetizarea
M=0. Curentul de magnetizare genereaza campul magnetic ![]()
Fig. 13.16 Aparitia curentului de in interiorul cilindrului si in vecinatatea lui.
magnetizare la suprafata substantelor introduce in camp magnetic.
Astfel legea lui Ampere data de ecuatia (13.55) se rescrie ca fiind:
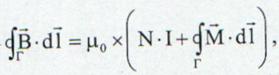
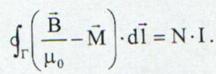 sau
sau
(13.60)
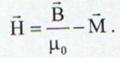 Putem
nota intensitatea campului magnetic ca fiind:
Putem
nota intensitatea campului magnetic ca fiind:
(13.61)
![]() sau:
sau:
(13.62)
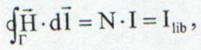 iar legea lui Ampere devine:
iar legea lui Ampere devine:
(13.63)
unde ![]() este intensitatea curentului liber
total, inconjurat de conturul Г.
este intensitatea curentului liber
total, inconjurat de conturul Г.
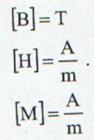
17. Susceptibilitatea magnetica
![]()
La
o temperatura data valoarea unui material, depinde de valoarea campului
magnetizator, ![]()
![]()
(13.65)
unde constanta de proportionalitate, mse numeste susceptibilitate magnetica si depinde de natura substantei (si de temperatura in anumite cazuri).
![]()
![]() unde:
unde:
(13.67)
se numeste permeabilitate magnetica relativa a materialului.De aici se poate defini permeabilitatea absoluta a materialului ca fiind:
![]()
(13.68)
18. Clasificarea substantelor dupa proprietatile lor magnetice
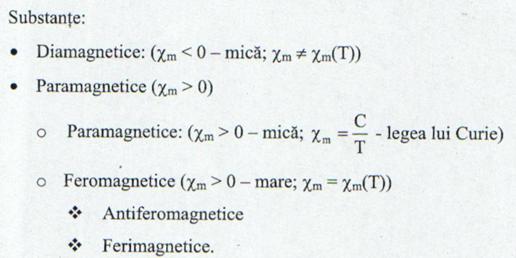
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Referate pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








