
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Matematica
|
|
Qdidactic » didactica & scoala » matematica Algoritmul de codare Huffman |
Algoritmul de codare Huffman
1. Obiectivul lucrarii
Se studiaza algoritmii Huffman (binar si ternar) de codare compacta a datelor pentru canale fara perturbatii si se analizeaza caracteristicile si performantele codurilor obtinute.
2. Introducere teoretica
Algoritmul de codare Huffman este optimal in sensul ca nici un alt algoritm de codare D-ara a unei surse discrete Q-are nu conduce la un cod de lungime medie a cuvintelor de cod mai mica, in cazul codarii simbolurilor individuale.
Conditia necesara si suficienta de existenta a unui cod fara prefix, de alfabet de dimensiune D si cu lungimile cuvintelor de cod l1, l2,.lQ, unde Q este dimensiunea alfabetului sursei primare, si totodata dimensiunea vocabularului codului, este (inegalitatea Kraft-McMillan):
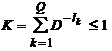
Se considera, pentru inceput, cazul codurilor binare, D = 2. Pentru un cod de alfabet binar, inegalitatea Kraft-McMillan devine:
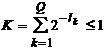
Pentru orice sursa discreta Q-ara, un cod fara prefix optimal in raport cu minimizarea lungimii medii a cuvintelor de cod are urmatoarele proprietati:
(i) Daca p(uj) > p(uk), atunci ![]()
(ii) Ultimelor doua simboluri de cea mai mica probabilitate din alfabetul sursei le corespund cuvinte de cod de aceeasi lungime si care difera numai prin ultimul simbol.
Aceste proprietati sugereaza urmatoarea procedura de constructie: se combina cele doua simboluri de cea mai mica probabilitate intr-un nou simbol artificial de probabilitate egala cu suma probabilitatilor celor doua simboluri originale. Se obtine o noua sursa cu Q-1 simboluri. Trebuie, acum, sa se construiasca un cod optimal pentru aceasta noua sursa. Pentru obtinerea cuvintelor de cod corespunzatoare celor doua simboluri de cea mai mica probabilitate ale sursei originale se adauga un "0" si, respectiv, un "1" cuvantului alocat simbolului artificial creat. Pentru a gasi codul optimal, se repeta procedura. Se combina cele doua simboluri de cea mai mica probabilitate a sursei artificiale si se obtine o a doua sursa artificiala pentru care se cauta un cod nou optimal s.a.m.d.
Algoritmul Huffman cuprinde, atunci, urmatorii pasi:
Pas 1: Se ordoneaza simbolurile sursei primare Q-are in sens descrescator al probabilitatilor,
![]()
si se noteaza sursa primara prin R0, adica sursa restransa de ordinul zero.
Pas 2: Se grupeaza ultimele doua simboluri de cele mai mici probabilitati, uk-1 si uk, intr-un simbol artificial r1 avand probabilitatea
![]()
Pas 3: Se asigneaza litera 1 simbolului uk-1 si 0, simbolului uk (sau invers) din grupul r1.
Pas 4: Se repeta pasii 1 si 2 pentru noua sursa artificiala obtinuta, numita si sursa restransa de ordinul intai, R1, si pentru sirul de surse restranse de ordinul al doilea, R2, al treilea, R3, , Rn, pana cand se obtine sursa restransa de ordinul n = Q-2, care furnizeaza doar doua simboluri artificiale.
Pas 5: Cuvantul de cod complet, corespunzator unui simbol al sursei primare, este constituit din secventa literelor codului obtinuta prin parcurgerea surselor restranse in sensul opus restrangerii, pana la gasirea simbolului original; aceasta echivaleaza cu parcurgerea unui arbore de la un nod final la radacina.
|
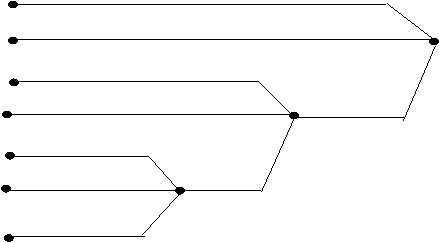
Daca probabilitatile celor doua simboluri reunite in simbolul artificial rj selectat la fiecare restrangere sunt egale, se poate obtine un cod absolut optimal (cu eficienta unitara). In caz contrar se obtine un cod optimal cu atat mai apropiat de unul absolut optimal cu cat diferenta dintre probabilitatile celor doua elemente ale lui rj este mai mica. Un exemplu de codare binara Huffman este prezentat sub forma unui graf arbore, desenat de la nodurile finale spre radacina, in figura 1. Pentru codul C1 rezulta urmatoarele valori caracteristice:
H(U) = 2,3 bit / simbol
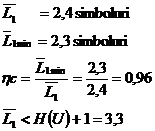
u1
1 0,55 1
u2
0 1,00
u3
1
u4 0,45 0
1
u5 0,10 0,25 0
1 0,15 0
u6
0
R0 R1 R2 R3 R4
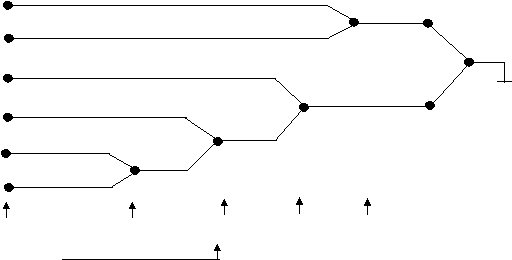 Surse
Surse
restranse
C 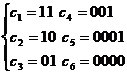
Fig. 1. Graful arbore pentru algoritmul Huffman binar
In cazul utilizarii unui cod cu alfabet D-ar, in pasul 2 se grupeaza ultimele D simboluri de cele mai mici probabilitati, iar in pasul 3 se asigneaza D litere (0, 1, , D-1) celor D litere din simbolul artificial r1; dupa prima restrangere se obtine o sursa restransa (artificiala) cu (Q-D)+1 simboluri, iar dupa n restrangeri, o sursa cu (Q-nD)+n simboluri. Pentru ca operatia de codare sa fie posibila, ultima sursa restransa trebuie sa furnizeze D simboluri, deci D = (Q-nD)+n, de unde rezulta un numarul de restrangeri
![]()
Un exemplu de codare Huffman ternara (D = 3) este prezentat in fig. 2.
Pentru codul din exemplul anterior rezulta parametrii
H(U) = 2,3 bit / simbol
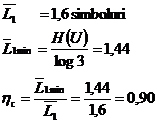
u1 0
u2 1 1,00
![]()
![]() u3 2
u3 2
0
u4 0,10 1 0,45
u5 0,10 2
0
u6 1 0,15
u7 0,01 2
R0 R1 R2
![]() restrangeri
restrangeri
C 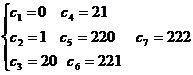
Fig. 2. Graful arbore pentru algoritmul Huffman ternar
Daca se doreste cresterea eficientei, se poate trece la codare pe grupe de simboluri sau pe blocuri de lungime > 1 (de exemplu, pe grupe de cate 2 sau 3 simboluri). In cazul codarii pe grupe de cate 2 simboluri, lungimea medie este:
![]()
iar lungimea medie pe simbol al sursei primare
![]()
este mai mica decat lungimea medie pe simbol din cazul codarii simbol cu simbol, conform primei teoreme a lui Shannon. Analog, in cazul codarii pe blocuri de simboluri de lungime 3.
3.Intrebari
1) Care sunt proprietatile codurilor obtinute prin algoritmul Huffman?
Codurile obtinute au lungimea medie a cuvantului de cod cea mai mica posibila a fi obtinuta printr-o metoda de codare.
2) Care sunt particularitatile algoritmului de codare Hufman binara/ternara?
Daca p(uj)>p(
3) Care tip de codare (simbol cu simbol, pe grupe de cate 2 simboluri) este mai eficient si de ce?
Codarea pe grupe de
simboluri este mai eficienta decat codarea simbol cu simbol, conform primei
teoreme a lui
4) Codarea Huffman binara/ternara poate duce la obtinerea unui cod absolut optimal?
Da, daca probabilitatile simbolurilor reunite, selectate la fiecare restrangere sunt egale, se obtine un cod absolut optimal.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








