
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Polarizarea de orientare a dielectricilor |
Polarizarea de orientare a dielectricilor
Polarizarea de orientare a dielectricilor
1. Modelul teoretic al dielectricilor cu polarizare de orientare si pierderi prin conductie
In absenta campului electric exterior momentele electrice elementare sunt distribuite aleatoriu, iar din punct de vedere macroscopic polarizatia este nula.
In prezenta unui camp electric exterior momentele electrice tind sa se orienteze in directia campului, iar polarizatia temporara este diferita de zero.
Modelul teoretic simplificat presupune doua stari stabile ale dipolilor: A si B, in care momentele electrice au aceasi directie cu a campului electric aplicat, dar sensuri opuse. Aceasta ipoteza nu exclude posibilitatea existentei unor stari diferite de starile A si B, doar ca aceste stari sunt presupuse mai putin probabile.
In fig.1.11 sunt reprezentate diagramele electrice corespunzatoare diferitelor stari, in absenta sau in prezenta campului electric exterior. In absenta acestuia, cele 2 stari sunt egal probabile, ele fiind separate printr-o bariera de potential Wo. Numarul de momente electrice din starea A este egal cu cel corespunzator starii B, in momentul initial, cand se aplica campul exterior, sau:
NA(0)=NB(0)=N/2 (1.48)
unde N reprezinta numarul total de stari A si B.
In prezenta campului electric exterior, cu orientare identica cu cea a momentelor din starea B, bariera de potential se micsoreaza cu We, favorizand tranzitiile momentelor electrice din starea A in starea B. Energia We reprezinta lucru mecanic efectuat de camp pentru a modifica orientarea momentului electric din starea A in starea B. Astfel, numarul momentelor din starea B va fi superior celui corespunzator starii A, sau:
![]() (1.49)
(1.49)
inegalitatea fiind cu atat mai pronuntata, cu cat intensitatea campului electric este mai ridicata.
Aplicand sistemului de momente electrice elementare statistica Boltzmann,
rezulta ca diferenta ![]() variaza
exponential cu timpul [Cat].
variaza
exponential cu timpul [Cat].
Polarizabilitatea sistemului de momente electrice variaza in timp proportional cu aceasta diferenta, conform unei relatii de forma:
![]() , (1.50)
, (1.50)
unde: ![]() este polarizabilitatea
la momentul initial, iar
este polarizabilitatea
la momentul initial, iar ![]() este constanta de
relaxare.
este constanta de
relaxare.
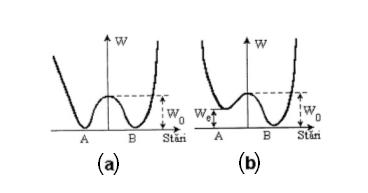
fig.1.11 Relieful de potential pentru un dielectric cu 2 stari stabile:
(a) - fara camp electric exterior; (b) - in prezenta campului
electric exterior cu orientare dipolara. [Cat]
|
Introducand relatia (1.50) in relatia (1.28), care se aplica si dielectricilor cu polarizare de orientare, se obtine:
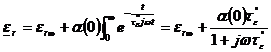 , (1.51)
, (1.51)
Prin identificare cu relatia (1.15), pentru un dielectric fara pierderi prin conductie rezulta:
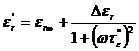 , (1.52)
, (1.52)
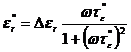 , (1.53)
, (1.53)
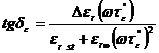 , (1.54)
, (1.54)
unde:![]() .
.
Pentru un dielectric cu pierderi prin conductie, relatia (1.53) se completeaza cu valoarea corespunzatoare pierderilor prin conductie data de relatia (1.46). Astfel, expresiile componentelor permitivitatii relative complexe si tangentei unghiului de pierderi, sunt de forma:
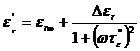 , (1.55)
, (1.55)
![]() , (1.56)
, (1.56)
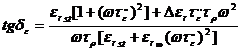 , (1.57)
, (1.57)
Pe baza relatiilor (1.52) si (1.57), verificate experimental, rezulta schemele echivalente ale condensatoarelor cu si fara pierderi prin conductie, reprezentate in fig.1.12.
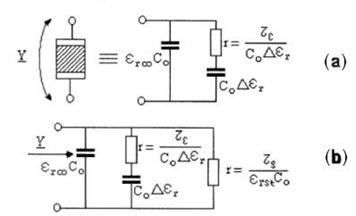
fig.1.12 Schema echivalenta a condensatorului cu dielectric cu polarizare de orientare:
(a) fara pierderi prin conductie si (b) cu pierderi prin conductie. [Cat]
2. Dependenta de frecventa si temperatura a permitivitatii relative complexe pentru dielectricii cu polarizare de orientare si pierderi prin conductie
Din diagramele reprezentate in fig.1.13, stabilite pe baza relatiilor
(1.55), (1.57), se observa ca la temperatura constanta,
permitivitatea reala descreste monoton cu frecventa,
datorita inertiei orientarii momentelor elementare atunci cand
frecventa creste. La frecvente ridicate, dielectricul are
permitivitate reala ![]() , datorata exclusiv polarizarii de deplasare
electronica.
, datorata exclusiv polarizarii de deplasare
electronica.
Tangenta unghiului de pierderi este puternic dependenta de frecventa. Primul maxim corespunde regimului stationar (ω=0) si este datorat pierderilor prin conductie, iar al doilea maxim este datorat pierderilor prin polarizare.
Permitivitatea reala in regim stationar scade pronuntat cu
temperatura dupa legea Curie: ![]() . (1.58)
. (1.58)
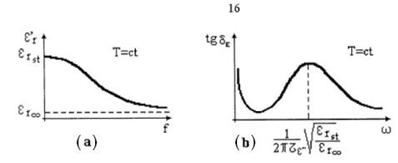
fig.1.13 Dependenta de frecventa la temperatura constanta a permitivitatii reale si a tangentei unghiului de pierderi pentru dielectricii cu polarizare de orientare si pierderi prin conductie. [Cat]
In figurile (1.14) si (1.15) sunt reprezentate diagramele de variatie ale permitivitatii reale si tangentei unghiului de pierderi cu frecventa si temperatura.
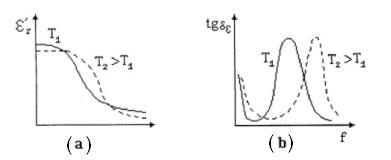
fig.1.14 Dependenta de frecventa la doua temperaturi diferite a permitivitatii reale si a tangentei unghiului de pierderi, pentru dielectricii cu polarizare de orientare si pierderi prin conductie. [Cat]
La frecvente mici si medii, permitivitatea reala, prezinta o puternica dependenta de temperatura, iar la frecvente ridicate, devine preponderenta contributia polarizarii de deplasare electronica, care se modifica nesemnificativ cu temperatura. Intersectiile caracteristicilor pentru diferite temperaturi presupun o dependenta neunivoca. Astfel, marimile la un moment dat, depind de evolutia anterioara, comportarea dielectricului fiind diferita la cresterea, respectiv scaderea temperaturii.
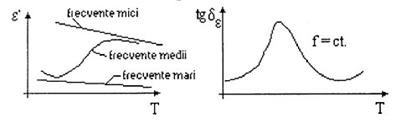
fig.1.15 Dependenta de temperatura la frecventa constanta a permitivitatii reale si a tangentei unghiului de pierderi pentru dielectricii cu polarizare de orientare si pierderi prin conductie. [Cat]
Tangenta unghiului de pierderi prezinta un maxim datorat pierderilor prin polarizare si creste exponential la temperaturi ridicate, datorita pierderilor prin conductie.
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Documente online pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








