
| Biologie | Botanica | Chimie | Didactica | Fizica | Geografie |
| Gradinita | Literatura | Matematica |
Fizica
|
|
Qdidactic » didactica & scoala » fizica Forta lui Arhimede - forta de impingere de jos in sus in lichide - principiul lui Arhimede |
Forta lui Arhimede - forta de impingere de jos in sus in lichide - principiul lui Arhimede
(Forta lui Arhimede)
Principiul lui Arhimede
Corpurile cufundate in apa par mai usoare decat in aer. Daca se
introduce in apa un corp usor si apoi i se da drumul, acesta revine la
suprafata apei cu mare viteza si pluteste. Forta care
actioneaza asupra corpului impingandu-l in sus se numeste forta lui Arhimede.
Cauza impingerii de jos in sus o constituie presiunea hidrostatica a apei, care
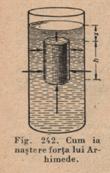
are alta valoare la fiecare adancime. Sa presupunem ca la adancimea ![]() in interiorul unui
lichid cu greutatea specifica
in interiorul unui
lichid cu greutatea specifica ![]() se gaseste un corp
cilindric avand inaltimea
se gaseste un corp
cilindric avand inaltimea ![]() si sectiunea S
(fig. 242). Pe fata superioara a corpului actioneaza o forta
si sectiunea S
(fig. 242). Pe fata superioara a corpului actioneaza o forta ![]() reprezentata
printr-o sageata indreptata in jos, iar pe fata inferioara o fota
reprezentata
printr-o sageata indreptata in jos, iar pe fata inferioara o fota ![]() reprezentata
printr-o sageata in dreapata sus. Fortele care actioneaza la aceeasi inaltime
asupra fetei laterale a corpului au rezultanta nula. In total ramane o forta
actionand in sus de marime
reprezentata
printr-o sageata in dreapata sus. Fortele care actioneaza la aceeasi inaltime
asupra fetei laterale a corpului au rezultanta nula. In total ramane o forta
actionand in sus de marime ![]() , care este tocmai forta lui Arhimede.
, care este tocmai forta lui Arhimede.
Intrucat ![]() este
volumul corpului, rezulta:
este
volumul corpului, rezulta:
forta lui Arhimede=volumul·greutatea specifica:
![]() [kgf].
[kgf].
Expresia de mai sus reprezinta formularea matematica a principiului lui Arhimede: forta lui Arhimede este egala cu greutatea cantitatii de apa dezlocuite de corp.
Deoarece asctioneaza in sens contrar greutatii corpului, forta lui Arhimede produce totdeauna o micsorare a greutatii.
Valoarea fortei lui Arhimede=piererea de greutate.
Aceasta pierdere de greutate depinde, prin urmare, numai de volumul corpului cufundat, respectiv de cantitatea de apa dezlocuita, nu si de greutatea sa. Un bloc de plumb cufundat cu acelasi volum ca si o bucata de lemn este impins cu aceeasi forta A, ca si aceasta.
Daca G este greutatea proprie a corpului si A este forta lui Arhimede, in functrie de valoarea uneia fata de cealalta pot exista trei situatii:
1. G>A: corpul se cufunda cu greutate micsorata
2. G=A: corpul pluteste
3. G<A: corpul se ridica la suprafata
Micsorarea greutatii corpurilor in lichide
Am stabilit ca greutatea unui corp complet cufundat intr-un lichid se micsoreaza cu valoarea fortei lui Arhimede. Dat fiind ca in apa curata cu greutatea specifica de 1gf/cm3 aceasta impingere este numeric egala cu volumul apei dezlocuite, rezulta o posibilitate comoda de determinare a greutatii specifice a obiectelor mici. Cu ajutorul unei balante hidrostatice se afla mai intai greutatea corpului in aer, G, apoi se atarna corpul de un fir, introducandu-l in apa, si se afla greutatea lui redusa, G' (fig. 243). Rezulta:
greutatea
specifica=![]() [gf/cm3]
[gf/cm3]


Deoarece scaderea greutatii unui corp depinde de greutatea specifica a lichidului in care se cufunda, avem inca un mijloc de a determina foarte precis greutatea specifica a lichidelor.
De bratul balantei Mohr-Westphal (fig. 244) se suspenda printr-un fir de platina un mic corp plutitor de sticla. Daca se cufunda corpul in apa, echilibrul se strica. El poate fi restabilit printru-un carlig de sarma (calaret) atarnat la crestatura 10, adica greutatea specifica a lichidului este exact egala cu 1. Alte doua carlige egale cu 1/10, respectiv 1/100, din greutatea calaretului celui mare, servesc la echilibrare, daca greutatea specifica este diferita de 1. Pozitia calaretilor din fig. 245 indica, de exemplu, o greutate specifica de 1.035. Inainte de intrebuintare, balanta trebuie sa fie adusa mai intai in stare de echilibru cu apa crata. Deoarece apa nu are greutate sfecifica 1 la temperatura camerei, trebuie facuta corectia corespunzatoare, cu ajutorul unei table de densitati.

Plutirea
Cand forta lui Arhimede este mai mare decat greutatea corpului acesta se deplaseaza in sus pana ce la suprafat se stabilieste echilibrul intre cele doua forte. Atunci corpul pluteste. Prin urmare, daca o bucata de lemn care pluteste in apa are greutatea in aer are 650 kgf, rezulta ca volumul partii sale cufundate trebuie sa fie de 0,65 m3.
Echilibrul de plutire: cand un corp pluteste in apa curata, greutatea apei dezlocuite este egala cu greutatea proprie a corpului.
Acest fenomen poate fi dovedit usor. Se umple cu apa un vas de preaplin. Daca se introduce apoi in el un corp plutitor, se scurge din vas exact atata apa cat de greu este corpul.
In
cazul unui lichid oarecare cu greutate specifica ![]() , daca se noteaza cu
, daca se noteaza cu ![]() volumul partii
cufundate a corpului, se poate scrie ultima lege si sub forma
volumul partii
cufundate a corpului, se poate scrie ultima lege si sub forma ![]() , de unde:
, de unde:
|
![]()
cu alte cuvinte:
volumul cufundat / volumul total = greutatea specifica a corpului / greutatea specifica a lichidului
Cu ajutorul acestei relatii se poate determina ce fractiune dintr-un corp plutitor iese afara din lichid.
Partea care iese afara poate fi facuta sa intre complet in apa prin adaugarea unei greutati suplimentare. Volumul acestei parti reprezinta deci forta portanta a unui obiect plutitor, pe care se poate conta in caz de cufundare completa a obiectului.
Pentru ca o pluta sa suporte un om cu greutatea de 80 kgf, partea ei care se gaseste deasupra apei trebuie sa reprezinte cel putin 80 l. O marime a fortei lui Arhimede peste aceasta limita nu este posibila, afara de cazul cand incarcatura s-ar cufunda si ea impreuna cu pluta si ar contribui astfel la cresterea fortei lui Arhimede.
Pozitia de plutire
Echilibrul de plutire este foarte sensibil la perturbari. Din cauza mobilitatii mari a apei, echilibrul instabil este absolut imposibil. Prin urmare, un corp nu poate fi mentinut in stare de plutire in orice pozitie, ci se roteste singur si ocupa pozitia corecta, stabila, de plutire. Pentru aceasta pozitie, au importanta covarsitoare doua puncte:
1. Centrul de greutate al corpului (punctul C de aplicatie a greutatii). El are o pozitie fixa in corp.
2. Centrul de presiune (punctul A de aplicatie a fortei lui Arhimede), care este centrul de greutate al lichidului dezlocuit. Elisi schimba pozitia dupa marimea si forma partii cufundate.
Daca centrul de greutate C se gaseste sub centrul de presiune A, pozitia de plutire este in oricare caz stabila. O mica rasucire din aceasta pozitie face sa apara un cuplu de forte, care roteste corpul inapoi pana in momentul devine din nou egal cu zero.
Linia verticala care uneste C cu A este axa de plutire a corpului.
Daca C se gaseste exact deasupra lui A, momentul cuplului este tot egal cu zero, dar se disting doua cazuri. Rotind corpul putin, il scoatem prin pozitia de echilibru. Daca linia de actiune care trece prin noul centru de presiune A' intersecteaza vechea axa de plutire sub C, ia nastere un moment care rastoarna corpul (fig. 246). Prin urmare, echilibrul era nestabil. Daca acest punct de intersectie se gaseste deasupra lui C, corpul revine la vechea sa pozitie: echilibrul era stabil (fig. 247). Punctul de intersectie a liniei de actiune a fortei care trece prin A' cu axa de plutire se numeste metacentru.
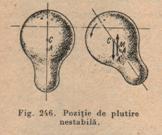

Pozitia de plutire a unui corp este stabila cand metacentrul se gaseste deasupra centrului sau de greutate.
In general, un obiect pluteste cu atat mai stabil, cu cat centrul sau de greutate se gasete mai jos. Iahturile cu panze au chila grea, iar in caz de pericol de naufragiu trebuie sa se dea jos catargele.
Pentru determinarea pozitiei de plutire a vaselor, a clopotelor gazometrelor si a altor constructii tehnice, de cele mai multe ori sant necesare calcule mai complicate.
Un exemplu simplu in acest sens il constituie determinarea rapida a greutatii specifice a lichidelor, cu ajutorul densimetrelor (aerometre). Ele sunt niste tuburi de sticla lestate, a caror parte superioara iese deasupra nivelului lichidului si au o scala gradata corespunzatoare scopului experientei. In functie de greutatea specifica a lichidului, ele se cufunda mai mult sau mai putin in acesta (fig. 248). Sensibilitatea densimetrelor este cu atat mai mare cu cat gatul care iese afara din lichid este mai subtire in raport cu partea cufundata. Densimetrele sunt foarte raspandite ca aparate de verificat densitatea acizilor, ca lactometre, alcoolmetre, zaharometre pentru determinarea continutului in zahar al solutiilor.

Presiunea atmosferica
Intr-un corp gazos, fenomenele se petrec oarecum ca intr-o aglomeratie de oameni. Moleculele in miscare se ciocnesc mereu intre ele si se izbesc de peretii vasului in care sunt inchise. Desi o molecula are o masa infima, numarul lor enorm da o forta considerabila pe fiecare unitate de suprafata (s-a putut stabili ca 1 cm3 de gaz contine, in conditii obisnuite, 27 milioane de molecule).
De aici rezulta ca si aerul obisnuit din atmosfera terestra trebuie sa aiba o anumita presiune. Daca se umple complet cu apa un pahar cu buza neteda si apoi se pune deasupra lui o foaie de hartie (fig. 252), apasand usor hartia cu palma si intorcand paharul cu gura in jos, chiar daca luam mana de pe hartie nu curge nici o picatura de apa din pahar. Hartia este mentinuta de presiunea atmosferica.



In loc de apa, savantul italian Torricelli (1643) a folosit mercur (fig. 253). Se umple cu mercur un tub inchis la un capat; celalalt capat se astupa cu degetul si se descopera din nou orificiul dupa ce s-a intors tubul cu gura in jos si s-a introdus intr-un vas larg, de asemenea umplut cu mercur. Lichidul din tub coboara atunci la un anumit nivel si lasa in capatul de sus al tubului un spatiu far aer. Inaltimea coloanei de mercur, masurata intre nivelul mercurului din vas si limita superioara a meniscului din tub, da vcaloarea presiunii aerului in mediul inconjurator. Aceasta valoare se indica in milimetri de coloana de mercur. In cinstea lui Torricelli s-a adoptat notatia:
1mm coloana de mercur=1 torr
Presiunea atmosferica nu este o marime constanta. Ea este in permanenta supusa oscilatiilor, in functie de altitudine si de starea vremii. La nivelul marii si la o temperatura medie anuala de 15°C exista:
presiunea normala (atmosfera standard)=760 torr
La circa 5500 m altitudine,
presiunea atmosferica are jumatate din valoarea normala, la o altitudine dubla
ea are numai circa ¼. Ele mai inalte aurore boreale au fost
observate la atitudine de 1000 km, ceeace dovedeste ca si acolo trebuie sa mai
existe urme de aer. Pentru calculul presiunii atmosferice
B la diferite altitudini ![]() s-a stabilit
s-a stabilit
formula internationala a altitudinii: 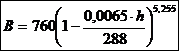 [torr]
[torr]
Aceasta formula este valabila pana la 11000 m.
Valoarea presiunii atmosferice in alte sisteme de unitati
Sa presupunem ca sectiunea coloanei de mercur este de 1 cm2. Prin uramre, daca inaltimea coloanei este de 76 cm, iar greutatea specifica a mercurului este de 13,595 gf/cm3, presiunea coloanei are valoarea 76 cm·13,595 gf/cm3=1033 gf/cm2. Aceasta forta raportata la un centrimetru patrat da tocmai expresia presiunii deja cunoscuta de noi:
760 torr=1033 gf/cm2=1,033 kgf/cm2=1,033 at=1 atm
Asadar, presiunea atmosferica normala este putin mai mare decat o atmosfera tehnica. Ea se numeste atmosfera fizica (1 atm).
Daca nu simtim de loc efectul presiunii aerului, motivul este simplu: corpul nostru nu este supus la presiune numai din exterior ci estesupus la o presiune egala si din interior, astfel ca efectul se anuleaza complet.
Transformarea inversa ne da relatia:
1 at=735,6 torr
In meteorologie, presiunea atmosferica se da in minibari (mbar), adica in sistemul CGS unde 1 gf=981 dyn. Presiunii atmosferice normale ii corespund deci 1033 gf/cm2·981 dyn/gf=1013250 dyn/cm2. Celelalte unitati sunt:
106 dyn/cm2=1 bar
103 dyn/cm2=1 milibar (mbar)
1 dyn/cm2=1 microbar (![]() bar sau barye)
bar sau barye)
Prin urmare:
760 torr=1013,25 milibar (mbar)
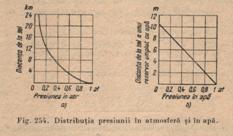
Distributia presiunii in atmosfera
este fundamental diferita de distributia presiunii in apa, unde (canad
abstractie de compresibilitatea redusa) se intalneste la toate adancimile aceesi densitate (fig. 254). Daca insa s-ar
presupune ca si densitatea aerului este constanta, inaltimea totala a
atmosferei s-ar calcula in modul urmator: 1 m3 de aer cantareste
1,293 kgf, iar presiunea aerului este de 10330 kgf pe fiecare metru patrat;
aceasta corespunde la o inaltime totala de ![]() m
m![]() 8000 m. Pentru fiecare scadere a
presiunii cu 1 torr, rezulta o diferenta de inaltime de
8000 m. Pentru fiecare scadere a
presiunii cu 1 torr, rezulta o diferenta de inaltime de ![]() m
m![]() 10,5 m. Deoarece, insa, dupa cum s-a
spus, invelisul de aer al Pamantului nu este omogen, se poate folosi aceasta
valoare numai in limitele unei diferente mici de naltime, unde scaderea
relativa de densitate este inca destul de redusa.
10,5 m. Deoarece, insa, dupa cum s-a
spus, invelisul de aer al Pamantului nu este omogen, se poate folosi aceasta
valoare numai in limitele unei diferente mici de naltime, unde scaderea
relativa de densitate este inca destul de redusa.
La fiecare crestere a altitudinii cu 10,5 m presiunea aerului scade cu cate 1 torr (valabil numai pentru diferente mici de altitudine).
Barometrul
Inasasi instalatia din experienta lui Torricelli constituie un barometru simplu. Pentru economisirea mercurului, trebuie sa construiesc mai stramte si se curbeaza in partea de jos in forma de U, obtinandu-se un barometru cu sifon (fig. 256). Citirea se face totdeauna la nivelul varfului meniscului.


Deoarece volumul mercurului se
dilata la o incalzire la 1° cu factorul 0,000181, trebuie sa se reduca lungimea
citita ![]() a coloanei de mercur,
la 0°C
a coloanei de mercur,
la 0°C
![]()
ina
care ![]() reprezinta temperatura.
reprezinta temperatura.
La masuratorile foarte precise, trebuie sa se tina seama si de capilaritate, de dilatarea scalei.
O citire mai clara se poate efecta cu contrabarometrul, care transmite miscarea nivelului mercurului din ramura scurta a tubului la un fir de lichid (toluen colorat).
Mai comod, desi mai putin precis, este barometrul metalic sau aneroid (fig. 257). El este o cutie de tabla din care s-a scos aerul, cutie ce poate fi comprimata mai mult sau mai putin de catre presiunea variabila a aerului si poate transmite miscarea la un ac indicator cu scala.
Barografele (fig. 258) inregistreaza variatia presiunii aerului, prin intermediul unui varf muiat in cerneala, care traseaza curba respectiva pe o banda de hartie infasurata pe un tambur rotativ. Curba astgel obtinuta reda modul de variatie a presiunii aerului in cursul unei zile intregi.

Bibliografie
"FIZICA pentru tehnicieni", vol. I, "Mecanica corpurilor solide. Mecanica lichidelor si a gazelor" - Helmut Lindner - Editura Tehnica, Bucuresti, 1960
| Contact |- ia legatura cu noi -| | |
| Adauga document |- pune-ti documente online -| | |
| Termeni & conditii de utilizare |- politica de cookies si de confidentialitate -| | |
| Copyright © |- 2025 - Toate drepturile rezervate -| |
|
|
|||
|
|||
Lucrari pe aceeasi tema | |||
|
| |||
|
|||
|
|
|||








